I can reproduce this issue.
The option 'counts' simply selects different ways to store the graph internally (in graph-tool). Whe reason why we end up with different results is that graph-tool's algorithm is stochastic and can end up in different local minima (of the description length) if starting from different initial conditions. While I set a seed for graph-tool's random number generator, I assume that the different representations of the graph lead to different selection of random numbers. Therefore we end up with different solutions.
In this dataset, there are in fact two solutions with similarly small description length (corresponding roughly to the two cases you describe above). The seemingly 'unordered' solution is thus not necessarily an artifact. With slightly larger datasets, I assume that it will be less liklely to end up in such a local minimum.

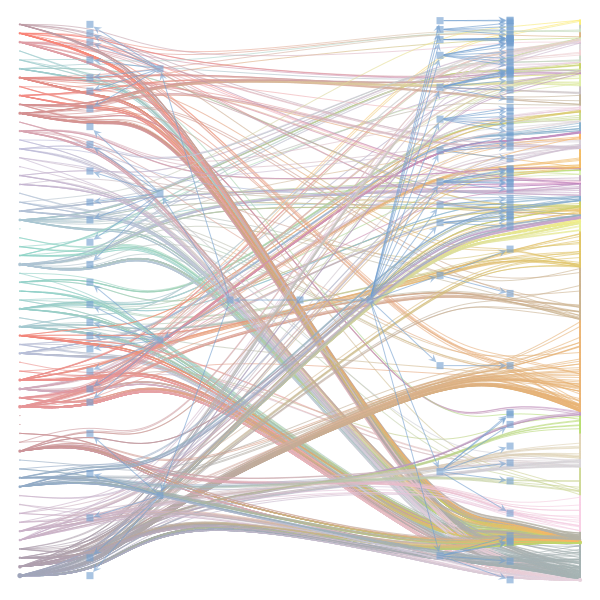
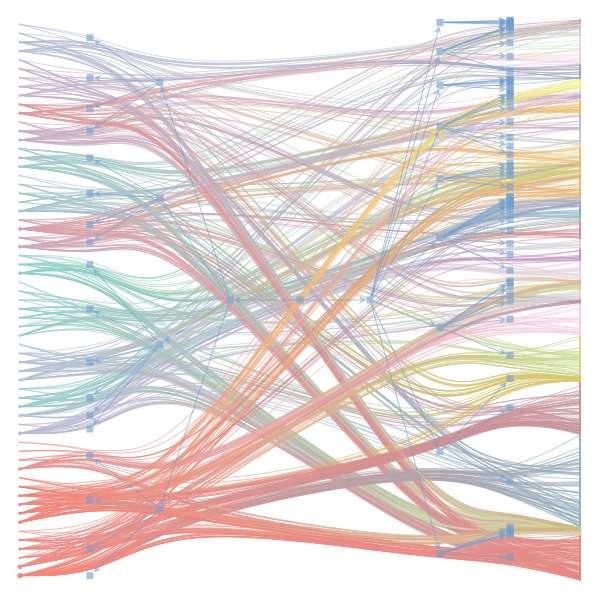
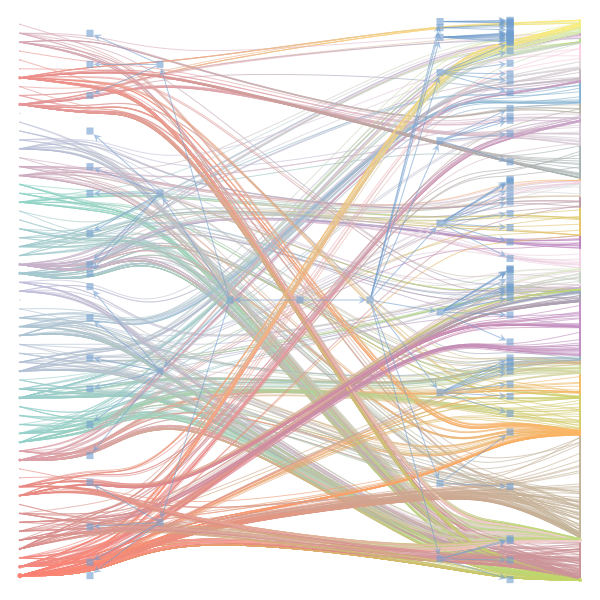
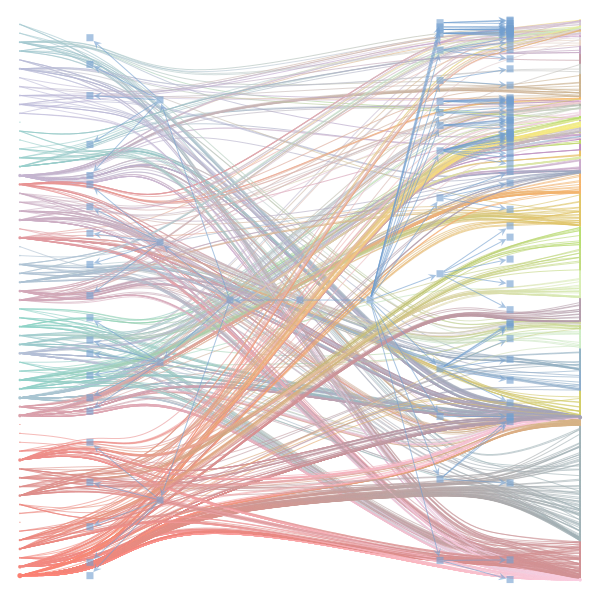
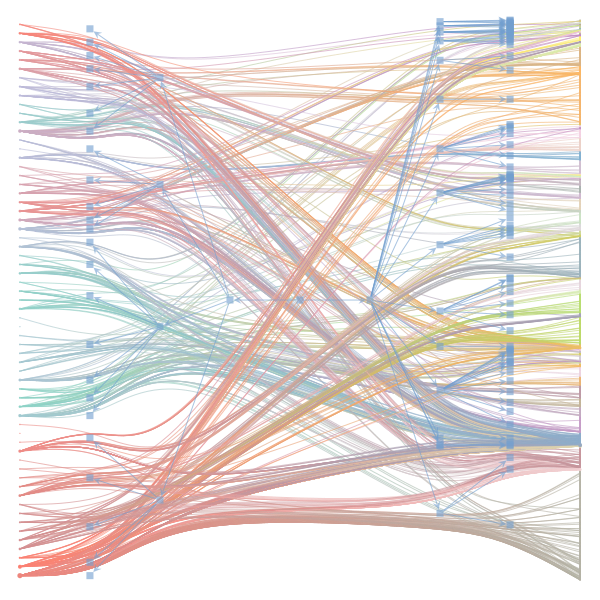
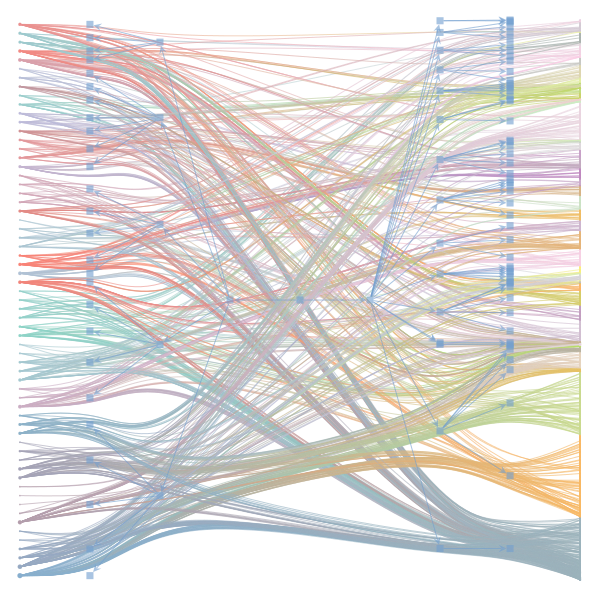
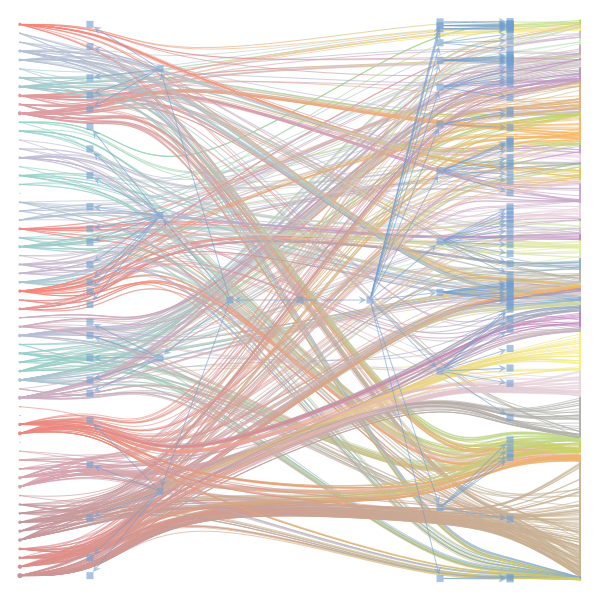
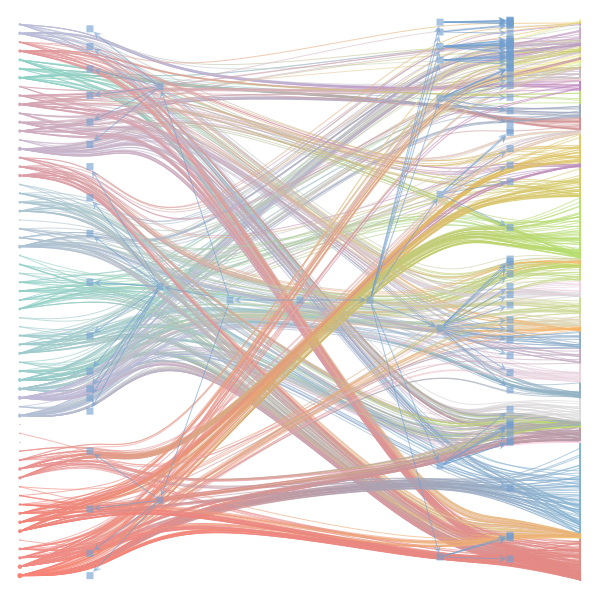
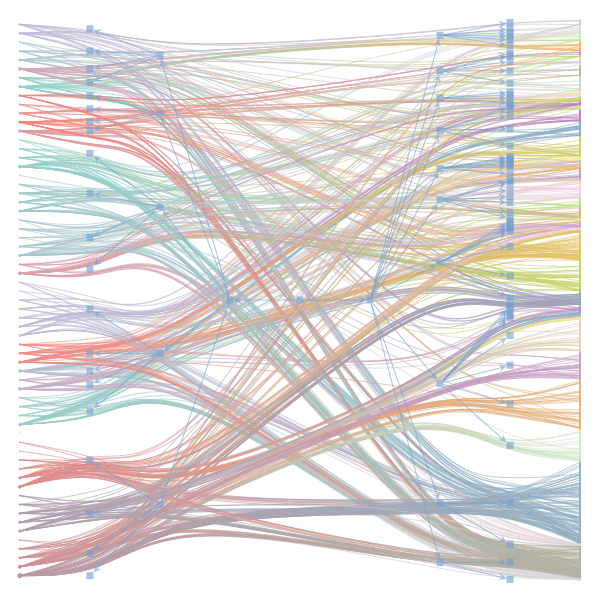



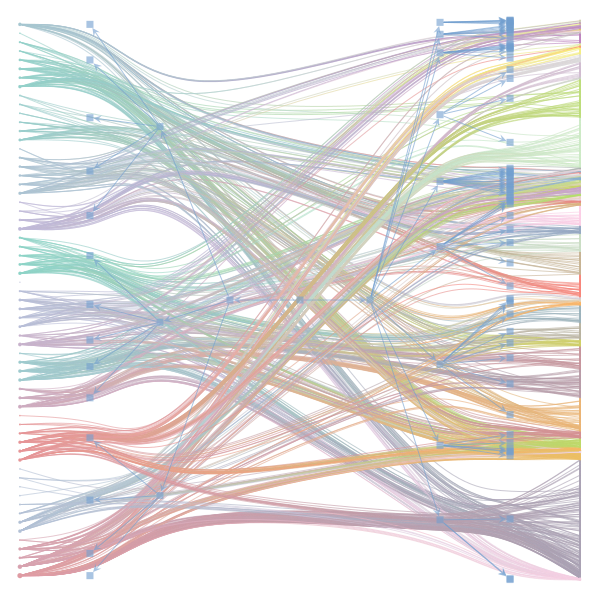

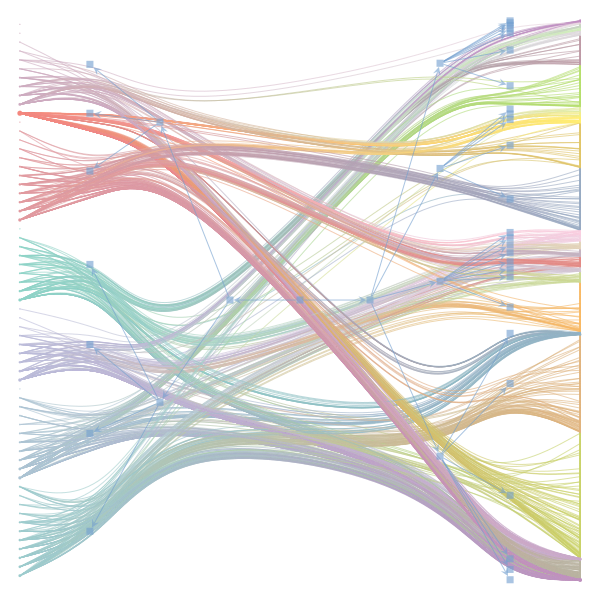


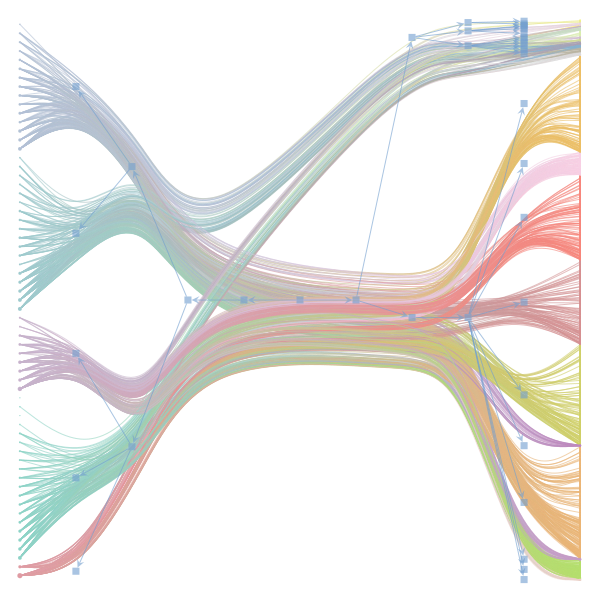
The Jupyter notebook uses
make_graphwith the implicitcounts=True. The published plot looks something like this:but with
counts=TrueI can only get plots likeIs counts=True working for inference but not for plotting? Or is it broken for inference too?