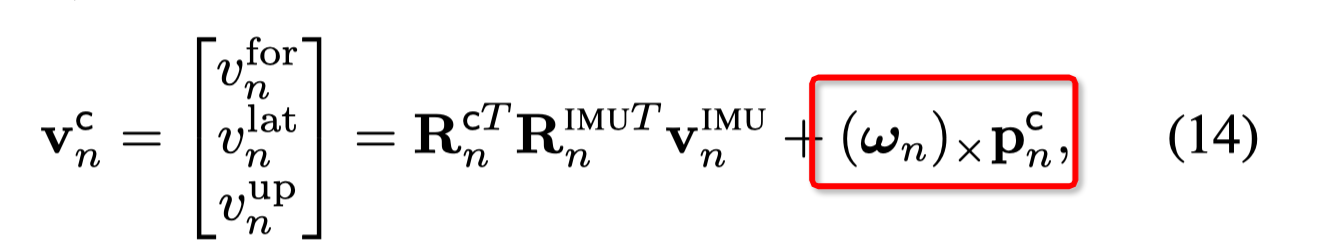@milkcoffee365, it seems suspicious indeed because we know that
Thus, I would expect a subtraction instead of an addition. Line 219 seems fine due to the transformations that happen in previous lines.
Open milkcoffee365 opened 2 years ago
@milkcoffee365, it seems suspicious indeed because we know that
Thus, I would expect a subtraction instead of an addition. Line 219 seems fine due to the transformations that happen in previous lines.
@milkcoffee365 Was this ever sorted out?
@milkcoffee365 , @paaraujo , @scott81321
First say my conclusion, line 221 should be:
v_body += Rot_c_i.T.dot(self.skew(u[:3] - b_omega).dot(t_c_i))
in other words, self.skew(u[:3] - b_omega).dot(t_c_i) is the velocity in the IMU-frame, since both angular velocity u[:3] and t_c_i are elements resolved in the IMU-frame, we still need to transform it into vehicle-frame.
Below are some derivations:
Assume R_c_n and p_c_n are the rotation and displacement of vehicle-frame relative to imu-frame, which are RESOLVED in the imu-frame at time instant n.
p_c_n is vector starting from the origin of imu-frame and ending at the origin of the vehicle-frame, and this vector is resolved in the imu-frame.
To make derivation easy, let's reference to the world-frame
When referenced to the world-frame, The IMU-frame's velocity is v_IMU_n, IMU-frame's angular velocity is R_imu_n * w_n,
Then based on the extrinsic between vehicle and imu, the vehicle-frame's velocity v in the world frame would be: v = v_IMU_n + (R_imu_n w_n)x r, here r = R_imu_n p_c_n, in which we translate the imu-frame referenced lever arm p_c_n into a world-frame referenced one.
Then the vehicle-frame's velocity in the vehicle-frame would be: v_c_n = transpose(R_c_n) transpose(R_imu_n) v = transpose(R_c_n) transpose(R_imu_n) v_IMU_n + transpose(R_c_n) * (w_n x p_c_n)
In the above equation derivation, we use the property of skew(Rw) = Rskew(w)transpose(R) and w_n x p_c_n = skew(w_n) p_c_n. skew(.) is used to transform a vector into a skew symmetric matrix.
So in summary, in the equation (14), the authors missed the multiplication of matrix transpose(R_c_n) before (w_n x p_c_n)
Fyi, the arxiv preprint is different from the published IEEE version where this is fixed. The measurement Jacobians are also different.
@vkorotkine Are you saying their published IEEE paper has the correction mentioned by @robocar2018 ? If so, please show us clips of the where the IEEE paper differs from the arxiv version. I cannot access the IEEE paper, only the HAL and arxiv versions. I would be surprised that the code would not implement exactly what is presumably in the IEEE paper including later fixes (?)
@vkorotkine , thanks for your reminder. @scott81321 , Vkorotkine is correct, the IEEE version fixed the error. Below is a link for the IEEE version, please see the equation (14), multiplication of matrix transpose(R_c_n) is applied before (w_n x p_c_n). https://www.researchgate.net/publication/339920913_AI-IMU_Dead-Reckoning
Furthermore, the measurement matrix H in the IEEE version is also fixed.
@vkorotkine You're right. I see the change in the paper in terms of bracketing. This is cause for concern because it means ai-imu-dr code, at least for that eq. 14, does not match the paper. Mind you, this fix does not solve my current test problem. That 2nd term is a small contribution, for my case anyway.
Now, you mention changes in the Jacobians. I see a discrepancy for the 'B' term below eq. 37 pertaining to H_n in eq. 37. If I am not mistaken, in the code in utils_numpy_filter, that's:
H_v_imu = Rot_c_i.T.dot(self.skew(v_imu))The 'B' in the paper looks rather different. There is an additional term. It looks like here as well, the code does not match the IEEE paper.
Anything else?
@scott81321 , here is the result of my derivation for the H H = A[0, R_IMU_T_n, 0, skew(p_c_n), 0, B, C], with A the same as paper's definition. B = skew( R_IMU_T_n * v_IMU_n + (w_imu_n - b_w_n) x p_c_n ) C = skew(w_imu_n - b_w_n)
Basically, B in the IEEE paper's looks to be a typo and hopefully should be the same as my derivation.
And both skew(p_c_n) and C have a sign difference compared to the IEEE paper.
It looks like the code is not updated, since
H_v_imu = Rot_c_i.T.dot(self.skew(v_imu))
only includes one item, and the skew( (w_imu_n - b_w_n) x p_c_n ) is missing from the code.
where b_w_n is the estimated gyro bias, and p_c_n is the lever arm between imu-frame and vehicle-frame, resolved in the imu-frame. w_imu_n is the gyro reading
@robocar2018 OMG so even the IEEE paper has an error? Any other discrepancies you noticed? @vkorotkine mentioned Jacobians i.e. in the plural.
@scott81321 , for the IEEE paper, at least we can see the common extrinsic matrix is extracted out for the H matrix, which is reflected inside the matrix A. While for the arxiv preprint, we could see the extrinsic matrix is missing in the matrix A. As for the matrix B, IEEE paper looks to be a typo, since the following expression does not make sense,

From the updated equation (14),
 we can compute the Jacobian with respect to the extrinsic matrix R_c_n based on some formula.
we can compute the Jacobian with respect to the extrinsic matrix R_c_n based on some formula.
@robocar2018 I gather b_w_n must be 'b_omega' in the code, right? 'C' is 'Omega' in the code 't_c_i' is 'p_n_c' as you call it. In the code, 'w' is u[:3] and you always find b_omega subtracted from it i.e. u[:3] - b_omega. u[:3] is w_IMU and w_n = w_IMU - b_w_n. If I did this right, the code should be:
Omega = self.skew(u[:3] - b_omega)
# Jacobian w.r.t. car frame H_v_imu is 'B' in paper
H_v_imu = Rot_c_i.T.dot(self.skew(v_imu))
H_v_imu += self.skew(Omega.dot(t_c_i))correct?
@scott81321 , yes you are right. Also I added some comments in my previous reply.
H_v_imu += self.skew(Omega.dot(t_c_i))@scott81321 , below is my updated measurement Jacobian matrix H in the code. Please let me know if you have any questions, thanks. Basically in the original code, I found the authors forgot to multiply the common extrinsic matrix (Rot_c_i.T) for some submatrices in the H.
def update(self, Rot, v, p, b_omega, b_acc, Rot_c_i, t_c_i, P, u, i, measurement_cov):
Omega = self.skew(u[:3] - b_omega) # skew of angular velocity
# orientation of body frame
Rot_body = Rot.dot(Rot_c_i)
# velocity in body frame in the imu axis
v_imu = Rot.T.dot(v)
v_body = Rot_c_i.T.dot(v_imu + Omega.dot(t_c_i)) # velocity in body frame in the vehicle axis
# Jacobian w.r.t. car frame
H_v_imu = self.skew(v_imu + Omega.dot(t_c_i))
H_t_c_i = self.skew(t_c_i)
HH = np.zeros((3, self.P_dim)) # HH is a 3x21 matrix
HH[:, 3:6] = Rot_body.T
HH[:, 9:12] = Rot_c_i.T.dot(H_t_c_i)
HH[:, 15:18] = Rot_c_i.T.dot(H_v_imu) # Jacobian of delta_imu_car_rotation_extrinsic
HH[:, 18:21] = Rot_c_i.T.dot(Omega) # Jacobian of delta__imu_car_translation_extrinsic
H = HH[1:] # extract the second and third rows from HH, which correspond to lateral and vertical speed components respectively.
r = - v_body[1:] # r is the residual between measurement, which is just difference between a 2x1 zero vector and v_body[1:],
# v_body[1] is the lateral speed, v_body[2] is the upward speed
R = np.diag(measurement_cov)
# Update the state and its covariance matrix
Rot_up, v_up, p_up, b_omega_up, b_acc_up, Rot_c_i_up, t_c_i_up, P_up = \
self.state_and_cov_update(Rot, v, p, b_omega, b_acc, Rot_c_i, t_c_i, P, H, r, R)
return Rot_up, v_up, p_up, b_omega_up, b_acc_up, Rot_c_i_up, t_c_i_up, P_up
@robocar2018 Thank you for all this. I have implemented this code and found that it did not fix the issue I faced concerning eq. 6. These extra terms in 'w' which involve the gyroscope readings are very very small. In my case, I have a gyro_z lasting for a while with a vehicle experiencing changing velocities. The algo fails here even with these corrections to the code. The Rotation matrix Rimu of eq. 6 degrades and when the vehicle comes to a dead stop, there is no gyro 'juice' to kickstart RImu out of its bad state of the rotation matrix creates spurious accelerations. The code has a 'normalize_rot' routine to deal with numerical error on the Rimu but it is not enough. Any suggestions?
@scott81321, I don't think this algorithm can work well when the vehicle stops, since we don't use those measurements that indicate the vehicle is in a static state (like ZUPT). When the vehicle stops, the gyro bias will cause Rotation matrix Rimu to drift, and which in turn will cause spurious accelerations as you discovered. So to test this algorithm, we need the vehicle to be in a non-static mode. To work well in a static state, we need some external sensors to tell us that the vehicle stops, so we could compute the bias of gyro by just averaging the gyro output and then compensate it.
Thanks for telling me. You're right. But here is an idea. If the vehicle is at a stop, what if one measured the mean gyro and mean accel for say a period of time, say a few seconds? During a full stop, I expect the noise to be Gaussian. The mean if accel_x,y and gyro_x,y,z should be zero (drift not withstanding) and accel_z should be registering gravity (using KITTI format with x as forward, y is left and z is up). On a flat surface pitch and roll are zero and I gather so would yaw during a full stop (?) I did some testing and although my notion is still dodgy, I found that I could detect near zero velocity for accel x,y below specific thresholds. A machine learning type approach would be better.
@scott81321, Yes, Looks like it can work. But I guess yaw would still drift in a longer term when the vehicle stops for a long time. Anyway, adding ZUPT feature would definitely improve this dead reckoning performance which lacks in the current open source code. By the way, can you make commit to the code base? If so, could you please commit this ZUPT feature (by tracking IMU) into the code? Thanks.
@robocar2018 Hello, in regards to your first question, if you mean committing code to ai-imu-dr, only Martin Brossard can commit and he has his own 'commitments' in industry. As for my own code, sorry but that is propriety though I can mention ideas.
@scott81321 , no problem. FYI: I just tried compared the Jacobian matrix H based on my derivation and the one from the IEEE paper on two data slices and observed smaller average position errors on my derived H (which is based on Fig 7 of the code).
@scott81321 THX. It makes sense. Please let us know if you find any other errors or discrepancies in the equations of the paper. In the meantime, my kludge of estimating if the velocity is below a threshold, say 0.15 m/s, based entirely on IMU accel data works surprisingly well. Thanks for the ZUPT heads up. Mind you, I still would like to resolve the degradation of the Rotation matrix before the algo reaches that critical point where the vehicle has stopped. When this happens, the angle between R*g and g seems to get worse. My yaw descends to about one but then remains level when it should gradually go to zero. I saw your recent issue. I am a bit puzzled. Surely the effect of the earth's radius is not felt over a range of a few meters?
Hello @robocar2018 Since you have gone to this trouble to re-derive the equations of Brossard's paper, could you please make them public? E.g. could you scan them and post them somehow?
A few questions to you (or anyone else who can answer), if I may:
1) In the paper, below eq. 11, it is said that "...the covariance matrix is updated through P_n+1 = FnPnFn^T + GnQnGn^T , (11) where Fn, Gn are Jacobian matrices of f(·) with respect to x_n and u_n". Some have read this and concluded that Fn is df/dx_n and Gn is df/du_n. I, for one, doubt this interpretation but can you say anything about this?
2) Do you have any info or knowledge about Gn? It seems to be rather unique in that I don't find it explicitly for the standard Kalman filter or even the extended version.
In utils_numpy_filter.py. The body velocity computation seems wrong?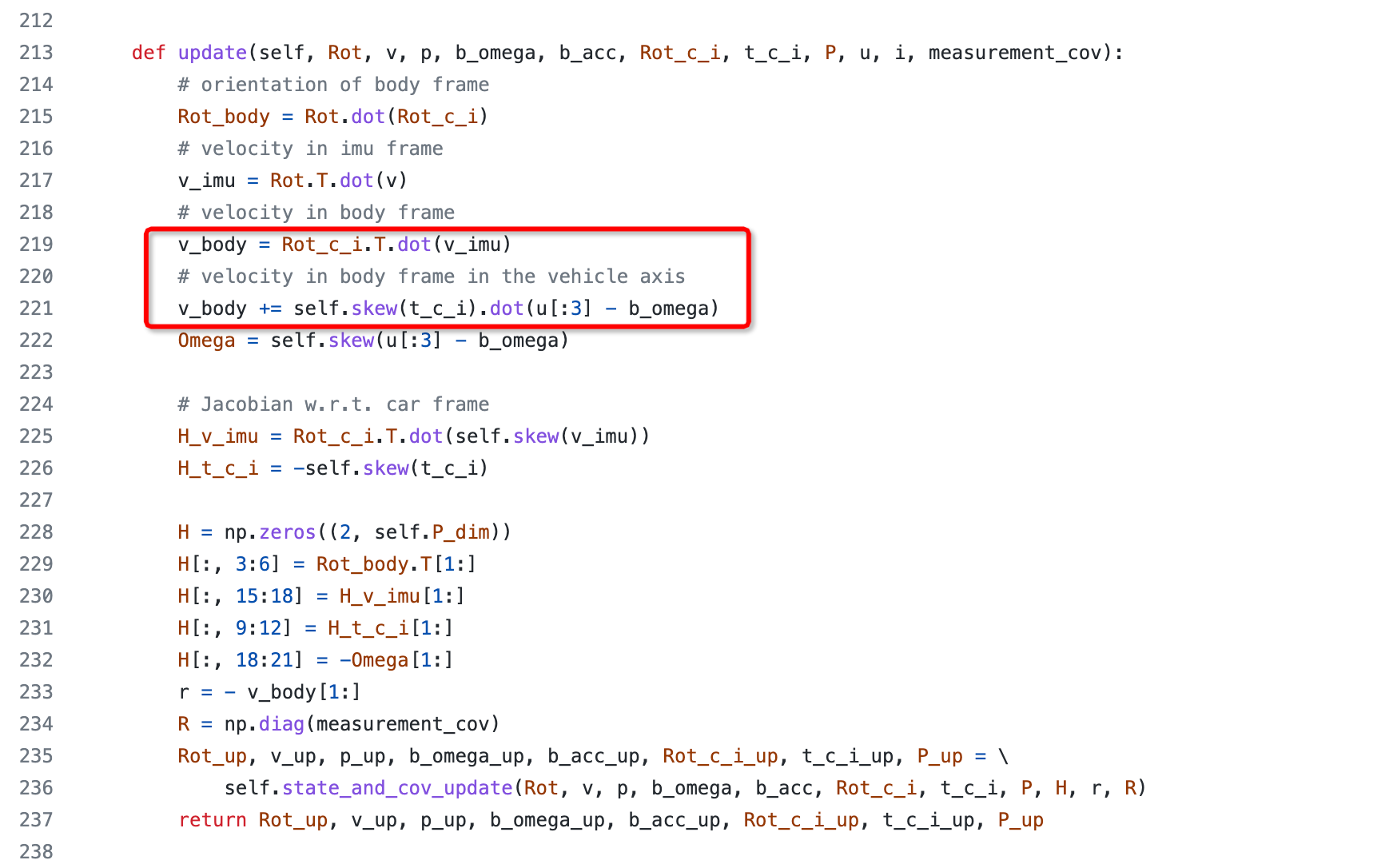 the formula in paper is
the formula in paper is