Extruding a 3D surface

[dt99jay]

Is there a correct way to extrude a 2.5/3D surface? At the moment I'm extruding a 2D surface, then editing the 'original' vertices (i.e. those left at z=0) with the shape of my surface:

import numpy as np
from scipy.spatial import Delaunay
import trimesh

# Generate coordinates
x = np.arange(0, 10)
y = np.arange(0, 10)
z = np.random.rand(10,10).round(2)
xx, yy = np.meshgrid(x, y)

# Triangulate
coords = np.vstack(np.dstack((xx, yy)))
tris = Delaunay(coords)

# Mesh
mesh = trimesh.creation.extrude_triangulation(
    vertices=coords, faces=tris.simplices, height=-10
)

# Edit non-extruded verts with correct z values
verts = mesh.vertices.view(np.ndarray)
verts[verts[:,2] == 0, 2] = z.reshape(-1)

mesh.export(file_obj="mesh.ply");

Thanks for Trimesh – it's very handy to have a pure python mesh library.

[HollowHeartNet]

Dear all,

I also would like to know how to achieve an extrusion for 3D surfaces. Please help. Here an example for a better explanation of my problem:

1.) Input mesh plane:

2.) Output using trimesh extrusion for 2D triangulation (ignoring z values):

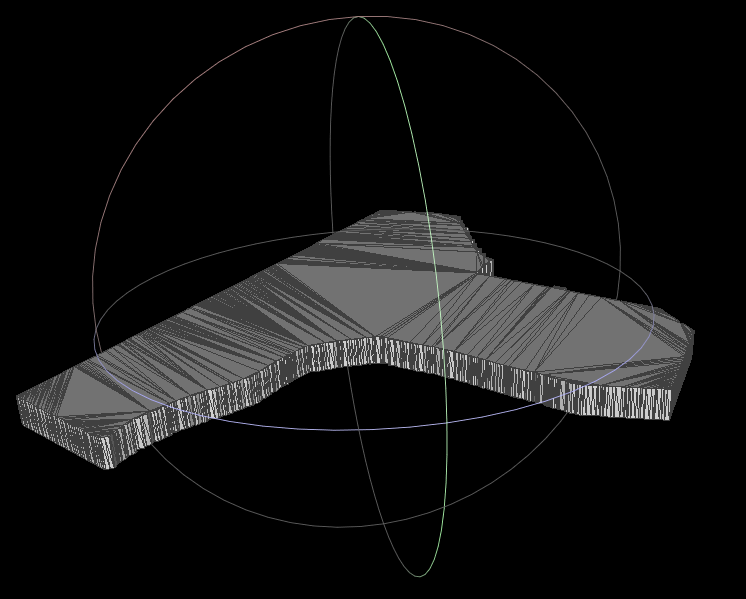
3.) Output using the proposed approach of @dt99jay for considering the z values:

4.) Expected result (I used the extrusion function in Blender for this case):

Do you know how I can get the same result such as in 4.) with trimesh or any other python library?

[manuel-koch]

I was playing with extrusion of a convex mesh into arbitrary direction and used a slight adaption of the existing functionality of trimesh.creation.extrude_triangulation:

Maybe this helps if you use the faces of you model at faces_to_extrude and pick a useful direction ?

def get_mesh_faces_in_direction(mesh, direction_normal, tol_dot=0.01):
    face_idxs = []
    for face_idx, face_normal in enumerate(mesh.face_normals):
        face_normal = face_normal / np.linalg.norm(face_normal)
        face_dir_dot = np.dot(face_normal, direction_normal)
        if face_dir_dot > tol_dot:  # face normal in same direction ?
            face_idxs.append(face_idx)
    return mesh.faces[face_idxs]

def extrude_convex_mesh(mesh, direction):
    assert mesh.is_convex, "Can only extrude convex meshes"

    normal = direction / np.linalg.norm(direction)

    faces_to_extrude = get_mesh_faces_in_direction(mesh, normal)

    # code slightly adapted from `trimesh.creation.extrude_triangulation`

    # stack the (n,3) faces into (3*n, 2) edges
    edges = trimesh.geometry.faces_to_edges(faces_to_extrude)
    edges_sorted = np.sort(edges, axis=1)
    # edges which only occur once are on the boundary of the polygon
    # since the triangulation may have subdivided the boundary of the
    # shapely polygon, we need to find it again
    edges_unique = trimesh.grouping.group_rows(
        edges_sorted, require_count=1)

    # (n, 3, 2) set of line segments (positions, not references)
    boundary = mesh.vertices[edges[edges_unique]]

    # we are creating two vertical triangles for every 3D line segment
    # on the boundary of the 3D triangulation
    vertical = np.tile(boundary.reshape((-1, 3)), 2).reshape((-1, 3))
    vertical[1::2] += direction
    vertical_faces = np.tile([3, 1, 2, 2, 1, 0],
                             (len(boundary), 1))
    vertical_faces += np.arange(len(boundary)).reshape((-1, 1)) * 4
    vertical_faces = vertical_faces.reshape((-1, 3))

    # reversed order of vertices, i.e. to flip face normals
    bottom_faces_seq = faces_to_extrude[:, ::-1]

    top_faces_seq = faces_to_extrude.copy()

    # a sequence of zero- indexed faces, which will then be appended
    # with offsets to create the final mesh
    faces_seq = [bottom_faces_seq,
                 top_faces_seq,
                 vertical_faces]
    vertices_seq = [mesh.vertices,
                    mesh.vertices.copy() + direction,
                    vertical]

    # append sequences into flat nicely indexed arrays
    vertices, faces = trimesh.util.append_faces(vertices_seq, faces_seq)

    # create mesh object
    extruded_mesh = trimesh.Trimesh(vertices=vertices, faces=faces)
    extruded_mesh.fix_normals() # somehow face normals are inverted for some `direction`, fixing it here
    return extruded_mesh

[manuel-koch]

E.g. for a cube / sphere the result might look like the following ( gray is the original mesh, red is the extruded mesh ):

[dylanjkline]

Hi @manuel-koch, can you provide a code on how you extruded the sphere? Also, can this be extended along a path? It seems that I am having a problem retaining a convex mesh using this method.

[manuel-koch]

Hi @dylanjkline, for my use-case I only needed to extrude along a straight line.

I tried it by creating a sphere using sphere = trimesh.creation.icosphere(subdivisions=3, radius=2)

The result of my extrude_convex_mesh() creates a convex mesh of the extruded part - i.e. the sphere is still there as-is ( drawn in gray in my screenshot ) and the extruded mesh is "clued" to it ( drawn in red ), but both meshes are not connected.

That may not exactly what you expect it to be - I guess you expect that the extruded part is replacing the "upper" part of the sphere in the example screenshot, which is actually not the case.