See the section "INFORMATION THEORETIC CRITERIA" for derivation.
How the author proved effectiveness of the proposal?
Tested the performance for two classic problems of system identification and prediction
Any discussions?
As stated in the paper, the following part might suggest the important point to think about adaptive step-size:
"However, we show that MEE performs better than MEE-SAS in situations where tracking ability of the optimal solution is required like in the case of non-stationary signals."
"A new normalized minimum-error entropy (NMEE) algorithm is proposed as an alternative to the minimum-error entropy (MEE) and the minimum-error entropy with self-adjusting step size (MEE-SAS) algorithms. The proposed NMEE algorithm requires fewer iterations and less computation to converge and yields lower misadjustment as compared to those of the MEE and the MEE-SAS algorithms."
Summary
Link
An Improved Minimum Error Entropy Criterion with Self Adjusting Step-Size
Author/Institution
Seungju Han, Sudhir Rao, D. Erdogmus, J. Principe University of Florida and Oregon Health and Science University
What is this
Comparison with previous researches. What are the novelties/good points?
Comparison with MEE
Key
MEE\mbox{-}SAS: J(e) = min_{\mathbf w}[V(0) - V(e)]^2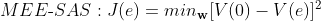
where $V(e)$ can be approximated by
$V(e) \approx \frac{1}{L} \sum{i=k-L}^{k-1}\mathbf{K}{\sigma\sqrt{2}}(e_k-e_i)$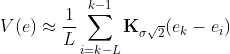
See the section "INFORMATION THEORETIC CRITERIA" for derivation.
How the author proved effectiveness of the proposal?
Tested the performance for two classic problems of system identification and prediction
Any discussions?
As stated in the paper, the following part might suggest the important point to think about adaptive step-size: "However, we show that MEE performs better than MEE-SAS in situations where tracking ability of the optimal solution is required like in the case of non-stationary signals."
What should I read next?