Thank you very much for providing this information @workingjubilee!
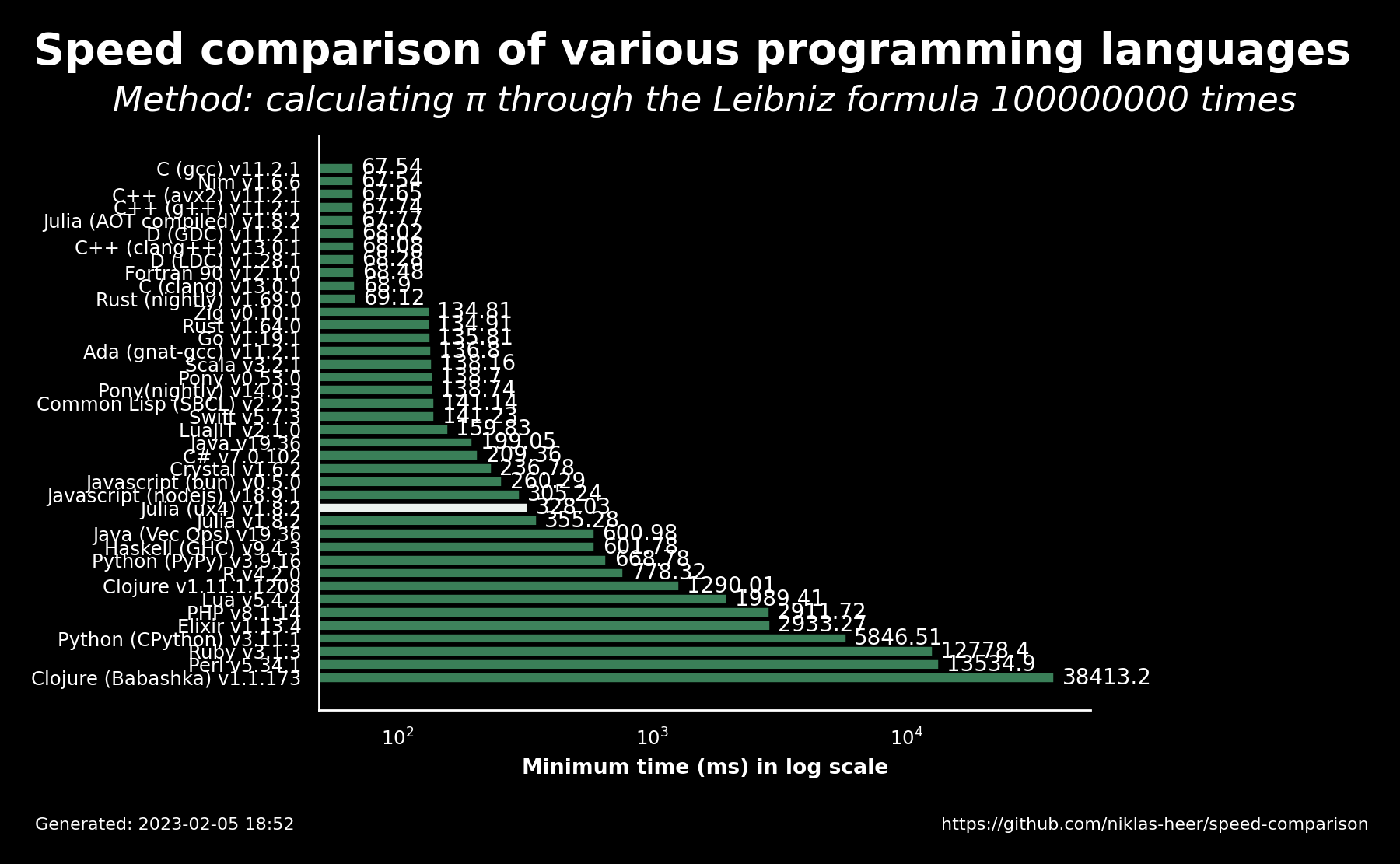
I try to display this information in the generated image. The lighter the green, the less accurate the result.
Closed workingjubilee closed 2 years ago
Thank you very much for providing this information @workingjubilee!
I try to display this information in the generated image. The lighter the green, the less accurate the result.

It's worth noting the languages produce wildly divergent results:
One might incorrectly assume they all should produce roughly the same result, but that would only hold if they all use the same floating point implementations. Some divergence might still be expected for those which do. But the C and C++ results are wildly different.
Part of that is due to currently using a float (or "binary32"), which is less accurate. However, even resizing the use of a double as in other languages can produce a different result, in my experiments, so I don't think that's the entire explanation. Part of that is due to numeric promotion implicit in the C language, I expect.
Another reason that might be why is that gcc's default compilation settings allow it to do various implicit """optimizations""" that are illegal under most language semantics, because they can make certain calculations more precise by reducing the number of roundoffs, but make other calculations fail by introducing inaccuracy instead (e.g. making
0.0 == (y * x + b) - (y * x + b)fail). One of them in gcc is toggled by-ffp-contract, and defaults to=fast.For that one, at least, it might be intentional to use something like that in this case, as certainly it seems to make the Leibniz computation go... faster, I guess. If so, then all the languages that have an
fmaorfmaffunction should probably be optionally using it. An FPU with "fused multiply-add", which most do nowadays, will actually perform multiplication as something roughly equivalent tofma(a, b, 0.0), with addition asfma(1.0, b, c), wherefma(a, b, c)isa * b + cbut in "one step" (a single rounding).