习题8-3

[zhengyangWang1]

当将自注意力模型作为一个神经层使用时，分析它和卷积层以及循环层在建模长距离依赖关系的效率和计算复杂度方面的差异.

[zhengyangWang1]

基于卷积或循环网络的序列编码都是一种局部的编码方式，只建模了输入信息的局部依赖关系．虽然循环网络理论上可以建立长距离依赖关系，但是由于信息传递的容量以及梯度消失问题，实际上也只能建立短距离依赖关系。 RNN梯度消失的原因是，随着梯度的传导，梯度被近距离梯度主导，模型难以学习到远距离的信息。具体原因也就是 $\prod_{k=t+1}^{T} \frac{\partial h^{(k)}}{\partial h^{(k-1)}}$ 部分，在迭代过程中，每一步 $\frac{\partial h^{(k)}}{\partial h^{(k-1)}}$ 始终在 $[0,1]$ 之间或者始终大于1。 因此，卷积层和循环层不适合用于建模长距离依赖关系。 如果要建立输入序列之间的长距离依赖关系，可以使用以下两种方法：

1. 增加网络的层数，通过一个深层网络来获取远距离的信息交互
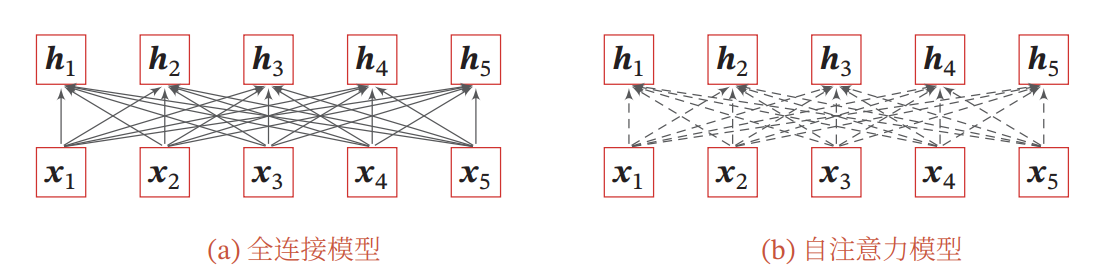
2. 使用全连接网络。 而全连接网络无法处理变长序列，自注意力模型可以解决这个问题，因为其连接权重是动态学习的。

复杂度：

循环层： $h{t}=f\left(U x{t}+W h_{t-1}\right)$

• $U x_{t}: d \times m 与 m \times 1$ 运算，复杂度为 $\mathcal{O}(m d)$ ， m为input size
• $W h_{t-1}: d \times d 与 d \times 1$ 运算，复杂度为 $\mathcal{O}\left(d^{2}\right)$

故一次操作的时间复杂度为 $\mathcal{O}\left(d^{2}\right)$ ， n次序列操作后的总时间复杂度为 $\mathcal{O}\left(n d^{2}\right)$

卷积层： 注: 这里保证输入输出都是一样的，即均是 $n \times d$

• 为了保证输入和输出在第一个维度都相同，故需要对输入进行padding操作，因为这里kernel size为k， (实际kernel的形状为 $k \times d$ ) 如果不 padding的话，那么输出的第一个维度为 $n-k+1$ ，因为这里stride是为1的。为了保证输入输出相同，则需要对序列的前后分别padding长度为 $(k-1) / 2$ 。
• 大小为 $k \times d$ 的卷积核一次运算的复杂度为: $\mathcal{O}(k d)$ ，一共做了 n 次，故复杂度为 $\mathcal{O}(n k d)$
• 为了保证第二个维度在第二个维度都相同，故需要 d 个卷积核，所以卷积操作总的时间复杂度为 $\mathcal{O}\left(n k d^{2}\right)$

自注意力层： $A(Q, K, V)={Softmax}\left(Q K^{T}\right)$

• $Q, K, V: n \times d$
• 相似度计算 $Q K^{T}: n \times d 与 d \times n$ 运算，得到 $n \times n$ 矩阵，复杂度为 $\mathcal{O}\left(n^{2} d\right)$
• softmax计算: 对每行做softmax，复杂度为 $\mathcal{O}(n)$ ,则 $\mathrm{n}$ 行的复杂度为 $\mathcal{O}\left(n^{2}\right)$
• 加权和: $n \times n$ 与 $n \times d$ 运算，得到 $n \times d$ 矩阵，复杂度为 $\mathcal{O}\left(n^{2} d\right)$ .故最后self-attention的时间复杂度为 $\mathcal{O}\left(n^{2} d\right)$

参考文献： LSTM如何解决RNN带来的梯度消失问题 - 知乎 Transformer/CNN/RNN的对比（时间复杂度，序列操作数，最大路径长度） - 知乎