double value call toStyledString show Loss of precision

[HeYang6]

Why is 71.20999999999999 displayed when it is clearly 71.21

[BillyDonahue]

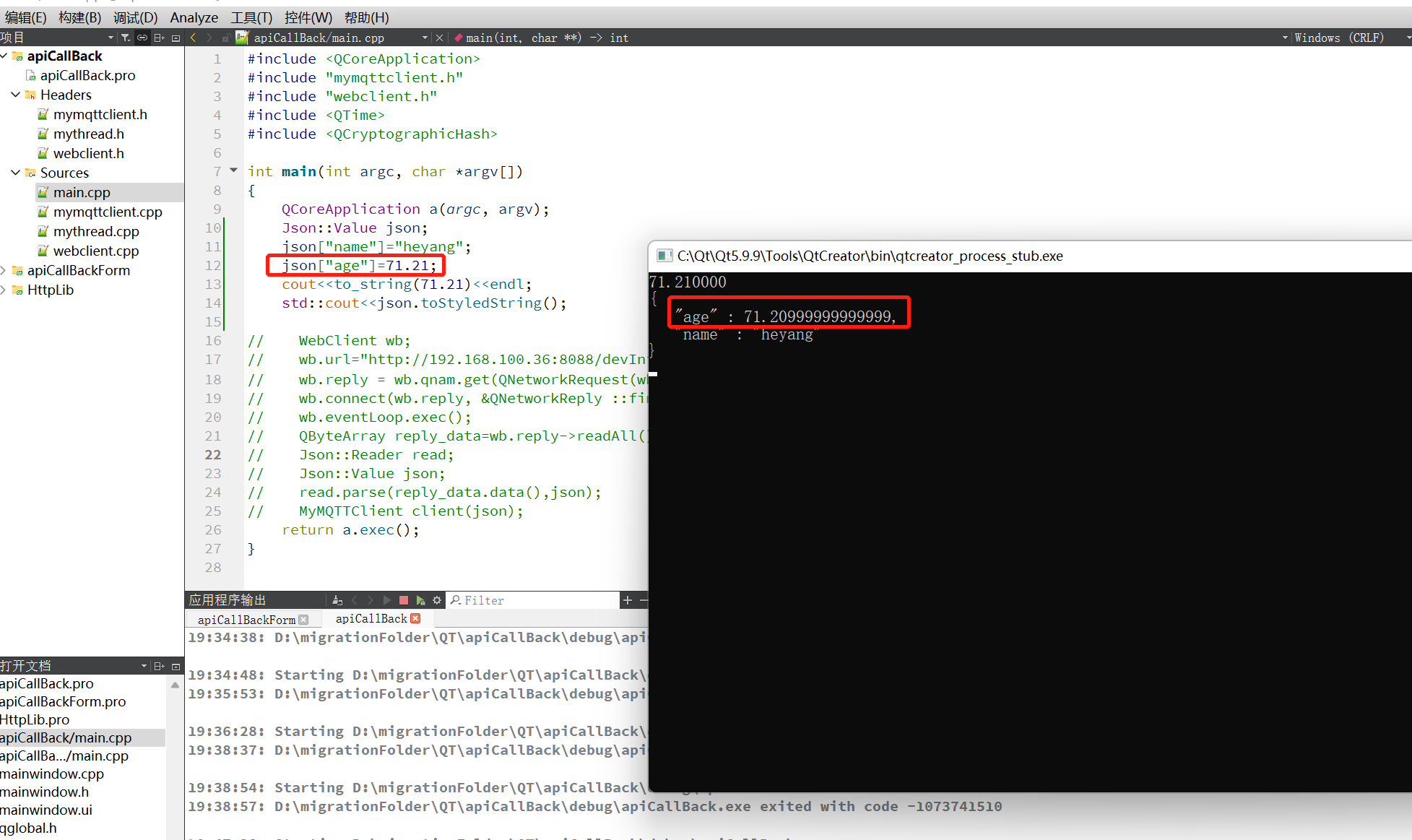
Because 21/100 doesn't have an exact floating point representation and you haven't said how much precision you want to keep in your json.toStyledString() call..

This is due to subtlety in the meaning of the decimal numeric limits of the double data type.

We're using 17 digits by default, because this is how many digits are needed in order to unambiguously represent any value of double as a string. This 17 == DBL_DECIMAL_DIG == std::numeric_limits<double>::max_digits10. Printing with this precision guarantees that any double value can be survive being printed and parsed again without distortion.

This is different from the 15 == DBL_DIG == std::numeric_limits<double>::digits10, which is the max number of digits that can be parsed from string to double and back without being distorted.

So the default of 17 is a tradeoff. We chose enough digits to represent every possible double precision value perfectly. That's not what you are trying to do, though. You want only 15 digits of precision, because 15 digits can be parsed and reprinted without distortion, but it sacrifices access to the full mantissa of the double data type.

There's a way to set precision if you need to customize the output and use a custom configured writer.

https://github.com/open-source-parsers/jsoncpp/blob/8190e061bc2d95da37479a638aa2c9e483e58ec6/src/lib_json/json_writer.cpp#L1240

I hope that helps.

[BillyDonahue]

Here's a demonstration of these precision effects. At 15 digits, your 71.21 number is represented as you expected.

By printing beyond 15 digits, we can start to see that the stored floating point bit pattern could never be said to be 71.21 exactly. It's representing a number somewhere in this narrow range:

(71.2099999999999937472239...,
 71.2100000000000079580786...]
                 ^
 00 0000000111111  (digit indexes)
 12 3456789012345

If you only print 15 digits you'll see numbers that are exactly preserved from the values they were parsed from. But the drawback is that if the parsed number was specified using more than 15 digits, information would be lost by parsing and printing it.

#include <iostream>
#include <iomanip>
#include <string>
#include <cmath>

constexpr double inf = std::numeric_limits<double>::infinity();

void dumpTable(double x) {
    int maxPrecision = 25;
    double xPlusEpsilon = std::nextafter(x, inf);
    for (int p = 0; p < maxPrecision; ++p) {
        std::cout << "p=" << std::setw(3) << p;
        for (auto f : {x, xPlusEpsilon}) {
            std::cout
                << ", "
                << std::setprecision(p)
                << std::defaultfloat
                << std::setw(maxPrecision + 5)
                << f;
        }
        std::cout << std::endl;
    }
}

int main() {
    dumpTable(71.21);
    return 0;
}

p=  0,                          7e+01,                          7e+01
p=  1,                          7e+01,                          7e+01
p=  2,                             71,                             71
p=  3,                           71.2,                           71.2
p=  4,                          71.21,                          71.21
p=  5,                          71.21,                          71.21
p=  6,                          71.21,                          71.21
p=  7,                          71.21,                          71.21
p=  8,                          71.21,                          71.21
p=  9,                          71.21,                          71.21
p= 10,                          71.21,                          71.21
p= 11,                          71.21,                          71.21
p= 12,                          71.21,                          71.21
p= 13,                          71.21,                          71.21
p= 14,                          71.21,                          71.21
p= 15,                          71.21,                          71.21
p= 16,              71.20999999999999,              71.21000000000001
p= 17,             71.209999999999994,             71.210000000000008
p= 18,            71.2099999999999937,             71.210000000000008
p= 19,           71.20999999999999375,           71.21000000000000796
p= 20,          71.209999999999993747,          71.210000000000007958
p= 21,         71.2099999999999937472,         71.2100000000000079581
p= 22,        71.20999999999999374722,        71.21000000000000795808
p= 23,       71.209999999999993747224,       71.210000000000007958079
p= 24,      71.2099999999999937472239,      71.2100000000000079580786

[HeYang6]

OK,thank you very much