A low signal to noise ration (high CVrmse) can be caused by randomness in the signal at times that are not particularly relevant to the retrofit. For example, what if the expected savings are all happening during the occupied hours (weekday). Any noise on the weekends could be ignored. Applying a strategy of removing noise this way would require a good ex-ante load shape model. And that's probably a good topic for another issue.




 We have reason to believe this home used over 1200 kWh for heating over the past 12 months. But because the intercept_only model was assigned, this portion of electric use will not be weather-normalized in CalTRACK. This could result in significant errors when calculating savings... depending entirely on the specific weather changes between baseline and reporting periods: savings could be under- or over-reported. Over a large pool of homes this might wash out, as Hassan pointed out during the call.
We have reason to believe this home used over 1200 kWh for heating over the past 12 months. But because the intercept_only model was assigned, this portion of electric use will not be weather-normalized in CalTRACK. This could result in significant errors when calculating savings... depending entirely on the specific weather changes between baseline and reporting periods: savings could be under- or over-reported. Over a large pool of homes this might wash out, as Hassan pointed out during the call.
 Figure 1. Comparison of different model-fit metrics for intercept-only models in commercial buildings.
Figure 1. Comparison of different model-fit metrics for intercept-only models in commercial buildings. Figure 2. Energy use vs. model fit characteristic diagram. Building types in region A are potential candidates for CalTRACK modeling, region B may require submetering and region C require additional independent variables.
Figure 2. Energy use vs. model fit characteristic diagram. Building types in region A are potential candidates for CalTRACK modeling, region B may require submetering and region C require additional independent variables.
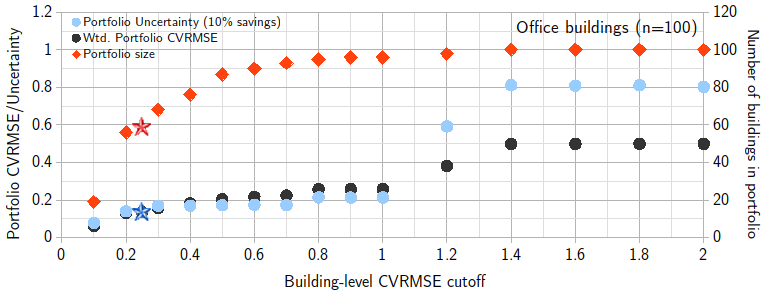
 Figure 3. Variation of portfolio size, weighted mean CVRMSE and portfolio fractional savings uncertainty with different building-level CVRMSE cutoffs for office buildings. Stars represent the ASHRAE Guideline 14 recommended cutoff (CVRMSE=25%).
Figure 3. Variation of portfolio size, weighted mean CVRMSE and portfolio fractional savings uncertainty with different building-level CVRMSE cutoffs for office buildings. Stars represent the ASHRAE Guideline 14 recommended cutoff (CVRMSE=25%).
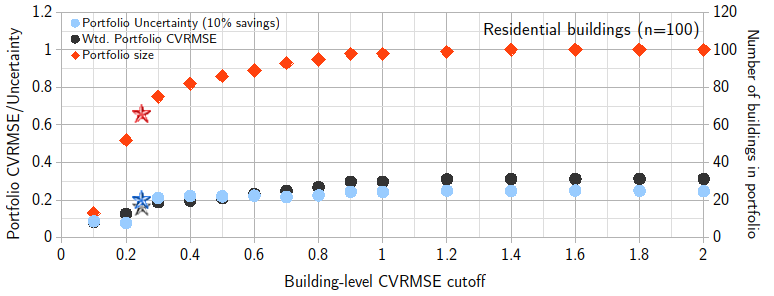
 Figure 4. Variation of portfolio size, weighted mean CVRMSE and portfolio fractional savings uncertainty with different building-level CVRMSE cutoffs for residential buildings. Stars represent the ASHRAE Guideline 14 recommended cutoff (CVRMSE=25%).
Figure 4. Variation of portfolio size, weighted mean CVRMSE and portfolio fractional savings uncertainty with different building-level CVRMSE cutoffs for residential buildings. Stars represent the ASHRAE Guideline 14 recommended cutoff (CVRMSE=25%).
Buildings with usage patterns that are not correctly captured using Caltrack models end up with low signal-to-noise ratio, poor model fits and tend to default to the intercept-only model. These buildings are not suitable for Caltrack/regression modeling and are recommended to be handled using alternate methods.
We propose the following: