NURBS.surfaces: derivatives evaluation

Describe the bug I did a NURBS approximation of a 3D model in Rhino resulting in several NURBS surfaces. I calculated the derivatives for one of the resulting surfaces and figured out some strange effects. The following image shows the surface at the top left. The other 3 plots shows the x-, y- and z-part of the derivative of the surface with respect to u. In each part of the derivative there are some jumps across the surface which are obviosly wrong.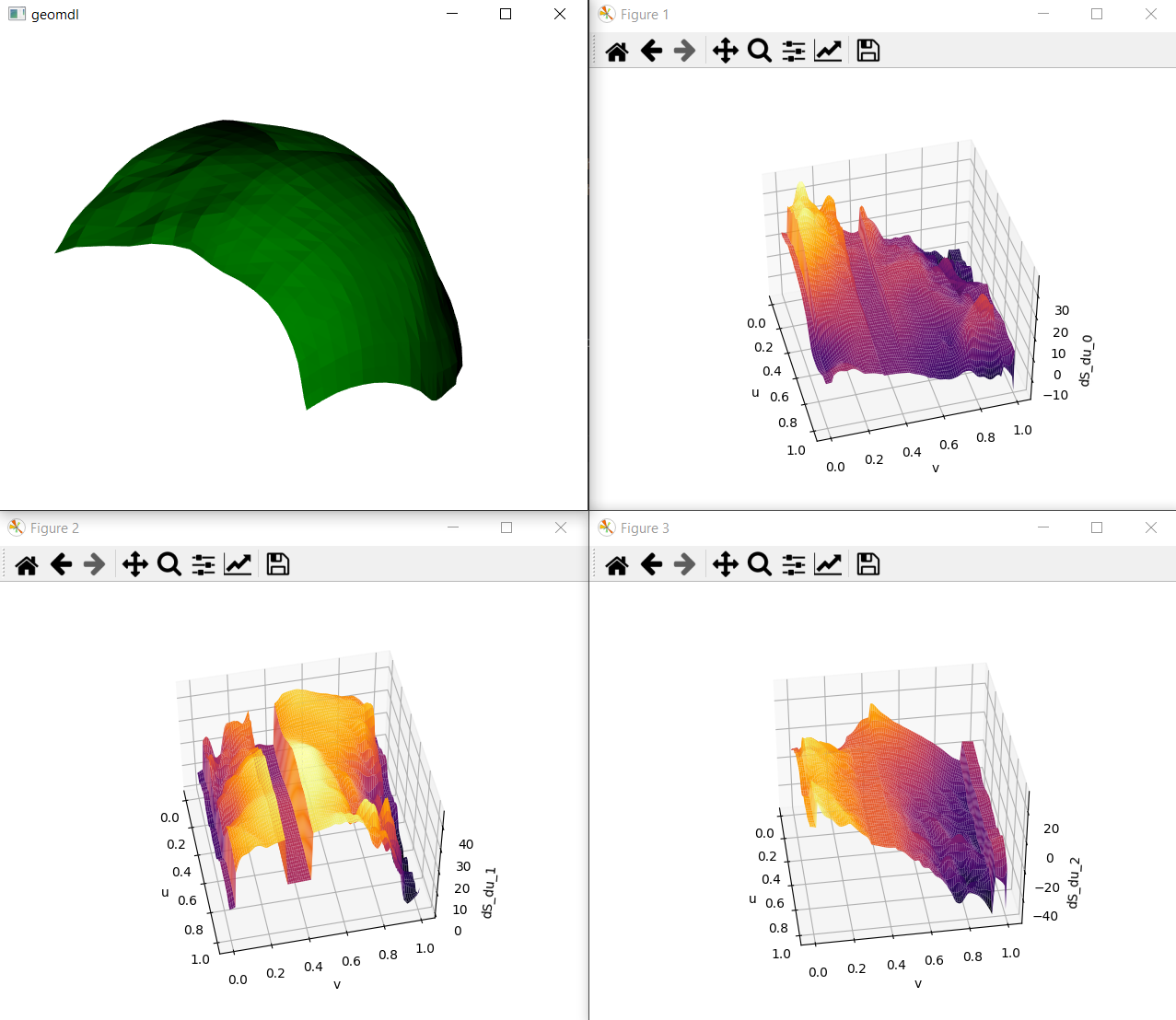 python_figures

I made the same plots in Matlab using the NURBS Toolbox: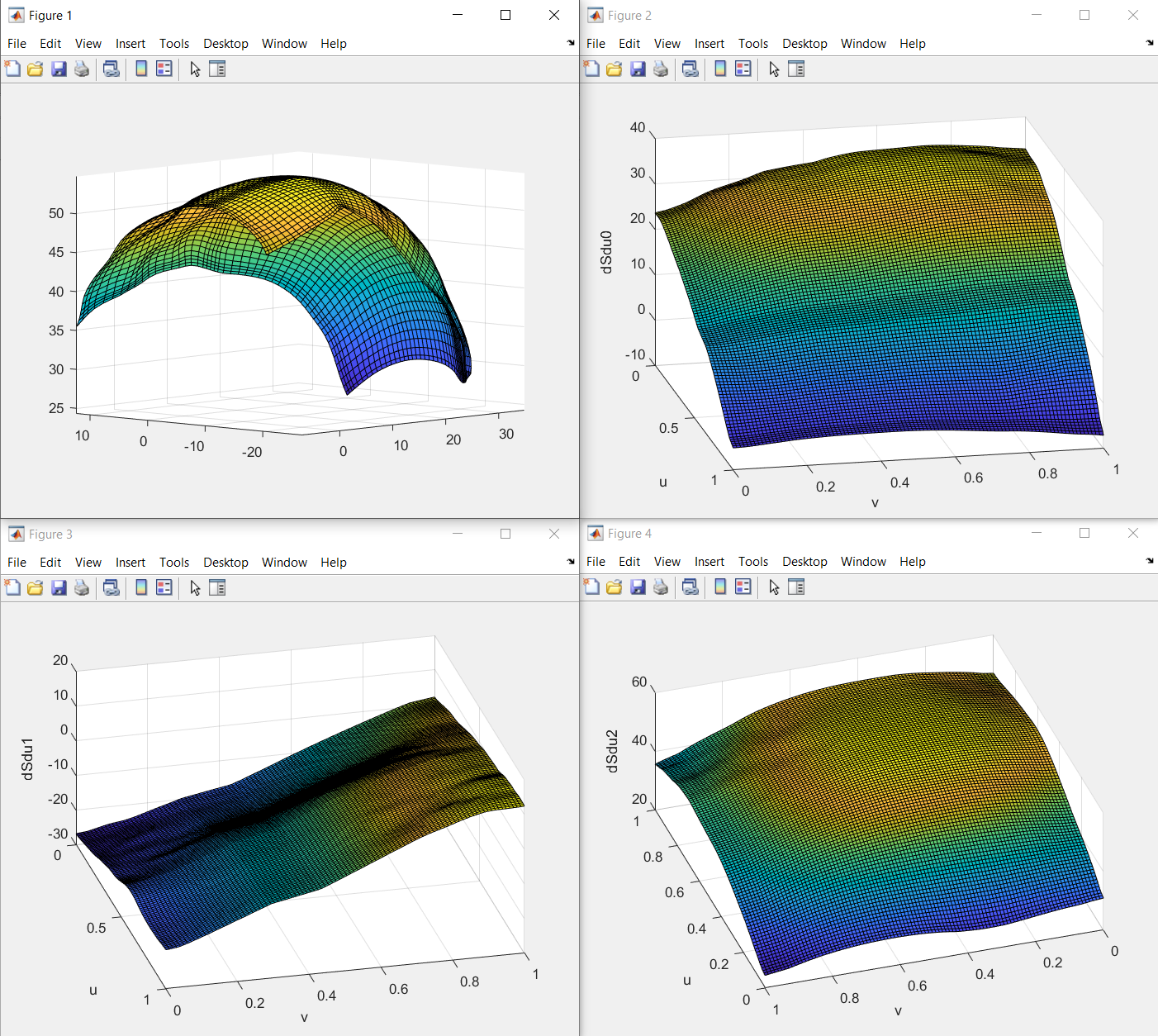 matlab_figures

To Reproduce Steps to reproduce the behavior: I exported the surface knots vectors and ctrlpts into export.mat in the zip file. nurbs_surface.zip

Python code:

from geomdl import NURBS
from geomdl.visualization import VisVTK
import matplotlib.pyplot as plt
import scipy.io
import numpy as np

if __name__ == '__main__':
    data = scipy.io.loadmat('export.mat')
    knotvector_u = data['knotvector_u'].tolist()[0]
    knotvector_v = data['knotvector_v'].tolist()[0]
    ctrlpts = data['ctrlpts'].tolist()
    ctrlpts = [ctprlt for sublist in ctrlpts for ctprlt in sublist]
    surf = NURBS.Surface()
    # Set degrees
    surf.degree_u = 3
    surf.degree_v = 3

    # Set control points (weights vector will be 1 by default)
    surf.set_ctrlpts(ctrlpts, 73, 95)

    # Set knot vectors
    surf.knotvector_u = knotvector_u
    surf.knotvector_v = knotvector_v

    surf.vis = VisVTK.VisSurface(ctrlpts=False, legend=False)
    surf.render()

    grid_size = 100
    u = np.linspace(0, 1, grid_size)
    v = np.linspace(0, 1, grid_size)
    U, V = np.meshgrid(u, v)
    dS_du = np.zeros((u.shape[0], v.shape[0], 3))
    #dS_dv = np.zeros((u.shape[0], v.shape[0], 3))

    for i in range(u.shape[0]):
        for j in range(v.shape[0]):
            SKL = surf.derivatives(u[i], v[j], 1)
            dS_du[i, j, :] = SKL[1][0]
            #dS_dv[i, j, :] = SKL[0][1]

    idx = 0
    fig = plt.figure()
    ax = plt.axes(projection='3d')
    ax.plot_surface(U, V, dS_du[:, :, idx], rcount=grid_size, cmap='inferno')
    ax.set_xlabel('u')
    ax.set_ylabel('v')
    ax.set_zlabel('dS_du_' + str(idx))
    plt.show(block=False)

    idx = 1
    fig = plt.figure()
    ax = plt.axes(projection='3d')
    ax.plot_surface(U, V, dS_du[:, :, idx], rcount=grid_size, cmap='inferno')
    ax.set_xlabel('u')
    ax.set_ylabel('v')
    ax.set_zlabel('dS_du_' + str(idx))
    plt.show(block=False)

    idx = 2
    fig = plt.figure()
    ax = plt.axes(projection='3d')
    ax.plot_surface(U, V, dS_du[:, :, idx], rcount=grid_size, cmap='inferno')
    ax.set_xlabel('u')
    ax.set_ylabel('v')
    ax.set_zlabel('dS_du_' + str(idx))
    plt.show()

    print('Done.')

Matlab code:

clear;
close all;
clc;

addpath("nurbs_toolbox"); % https://de.mathworks.com/matlabcentral/fileexchange/26390-nurbs-toolbox-by-d-m-spink
load("export.mat");

ctrlpts = permute(ctrlpts, [3,1,2]);
srf   = nrbmak(ctrlpts,{knotvector_u knotvector_v});
dsrf = nrbderiv(srf);

u = linspace(0, 1);
v = linspace(0, 1);

[UU, VV] = meshgrid(u, v);

deriv = nrbdeval(srf, dsrf, {u,v});

nrbplot(srf, [50 50]);

figure();
surf(UU, VV, reshape(deriv(1,:,:), numel(u), numel(v)));
xlabel('u'); ylabel('v'), zlabel('dSdu0');
figure();
surf(UU, VV, reshape(deriv(2,:,:), numel(u), numel(v)));
xlabel('u'); ylabel('v'), zlabel('dSdu1');
figure();
surf(UU, VV, reshape(deriv(3,:,:), numel(u), numel(v)));
xlabel('u'); ylabel('v'), zlabel('dSdu2');

Configuration:

OS: Windows 10
Python distribution: Anaconda
Python version: 3.9
geomdl install source: PyPI
geomdl version/branch: 5.3.1

orbingol / NURBS-Python

NURBS.surfaces: derivatives evaluation #157