Hi @xiaodaxia-2008,
this is desired behaviour: Ruckig will first and foremost try to get the kinematic state within the allowed limits as fast as possible. Only then a time-optimal trajectory is calculated.
In your example, if the velocity wouldn't get negative in the top right figure, the trajectory would stay slightly longer above the velocity limit. If the velocity would decrease to +1 directly, a positive jerk would be necessary while the velocity would still be above its limits. I hope that clears up this issue.
However, we can think about a setting that disables the braking trajectory. I'm not sure how hard this would be to implement.

If the contraints are changed online, then the trajectory is not optimal as it should be. The following image shows the whole trajectory, at t = 2, max_velocity is reduces from 3 to 1, then the velocity goes to negative unexpectedly.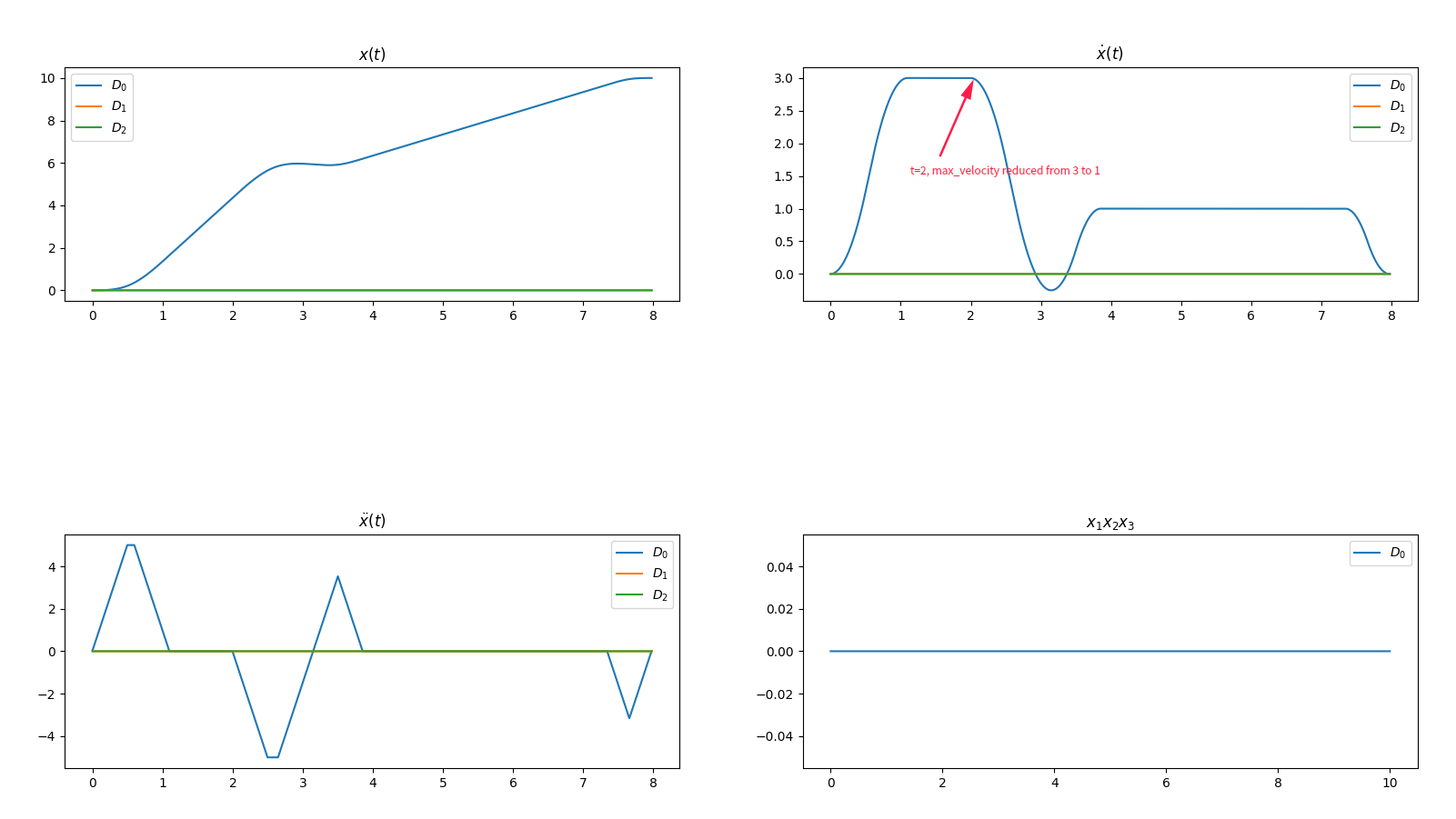
On the other hand, if the velocity constraints increases, everything seems to be fine.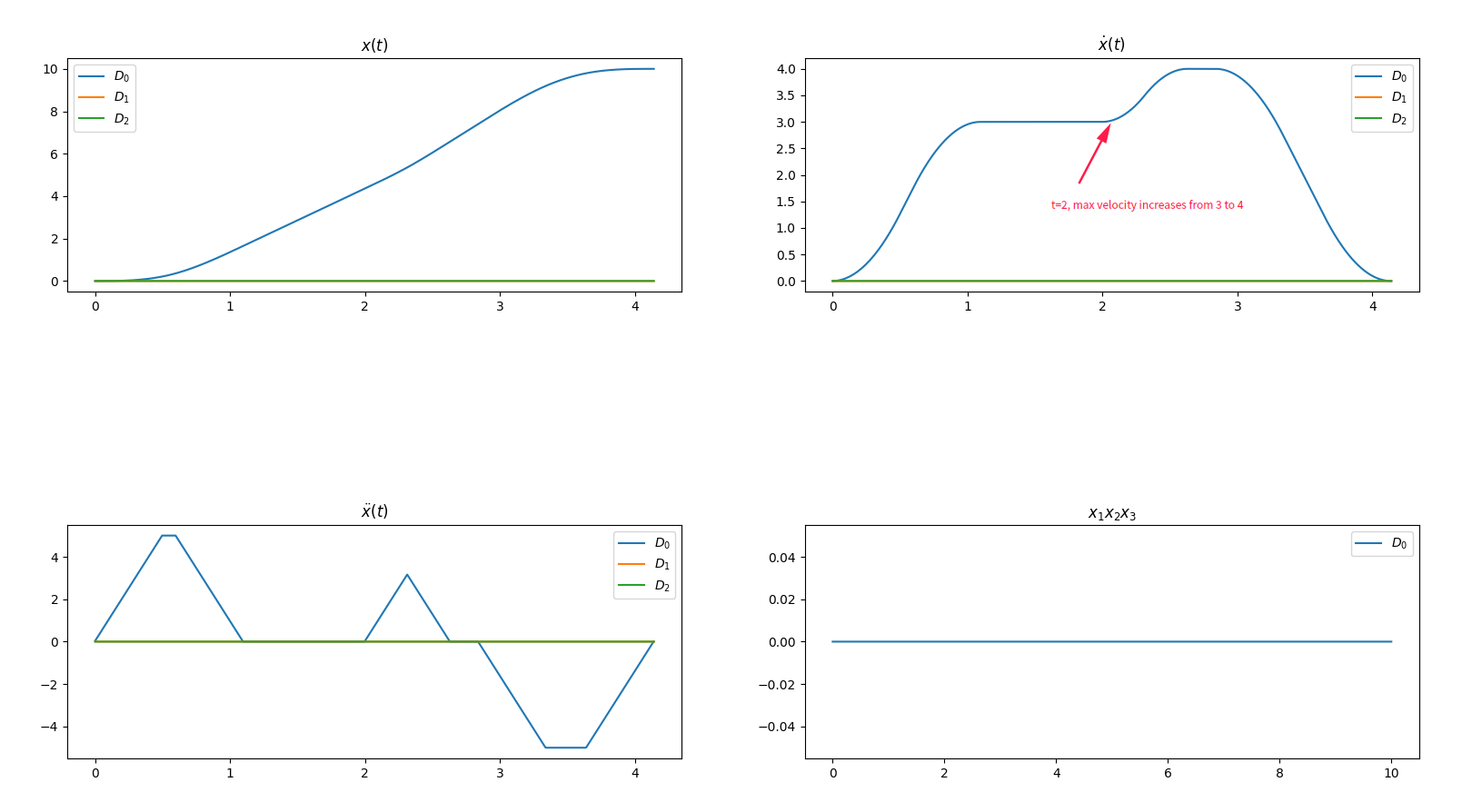
You could reproduce with the following code: