Sparse matrices / linear operators for differential equations

[pnkraemer]

We've known about this for a while now, I think it's time to at least make it an official feature-request. A solution is not urgent, though.

Matrices which are used in ODEPrior are, more often than not, of the form np.kron(mat1, mat2) usually even np.kron(np.eye(dim), mat). This allocation eats too much storage and has a slow MVM.

I propose to use a data structure such as for instance BlockDiagonal which only stores mat and dim and implements fast matrix-vector products:

class BlockDiagonal(pn.linalg.linops.LinearOperator):
    """
    Cheap implementation of np.kron(np.eye(num_copies), block).
    Optimised for a fast '@' operation.
    """

    __slots__ = ['block', 'num_copies']

    def __init__(self, block, num_copies):
        self.block = block
        self.num_copies = num_copies

    def toarray(self):
        return np.kron(np.eye(self.num_copies), self.block)

    def __add__(self, other):
        assert self.num_copies == other.num_copies
        return BlockDiagonal(self.block + other.block, self.num_copies)

    def __sub__(self, other):
        assert self.num_copies == other.num_copies
        return BlockDiagonal(self.block - other.block, self.num_copies)

    def __matmul__(self, other):
        if isinstance(other, BlockDiagonal):  # matmul
            assert self.num_copies == other.num_copies
            return BlockDiagonal(self.block @ other.block, self.num_copies)
        if isinstance(other, np.ndarray):  # matvec
            return (self.block @ other.reshape((self.block.shape[1], -1))).T.flatten()
        raise NotImplementedError

    @property
    def T(self):
        return BlockDiagonal(self.block.T, self.num_copies)

For projection matrices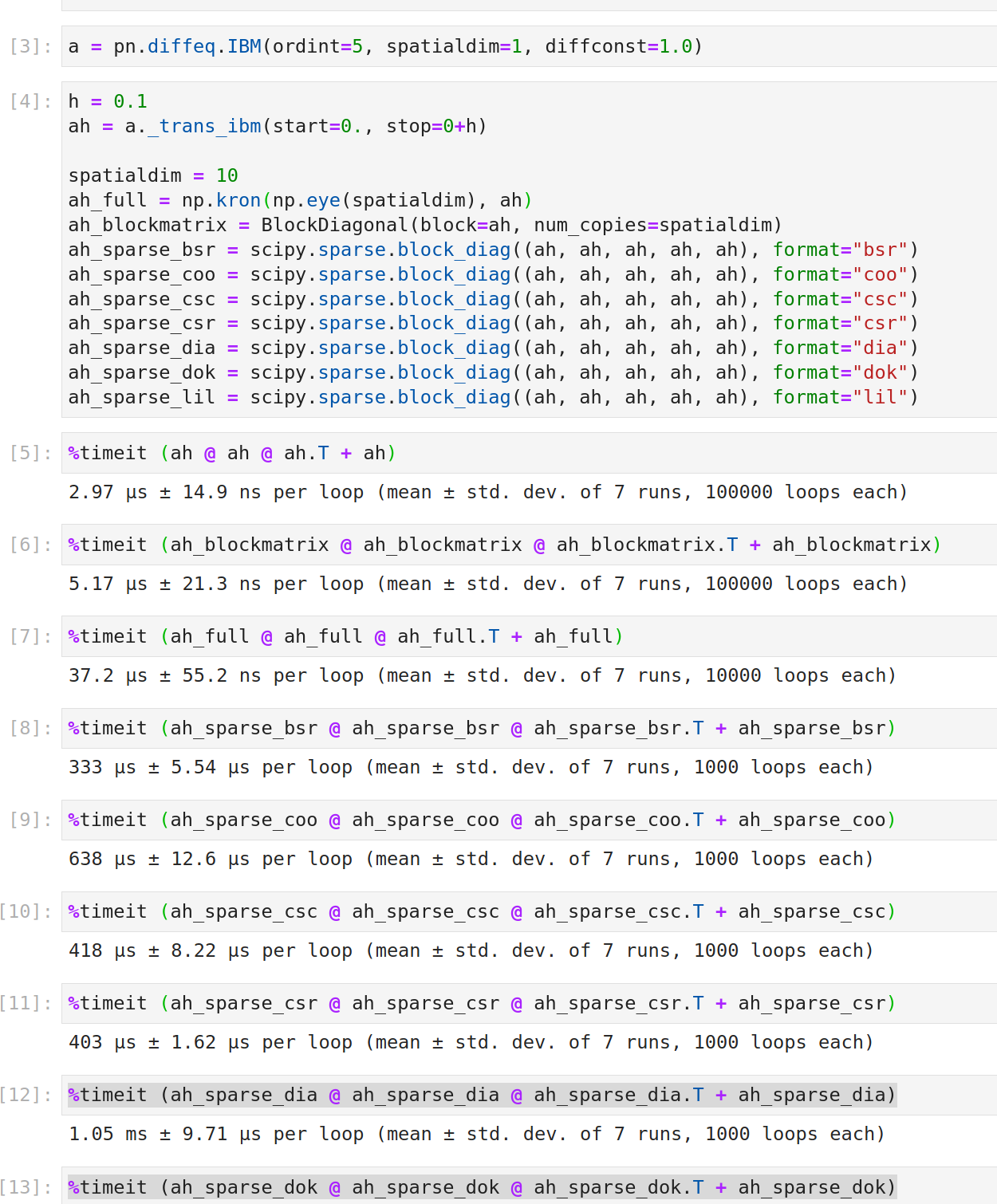 odeprior.proj2coord(), one could even go one step further and implement slicing into matmul (which I have not drafted yet). It would make the code equally readable (in my opinion; it would still use proj @ cov @ proj.T), the step to a more general kronecker product np.kron(mat1, mat2) would remain a simple extension (using e.g. (A \otimes B)(C \otimes D)=(A \otimes C)(B \otimes D); almost all involved matrices have this kronecker structure)) and the memory footprint as well as the speed would improve significantly (see below)

Affected files would be prior.py and ivp2filter.py which would need to replace the respective outputs by the data structure. Occasionally, np.linalg.solve() and np.linalg.cholesky() calls in ivpfiltsmooth.py and gaussfiltsmooth.py would have to be replaced. It could be a smart choice to subclass from linops.LinearOperator for interface reasons.

[JonathanWenger]

Having BlockDiagonal as a LinearOperator seems very convenient but is there a difference in efficiency or is this just an alias for the implemented Kronecker(A=Identity(num_copies), B=block)?

[pnkraemer]

Great, I wasn't aware that this already exists! Unfortunately there is a speed difference:

That doesn't mean that it is not a good idea to squeeze this data structure into linops, though. Perhaps we would like to pull linops up to random-variable-similar level, who knows...

[JonathanWenger]

It's very surprising that it is actually slower than the dense form of NumPy. That looks like a bug in the Kronecker implementation to me.

[pnkraemer]

Could be. Maybe it is because Kronecker doesn't implement matmul itself, so there is some nasty loopy thing going on somewhere else. I can't really judge.

[JonathanWenger]

Could be. Maybe it is because Kronecker doesn't implement matmul itself, so there is some nasty loopy thing going on somewhere else. I can't really judge.

That's a good guess. Matrix-vector multiplication is definitely much faster, since we use it in @ralfrost's thesis for efficient sampling from matrix-variate distributions.

Edit: This is now tracked in #210.

[nathanaelbosch]

I also think it would be a cool addition to probnum. I also think that these kinds of optimizations are not too critical, since the usage of such a block-matrix (or Kronecker matrix) would be just like a np.array, so it should be fairly easy to "switch back" to dense matrices if we would say at some point that it's too tedious to maintain our own special matrix types.

I have another benchmark request though! In PREDICT for example we compute $A P A^T + Q$. A and Q are of such a block-matrix type, but P is not. How does that compare? Can we even assume that we can make such an operation faster with this class of approaches (wrapping numpy functionality in custom Python classes)?

[pnkraemer]

I have another benchmark request though! In PREDICT for example we compute $A P A^T + Q$. A and Q are of such a block-matrix type, but P is not. How does that compare? Can we even assume that we can make such an operation faster with this class of approaches (wrapping numpy functionality in custom Python classes)?

Good question. It is faster, but only marginally (One might even say that they are "only" equally fast): I suppose that even if it is only "as" fast, the reduced storage may make this useful anyways. For e.g. EKF0, though, as long as the prior is of this form, the covariances are of this form (I think I am able to show this) in which case I expect the speedup to be significant. For EKF1 this will not always be the case as it depends on the form of the jacobian. .