VonMises distribution behaves poorly at the boundary

[alexlyttle]

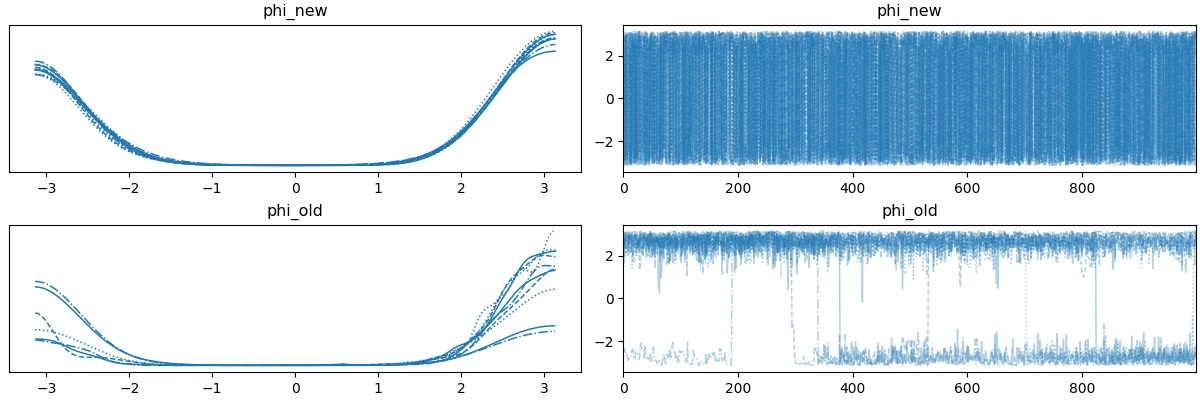
While converting my current work to numpyro, I noticed that the VonMises distribution doesn't sample well, especially when μ (or loc) is near ±π. I believe this is because the support for the VonMises distribution is the interval constraint from -π to +π. This does not allow the sampler to step from -π to +π or +π to -π by going over the boundary. I show the problem and a solution in my Gist here with plots below.

I would love to submit a PR with this fix if you agree that it improves/fixes the current VonMises distribution?

Solution

Click to expand

See [here](https://gist.github.com/alexlyttle/9510e10e0951fec356b9fc5bdd205f27) for code. My solution is to register a circular constraint as the `support` for the `VonMises` distribution by using a `CircularTransform` to allow the sampler to go over the boundary. The circular transform looks like this: 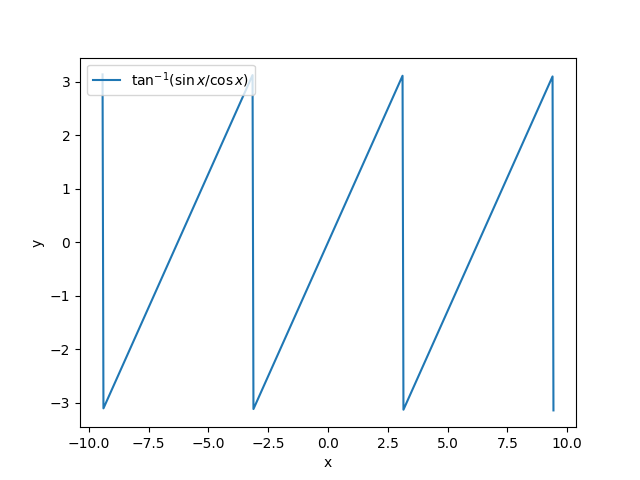 In the following plot, I show the trace for two variables sampled across 10 chains using the `numpyro` `NUTS` sampler: `phi_old` for the current VonMises distribution, and `phi_new` for my suggested fix. 

[fritzo]

Hi @alexlyttle your solution makes sense to me! I think we'll want to add that as a reparametrizer and register the new circular constraint and transform with transform_to() but not biject_to(), and I think we'll want to add a new improper distribution called say Sinusoidal or ImproperSinusoidal or something.

Note similar existing solution is to replace VonMises with ProjectedNormal distribution and reparametrize the model with ProjectedNormalReparam. That solution is similar in that it introduces a new auxiliary latent variable that is in many-to-one correspondence with the user-facing latent variable. If we follow that pattern also for circular then the CircularTransform would have .bijective = False, no defined .log_abs_det_jacobian(), but forward and backward that are pseudoinverses (like many other transforms). I think we could basically follow the ProjectedNormal software pattern everywhere (but with math replace by @alexlyttle's transforms).

[alexlyttle]

That's great :) I'm not so confident with the reparam module and it's usage, but I am keen to learn! I started a branch on my fork of numpyro earlier to implement my first suggestion but haven't submitted a PR yet as it may need more discussion re. what you have suggested. I'll try and wrap my head round this more tomorrow too, as the working day has just finished for me now.

[fritzo]

Sounds good @alexlyttle, let us know if you have any questions. Here's a rough guide of how I think your idea could most cleanly be added:

1. add a Circle or Circular constraint (following say constraints.sphere)

2. add a CircularReparam (following say ProjectedNormalReparam) something like this

   ```py class CirclularReparam(Reparam): def __call__(self, name, fn, obs): original_fn = fn fn, expand_shape, event_dim = self._unwrap(fn) # Draw parameter-free noise. new_fn = dist.Normal(0, 1).mask(False) # arbitrary, improper uniform value = numpyro.sample( f"{name}_unwrapped", self._wrap(new_fn, expand_shape, event_dim), obs=obs, ) # Differentiably transform. value = jnp.fmod(value, 2 * math.pi) # in [0, 2 * pi) # or maybe this? # value = jnp.fmod(value + math.pi, 2 * math.pi) - math.pi # in [-pi, pi) # Simulate a pyro.deterministic() site. numpyro.factor(f"{name}_factor", original_fn.log_prob(value)) return None, value ```

   I think that way you won't even need to use the atan2 pseudoinverse 🙂

3. add a unit test similar to other reparametrizer tests

(@fehiepsi in Pyro we could replace the above factor statement with a Delta(value, log_density=original_fn.log_prob(value)). Is there a particular reason NumPyro specially handles those as deterministic rather than coding them as Delta distributions? I'm not sure which pattern is cleaner, Delta as in Pyro or factor + deterministic as in the above NumPyro sketch)

[fehiepsi]

@fritzo It is just for convenience to record those values at deterministic sites in MCMC result (without having to use Predictive). We don't record the values at observed (Delta) sites.

[alexlyttle]

@fritzo Thanks for the suggestion. I tried implementing the step 2 from your suggestion, but initially couldn't replicate the results intended by my original suggestion.

I ran this code to test the VonMises distribution.

```python import jax import jax.numpy as jnp from jax import random import numpyro import numpyro.distributions as dist from numpyro import handlers from numpyro.infer import MCMC, NUTS from numpyro.infer.reparam import Reparam import arviz as az import matplotlib.pyplot as plt NUM_CHAINS = 10 numpyro.set_host_device_count(NUM_CHAINS) class CircularReparam(Reparam): def __call__(self, name, fn, obs): original_fn = fn fn, expand_shape, event_dim = self._unwrap(fn) # Draw parameter-free noise. new_fn = dist.Normal(0, 1).mask(False) # arbitrary, improper uniform value = numpyro.sample( f"{name}_unwrapped", self._wrap(new_fn, expand_shape, event_dim), obs=obs, ) # Differentiably transform. # value = jnp.fmod(value, 2 * math.pi) # in [0, 2 * pi) # or maybe this? value = jnp.fmod(value + math.pi, 2 * math.pi) - math.pi # in [-pi, pi) # or this (original suggestion)? # value = jnp.arctan2(jnp.sin(value), jnp.cos(value)) # Simulate a pyro.deterministic() site. numpyro.factor(f"{name}_factor", original_fn.log_prob(value)) return None, value num_warmup, num_samples = 1000, 1000 @handlers.reparam(config={'phi': CircularReparam()}) def model(): phi = numpyro.sample('phi', dist.VonMises(3.0, 4.0)) rng_key = random.PRNGKey(10) rng_keys = random.split(rng_key, NUM_CHAINS) # Split key for each chain # Sample using NUTS kernel = NUTS(model) mcmc = MCMC(kernel, num_warmup=num_warmup, num_samples=num_samples, num_chains=NUM_CHAINS) mcmc.run(rng_keys) # Create trace object for plot trace = az.from_numpyro(mcmc) # Plot trace az.plot_trace(trace) plt.savefig("trace_test.png") ```

When I use jnp.fmod to get from -pi to +pi the resulting trace looks like this:

When I instead use the arctan2 pseudoinverse (commented out in the code) the trace looks more like what I expect:

I am speculating, but could this difference be to do with the differential of fmod behaving differently compared to arctan2?

Note: I think that implementing this the way you suggest doesn't require a new Circular constraint, because the VonMises distribution already uses the interval constraint from -pi to +pi. Unless it would still be useful for "completeness".

...register the new circular constraint and transform with transform_to() but not biject_to(), and I think we'll want to add a new improper distribution called say Sinusoidal or ImproperSinusoidal or something.

[fritzo]

@alexlyttle looks great! Sorry about my error in trying to simplify arctan2(sin(x),cos(x)), I was trying to avoid the relatively expensive transcendental functions. How about instead np.remainder(x+pi,2*pi)-pi? It looks like that version is correct and cheap:


I think that implementing this ... doesn't require a new Circular constraint

Oh good point. I think we could go either way here: it would provide semantic information, but not yet be exercised. I defer to you as to whether to implement it. Our longer-term plans include adding automatic reparametrization support, and that would be easier if we could inspect and see your Circular constraint, so in the longer term I think Circular would be nice to have.

[alexlyttle]

@fritzo jnp.remainder works just fine, I forgot that fmod(-x) == - fmod(x) too! Good thinking regarding using a cheaper alternative, I hadn't considered that.

Oh good point. I think we could go either way here: it would provide semantic information, but not yet be exercised. I defer to you as to whether to implement it. Our longer-term plans include adding automatic reparametrization support, and that would be easier if we could inspect and see your Circular constraint, so in the longer term I think Circular would be nice to have.

I am happy to make a Circular constraint if it helps out in future. The way I did it in my hacked solution was something like,

class Circular(constraints._Interval):
        def __init__(self):
                super().__init__(-math.pi, math.pi)

circular = Circular()

and then VonMises.support = circular. As it stands, this does nothing on its own, but like you say it may be useful later.

I can make a PR with what I have so far and will tag this Issue. We can carry on this discussion there or whatever is easier for you.

[fritzo]

Sounds good. If you do make a Circular constraint, I'd avoid inheriting from _Interval because that might trigger the SigmoidTransform which would lead to poor mixing behavior as you've observed. It's safer to directly inherit from Constraint.

[fehiepsi]

Thank @alexlyttle for stimulating the discussion and working on a solution.