QIP-9: Change difficulty adjustment algorithm to cause less swings in block time

Earlz commented 5 years ago

Right now the block time of the Qtum network has been observed to have a cyclic "sway" of long and short blocks. JB has done extensive analysis on this problem complete with network simulation and has found the rather complex cause, as well as a solution. This QIP proposes to use his solution. This would require a hard fork

JB395 commented 5 years ago

The Problem

The Qtum retargeting algorithm which sets the difficulty of mining each new Proof of Stake block is wrong. This causes two problems 1) occasional long spacings between blocks (30 – 40+ minutes) and 2) the whole blockchain is running about 12% slow (144 seconds block spacing vs. should be 128 seconds by design) which means 12% lower TPS, block rewards, halving, etc. Because the difficulty is a consensus parameter, it will take a hard fork upgrade to fix.

The long spacings between blocks are caused by a sequence of fast blocks (< 128 seconds) pushing the difficulty too high. It is not deterministic that these short block sequences will produce a long block, but they have once a month, or more. A recent example is block 303,994 on January 20, 2019, at 16:54:24 UTC, which had a spacing of 46 minutes and 8 seconds.

This table shows the lead up to this slow block, with the short block sequence starting at block 303,983:

Block 303994 Table

For 200 blocks bracketing this slow block the average difficulty was 3.26 million. Block 303994 had a difficulty about 3.33 times the average.

Difficulties for blocks 303,890 to 304,089 are shown in the chart below, with the average (dashed green line). Notice the sequence of short blocks starting about block 303,983 pushing up the difficulty.

2019-21 Blocks 303890 - 304089

Reviewing the slow Mainnet blocks in the range 6,000 to 307,800 gives these results:

Longest block spacings

This means, on average, each month there are 20 blocks with spacing greater than 20 minutes.

The Solution

Retargeting Multiplier

The solution is to fix the retargeting algorithm which adjusts the target for every new block. The algorithm calculation is made at pow.cpp line 92 – 93, essentially

newTarget = previousTarget * (targetMultiplier + actualSpacing + actualSpacing) / (targetMultiplier + 256)

the actual code is

                bnNew *= ((nInterval - 1) * nTargetSpacing + nActualSpacing + nActualSpacing);
                bnNew /= ((nInterval + 1) * nTargetSpacing);

This gives an exponential moving average, since the numerator has an addition for two times the block spacing, while the denominator has an addition for two times the target block spacing (or 256 seconds). If the block spacing is 128 seconds the target multiplier will be 1.0 and the target will be unchanged. If the block spacing is < 128 (block was faster than the desired spacing of 128 seconds), the target multiplier will be < 1.0, the new target will be lower, making it, on average harder (longer) for the next block.

The retargeting formula is easy to calculate but causes wrong average block spacing. Academic papers for discrete-time queueing response show curved response graphs, while this formula gives a straight-line response. By introducing an additional multiplier of 1.067 for spacings greater than 128 seconds (essentially bending the response curve for slower blocks) the average block spacing for the 832 multiplier can be placed at 128 seconds:

feedback curve 832

I do not propose this solution because the 832 multiplier is still too aggressive and leads to runs (for faster than target spacing blocks) pushing the target way down, which causes slow blocks as shown above.

Instead, the solution is a much higher target multiplier of 20,000, which when used in the numerator and denominator of the retargeting algorithm gives a much gentler adjustment of the target. With a 20,000 target multiplier, the feedback curve looks like:

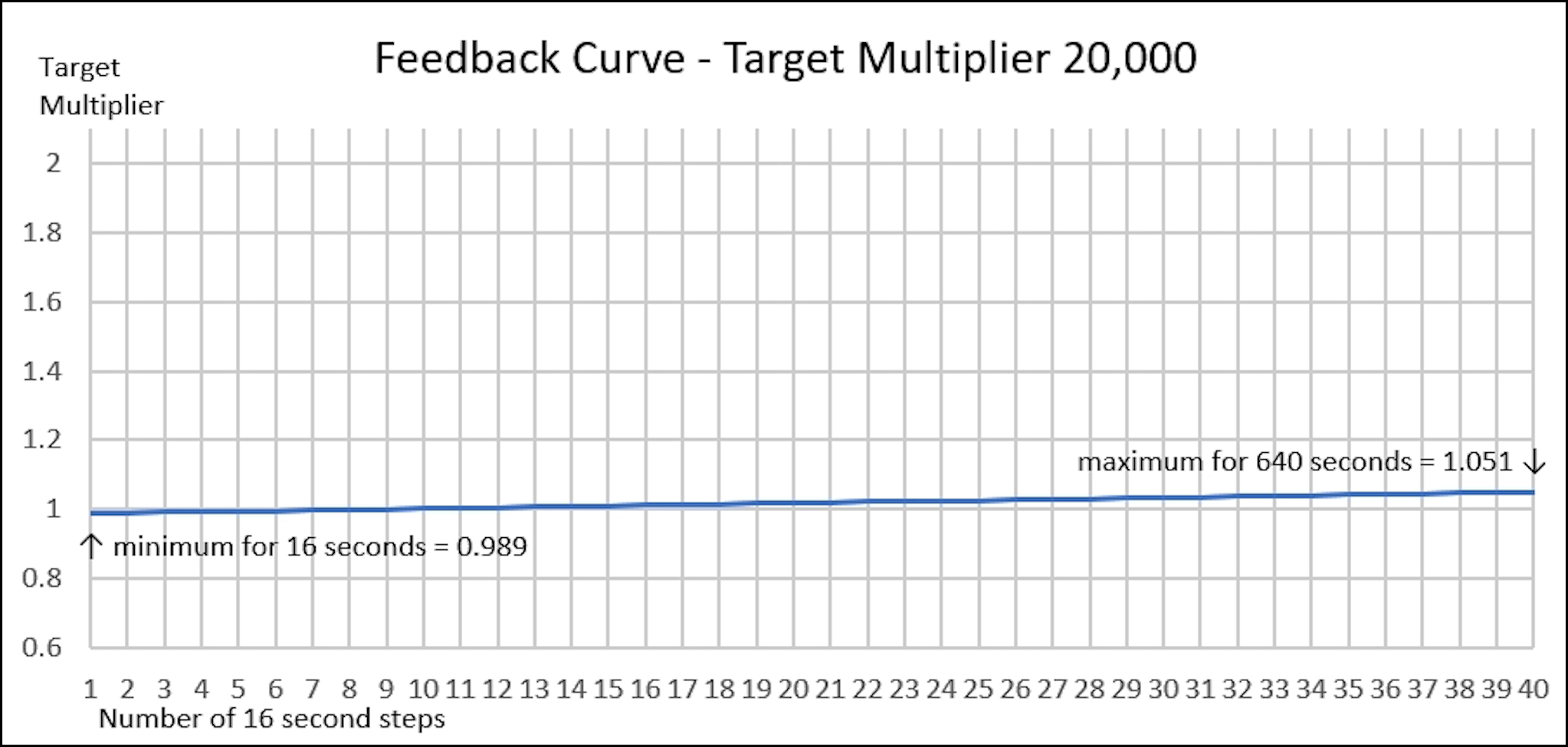
feedback curve 20000

I chose the 20,000 value for the new target multiplier after many simulations. Using the retargeting calculation (without any additional factor for slower blocks) where the retargeting multiplier is varied from 400 to 80,000 gives this chart for average spacing:

5k wallets 20k blocks

20,000 blocks in the chart above represents about one month of real time, but takes several days to simulate. We can get better averages with more blocks (and less wallets – probability says the results must be the same), here 3 wallets for 5 million blocks (about 20 years real time):

3 wallets 5m blocks

Finally, a chart of simulation results which includes a tally of slow blocks > 640 seconds and the slowest block (Max Seconds) as the target multiplier value is adjusted from 400 to 80,000 (with 5,000 wallets for 20,000 blocks): target multiplier table

Network Weight Fix

The 2nd fix is to remove unnecessary variation in the network weight calculation. Network weight is a short term SMA (simple moving average) of recent difficulties divided by a SMA of recent block spacings:

network weight formula

Network weight is used only to calculate time to expected reward. Using a sum of block spacings in the denominator (as opposed to a fixed denominator) provides no useful information for this interval given the amount of randomness in the retargeting algorithm, and causes large jumps in network weight when a long spacing enters (or leaves) the average.

For example, a block spacing of 20 minutes (which will still happen with the changes in step 1) will cause an instant drop of 10% in network weight, followed 72 blocks later by a 10% jump when the long spacing leaves the moving average.

The chart below shows simulated results (5,000 wallets, 2,000 blocks, retarget multiplier 20,000, true network weight 19.2 million) for the current Network Weight and the New Network Weight (fixed denominator and corrected scaling factor):

network weight 02-04-2019

There will always be variation in network weight due to random block spacing, but using a fixed denominator reduces the variation spikes.

xuanyan0x7c7 commented 5 years ago

It's better to use exponential adjusting against linear adjusting.

The key point of difficulty adjustment algorithm is src/pow.cpp#L91-L93, we write it as a clearer form:

$\frac{T_{n+1}}{T_n} = 1 + \frac{t_n-128}{K}$

where T_n is the target of block n, t_n is the interval of block n.

We introduce a new difficulty adjustment algorithm which has the form

$\frac{T_{n+1}}{T_n} = \exp \left( \frac{t_n-128}{K} \right)$

Exponentials are used in the equation because it's easy to multiply together. From this equation we get

$\frac{1}{n} \sum_{k=1}^n t_k = 128 + \frac{K}{n} \ln\frac{T_{n+1}}{T_1}$

The left term is the average block interval, from the equation above, when n is big enough, the average block interval equals to 128.

Here is the comparison between two algorithms of different K:

K	Average (Old)	Slow Blocks (Old)	Average (New)	Alow Blocks (New)
200	191.49	5.82%	128.1648	2.62%
300	161.30	3.51%	128.0262	1.96%
400	150.69	2.58%	128.0064	1.62%
500	145.24	2.11%	128.0023	1.43%
600	141.85	1.82%	128.0010	1.30%
800	137.99	1.49%	128.0003	1.14%
1000	135.84	1.32%	128.0001	1.05%
1500	133.07	1.11%	128.0000	0.93%
2000	131.74	0.99%	128.0000	0.88%
2500	130.96	0.93%	128.0000	0.85%
3000	130.46	0.89%	128.0000	0.82%
4000	129.84	0.86%	128.0000	0.79%
5000	129.46	0.83%	128.0000	0.78%
6000	129.22	0.80%	128.0000	0.77%
7000	129.04	0.79%	128.0000	0.76%
8000	128.91	0.78%	128.0000	0.75%