Push-based query invalidation

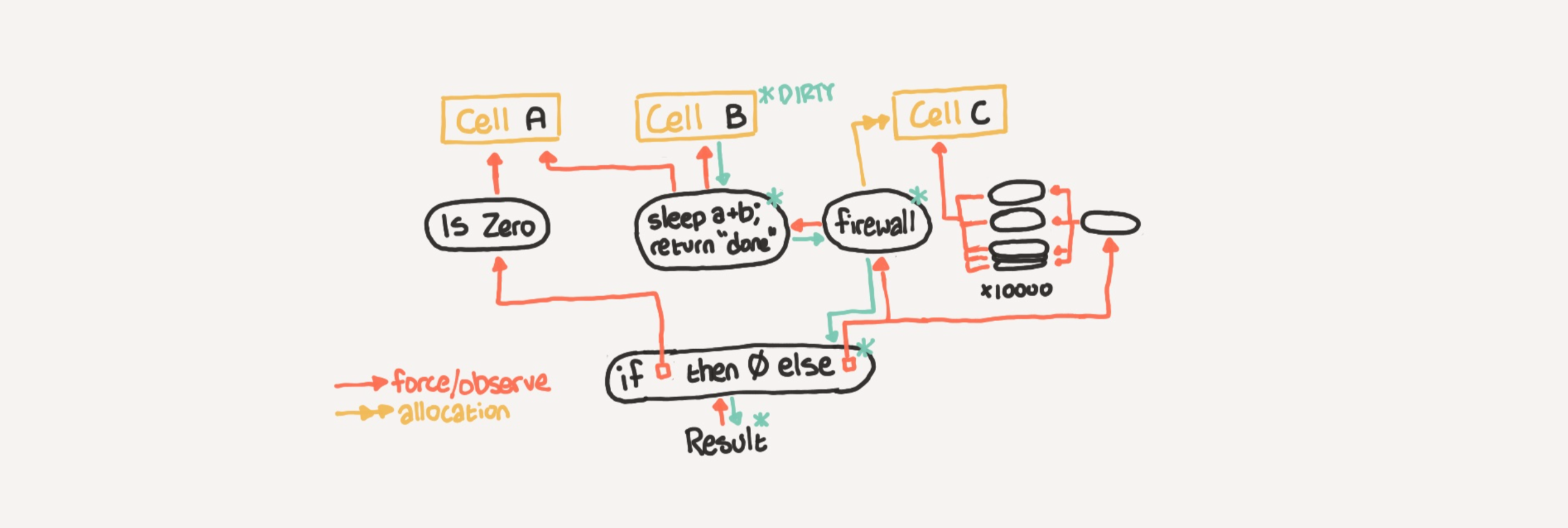
Currently, applying any change advances the global revision and "marks" all queries as potentially invalid (because their verified_at becomes smaller than current revision). The "marking" process is O(1) (we only bump one atomic usize), but subsequent validation can be O(N). Validation is on-demand (pull-based) and cheap because we don't execute queries and just compare hashes, but it still must walk large parts of the query graphs.

Here are two examples where we might want something more efficient.

function body modification

In IDEs, a lot of typing happens inside a single function body. On the first sight, this seems like it could be implemented very efficiently: changing a body can't (in most cases) have any globally effects, so we should be able to recompute types inside function's body very efficiently. However, in the current setup, types inside functions indirectly depend on the all source files (b/c, to infer types, you need to know all of the impls, which might be anywhere), so, after a change to a function, we need to check if all inputs are up to date, and this is O(N) in the number of files in the project.

unrelated crates modification

Suppose we have two independent crates, A and B, and a third crate C, which depends on A and B. Ideally, any modification of A should invalidate queries for C, but all queries for B should remain fresh. In the current setup, because there's a single global revision counter, we will have to re validate B's queries anyway.

It seems like we could achieve better big-O here, if we move validation work from query time (pull) to modification time (push).

In the second example we, for example, can define a per-crate revision counter, which is the sum of dependent-crates revisions + the revision of crate's source. During modification, we'll have to update the revision of all the reverse-dependencies of the current crate, but, during query, we can skip validation altogether, if crate-local revision hasn't change.

In the first example, we can define a "set of item declarations" query, whose results should not be affected by modification of function bodies. As "set of all items" is a union of per-files set of items (more or less, macros make everything complicated), we should be able to update when a single file is modified without checking if all other files are fresh.

This is one of the key differences between salsa and adaption (cc @matthewhammer). We followed here the Glimmer approach (cc @wycats) — in part because it is much simpler. You only need to track the inputs to any query, and don't have to be able to work the graph the other way. In the context of glimmer, it was also found to be more efficient: you are only doing work you know you have to do.

I think I would like to wait a bit until we see a true problem before pre-emptively making changes here. That might reveal whether indeed any changes are needed.

I would expect that in the context of an IDE, as you type into a fn, the IDE is also prioritized re-evaluation of queries related to that function, so they need to be re-evaluated anyway. It will also be re-evaluating the set of errors in other files, of course, but that can be done at a lower priority and will be continuously getting canceled as you type. Once you reach quiescence, we'll have to revalidate the inputs to those other files, but I expect that will be fast. In particular, they will share many of the same inputs, so the idea of O(n) time to revalidate a single query isn't really correct -- don't forget that once we revalidate the work for a given function, we cache that by updating verified_at, so we won't revalidate it twice. Hence it's really O(n) time to revalidate the entire graph.

But I guess time will out. =)

100% agree that the current approach might turn out to be just fast enough!

Hence it's really O(n) time to revalidate the entire graph.

That's true yeah, but, OTOH, it's one of the main optimization of IDEs that they avoid showing errors in other files. It's interesting that VS Studio with roslyn, has an "whole solution analysis" checkbox, which controls "show errors in all files" behavior. It is on by default (all errors are shown), but docs suggest disabling it for large projects. I wonldn't be surprised if in Rust, due to the strong compilation boundaries between crates, we will be able to just always show all errors, regardless of the project size, as long as it is split into crates of manageable size.

I'm interested to see how well other points in the design space of "cache invalidation" play out in practice. The approach taken by salsa-rs (and glimmer) seems like an interesting one, and comparable to, but distinct from, the approach taken by Adapton.

@nikomatsakis characterizes Adapton accurately above: When a cell changes value, the Adapton runtime system eagerly dirties all of the thunks that observed the prior value (actually, it dirties the edge on which each observation is recorded; thunks are "dirty" when they have one or more dirty edges). To maintain its internal invariants about what is dirty and what is clean, Adapton also dirties the observers of thunks with dirty edges, transitively. Because this traversal is eager, however, it can also "short circuit" when it encounters an edge that is already dirty.

The logic for this traversal is currently implemented here: https://docs.rs/adapton/0.3.30/src/adapton/engine.rs.html#1306

(This OOPSLA 2015 paper discusses how it works formally, including the graph and its invariants: https://arxiv.org/abs/1503.07792)

In practice, this ("naive"?) approach to dirtying can be problematic for several reasons. We address most of these with refinements to the approach (also implemented above):

First, when "long chains" of dependencies arise, it is not practical to dirty and clean these long chains, since the traversals are too expensive. The general strategy here is not to change the Adapton runtime system itself, but instead to refactor the program (and thus, its dependency graph) by introducing a "firewall" (or more typically, a "chain of firewalls"). Each "firewall" consists of a named reference cell, whose (fixed) pointer address is returned from a memoized thunk, rather than the (changing) value contained in this reference cell. Later in a dependency chain, other thunks read the reference cell, and create an "indirect" kind of dependency between the producer thunk and the consumer thunk. A more detailed explanation and example are here: https://docs.rs/adapton/0.3.30/adapton/#nominal-firewalls

Second, sometimes a reference cell will hold a tuple (or some other "structured value"), and the thunks that depend on this result only inspect one projection of this value, and do not depend on the entire (aggregate) value. In this case, dirtying the dependencies naively may dirty too much. To overcome this issue, Adapton permits observations that carry (pure) mapping functions; the dirtying logic mentioned above uses these pure mapping functions to perform comparisons after mapping the observation. Here are some concrete examples of using this feature: https://docs.rs/adapton/0.3.30/adapton/#use-force_map-for-more-precise-dependencies

@matthewhammer all this reading has been really fantastic for my own learning, thanks so much for the links! i'm curious about the differences between firewalls vs incremental's node height approach — you mention in the adapton docs that

some other change propagation algorithms base their re-execution schedule on "node height" (of the graph's topological ordering). These algorithms may also have undesirable behavior. In particular, they may re-execute the division div in step 2, though it is not presently in demand. For an example, see this gist.

but it seems like a firewall-style approach could just as easily accidentally force! a dirty dependent firewall cell to recalculate that isn't in demand?

Thanks @lord; I'm very glad to hear that this information was interesting and useful to you.

but it seems like a firewall-style approach could just as easily accidentally force! a dirty dependent firewall cell to recalculate that isn't in demand?

The issue with the node height appoach is that it's simply not semantically meaningful: It has no relationship to the actual evaluation order of the original program, and consequently, the "incremental semantics" of the program can be wrong, especially around conditional control flow. The division-by-zero example tries the demonstrate the simplest version of that (very general) issue with JaneStreet Incremental.

If I understand the concern about the "firewall" mechanism, you're saying that in the role of the outside (non-cached) layer of the computation, we may not understand the true nature of the cached dynamic dependencies (and firewalls), and may mistakenly either:

Request work (via force) that we do not strictly need to do, thus wasting resources, but not affecting the values in the final outcome or the validity of the cached info, or
Request work we do not need to do, and do it "out of order" in a way that trashes the meaning of the results and/or cached info, and may also invalidate the dependency graph that tracks how these things inter-relate.

(IIUC, you're not thinking about the first concern, which is addressed by caching thunks' results and not redoing them unless they are dirty; that's the basic function of Adapton, so in those cases there's no wasted resources, beyond some minimal check to discover that the re-computation is not necessary.)

The second concern is about a more complex situation, and it assumes that we can jumble the order of the program's cache effects in a way that screws things up. This is a real concern.

But, we can mitigate this issue by adding a big coarse-grained thunk to wrap the steps that need to be encapsulated and (incrementally) repeated as a unit; the thunk represents this unit in the DCG, and by demanding it, rather than its individual substeps, we can avoid reordering steps in a way that jumbles the meaning of the cache effects.

Of course, it's okay if there are several course-grained thunks, and it's even okay if they share dependencies.

BTW: I recently rewrote a fresh version of Adapton in Motoko.

Here's that implementation's version of that "division by zero" example: https://github.com/matthewhammer/cleansheets/blob/master/test/simpleAdaptonDivByZero.mo

I'm happy to answer questions about the code. (FWIW I'm considering a Rust port of this new implementation, but it has not yet happened.)

Wow, thanks for the thorough and extremely rapid reply @matthewhammer! My concern was more 1 than 2, although now that you mention it incorrect results definitely would be bad!

Maybe it would help to illustrate my question with a contrived, but specific example? I'm really not 100% sure I even grok how firewalls work, so maybe this will be good to reveal my misunderstanding.

The example above resembles the division by zero example, but here the cost Incremental pays is time (instead of throwing an exception) by unnecessarily executing the very slow 'sleep' thunk when Var A switches from 2 to 0. However, although Adapton doesn't ever execute the sleep thunk unnecessarily, it does repeatedly update the dirty bit on those 10,000 thunks as A switches back and forth. So we can add a firewall in front of them:

Now, any time we calculate Result, we first force!(firewall) to make sure Var C is up-to-date, and we no longer repeatedly update the dirty bit on 10,000 thunks. But my understanding is we now have the same problem as Incremental, where if Var A switches from 2 to 0, we will unnecessarily execute the sleep thunk, right?

My vague understanding of Incremental is it also will bit-thrash on the 10000 nodes, but instead of the dirty bit, it's the 'observed' bit thrashing when Var A switches back and forth from 0 to 2? But this at the very least has the advantage that if Var A is 0 and Var B keeps changing, the sleep thunk will never refire.

Also would be curious if it's possible for the node height technique to actually generate incorrect results. My understanding is that its main issue is it may recalculate a thunk multiple times, and could throw exceptions that wouldn't otherwise, but when the calculation finally stabilizes (assuming no exceptions were thrown) it would have a consistent result? But again to emphasize my own inexperience — I really don't know what I'm talking about, and could just be confused about the algorithms

Nice pictures! Great question.

To make sure that I understand the intention of the graph illustrated here, it'd be helpful if we could map it more closely to the "demanded computation graph" (DCG) concept from Adapton.

To do that, we need to distinguish "thunk" nodes versus "ref" nodes (e.g., rounded versus square corners?) and writing/allocation edges versus forcing/demanding/observing edges (e.g., double-headed versus single-headed?). Most systems do not impose these distinctions, but they are each relevant for Adapton's dependence graph semantics.

Finally, when I draw the direction of edges, I usually draw all edges as going from the thunk that does the recorded edge action to the thunk (or ref) that receives that action.

So that means that demand edges indicate the direction that is communicating demand, and opposite from the flow of the eventual information-flow of the result of this demand. I think your pictures use the information-flow direction, and in some cases, do not indicate the original demand. This is pretty typical of data-flow diagrams, but it means that they are still ambiguous for our purposes here.

If I am reading this right, I think the only relevant "alloc" edge here is for the firewall, where the "firewall" node does the alloc/overwrite on Var C. The other edges all indicate how demanded values flow (but not necessarily what nodes demand them to run). Correct me if that reading is mistaken.

So, what's missing and thus still not clear to me is what node demands that this firewall ever execute the first time around? Again, if this picture is to be interpreted as an Adapton DCG (demanded computation graph) then every thunk node should either be a root of demand, or it should be rooted by one that demands it, perhaps transitively.

If you answer the question of what demands each node run initially (including the firewall), that answer also helps answer the question of what steps would precipitate the firewall being affected (and refreshed) in the future. It's okay if there is more than one way to re-trigger the "firewall" step that writes Var C. However, there cannot be zero ways. The graph you have now has no root of demand at all, and thus is not (yet) well-formed; so, there is no way (yet) of relating that step to the other steps (e.g., the conditional step that produces the final result) in terms of evaluation order. The information flow edges do not suffice on their own. FWIW, I believe this fact about dataflow graphs contributes to systems like JaneStreet being easily confused about re-execution semantics. We need a bit more structure to disambiguate things.

For instance, if the node Firewall is demanded ("called"/"invoked") by the If node (or else some wrapper thunk that demands this If and the Firewall steps), then this node would act as a root of demand and would encapsulate all of their demanded steps (transitively), preventing them from getting reordered or otherwise separated and jumbled up.

[Note that unlike JaneStreet's system, Adapton has no special "root of demand" status for a thunk; instead, it's just a property of the thunk not having any thunks depending on it, and it can change freely as the graph is enlarged with more structure (or shrunk, as needed).]

My understanding is that its main issue is it may recalculate a thunk multiple times, and could throw exceptions that wouldn't otherwise, but when the calculation finally stabilizes (assuming no exceptions were thrown) it would have a consistent result? But again to emphasize my own inexperience — I really don't know what I'm talking about, and could just be confused about the algorithms

Yes, this summary all matches my understanding as well, but I should admit that I have been doing manual reasoning about JaneStreet's approach, not reasoning based on actual experimentation. I haven't poured over their implementation or used it myself.

However, years ago, my colleague @khooyp demonstrated a semantic issue with Incremental, but it was precisely the situation of the "divide by zero" example only to demonstrate the point (nothing more involved than that, IIRC). The core semantic "mistake" was what you say above: Rerunning recorded steps when they should not be rerun, since they are not truly "in demand" based on the current state of the input variables.

Oh, one other comment the utility of firewalls, in the context of your nice picture (the second one):

Yes this is exactly the idea. We want to avoid needlessly doing that x1000 work on the right-hand side of the firewall mechanism.

Critically, all of that to-be-avoided work depends on a changing value in Var C that we can compare quickly to test for changes. Importantly, this mechanism is useful because it's much cheaper to test Var C for changes than to recompute the work that depends on the value of Var C. If the costs were similar (e.g., if the size of the value of Var C was proportional to the work depending on it), there wouldn't be a point to using this firewall mechanism here.

(As a side note to the salsa folks — I think this discussion is relevant to push-based query invalidation, but happy to continue the chat in another place if you'd rather avoid the spam!)

I think get firewalls now, thanks for taking the time to walk me through it! Some updated diagrams in adapton style in case it's helpful to folks reading this in the future:

The (in retrospect, obvious) 'bit' I didn't grok before is that with this setup, the dirty bit from Cell B will still reach Result, due to the extra observation line from the if statement to the firewall thunk. I guess this whole thing works because the programmer knows ahead of time that those x10000 nodes will definitely force Cell C? In my previous mental model, our Result was the one that forced firewall, but since there's a conditional between Result and Cell C, we don't know for sure at that point if forcing firewall is necessary?

Re Jane St's Incremental: I'm sure you're already aware of this as well, but again for future readers who like me were confused, it seems like the divide by zero example's problem is caused by their bind's height update behavior:

The height requirement does not apply to nodes returned by [f] but not created by [f] -- such nodes depend on the bind in effect when they were created, but have no dependence on [t].

So if the div bind is created inside res's bind fun instead of outside, this "fixes" the issue, although I guess it's certainly not possible in many circumstances.

I think this off-topic "thread" has resolved; thanks to the salsa folks for hosting this conversation between myself and @lord. It may be helpful to them; it's definitely been helpful for me.

Some updated diagrams in adapton style in case it's helpful to folks reading this in the future:

Wonderful. Thank you for these updated drawings!

As a personal aside: I always wonder if other people are seeing the (dynamic) dependence graph structure that I am seeing when I write a wall of text like the stuff above. Since there are so many decades of dataflow graphs, incremental computing and spreadsheets, I always have a reasonable suspicion that I am talking past people when I talk about the definitions that are particular to Adapton's (relatively recent) variation on the usual definitions. It warms my heart to see the progression of your pictures here, since they convince me this isn't happening, at least this time. Thanks so much. :)

As a more technical aside: This conversation convinces me that Adapton (and every similar or competing technique) should have more (moving) pictures, and ones that are easily created in a systematic way from a running example. I have had many starts and false starts toward that end, but nothing quite like your pretty pictures above, sadly. This desire continues to be inspiration for me for future work, though. Cheers!

salsa-rs / salsa

Push-based query invalidation #41