Hello Wolfgang, Glad you've overall had a good experience with ripser.py so far!
Wow, this is quite an interesting case. Because in a metric space d(x, y) = 0 if and only if x=y, we never expect there to be zeros in the distance matrix. But I see why you would want to use them with trajectories to bully the filtration into adding the edges between subsequent points in time first. Unfortunately, zeros in a sparse matrix are interpreted to be infinity (edges that are never added). Because I can't think of a clean way to change the API to allow actual zeros in the sparse matrix (and because it may not be such a general thing to do), what I would recommend as a hack for the moment is to make the edges between t and t+1 a very small number, which is orders of magnitude below any other edges you have (so maybe something like 1e-14). That should get you basically the results you're seeing with dense matrices.
I hope that's a reasonable answer for now. I'm curious to see what you end up doing with time series, as I also do a lot of work on trajectories. Best, Chris
On Mon, Jul 8, 2019 at 6:53 AM Wolfgang Merkt notifications@github.com wrote:
Hi guys, Thank you very much for your hard work in developing and maintaining this excellent tool - it really is a breeze to work with!
We are currently working on problems involving time-series data (trajectories). In order to achieve this, we post-process the distance matrix D to set the distance between subsequent points (t and t+1) to 0. This works just fine with dense filtration and we obtain the results that we expect. With sparse/approximate filtration, however, this breaks (maybe because the 0 to be interpreted as a sparse entry?). As our datasets usually are larger than the synthetic ones we used to test, ripser.py often runs out of memory and we'd like to leverage the approximate filtration. Do you have any advice or perhaps best practices for dealing with time-series data and approximate filtration?
Thank you very much, Wolfgang
— You are receiving this because you are subscribed to this thread. Reply to this email directly, view it on GitHub https://github.com/scikit-tda/ripser.py/issues/78?email_source=notifications&email_token=AAJWDZUYRHB4N23C7NDQIG3P6MMBHA5CNFSM4H62NOF2YY3PNVWWK3TUL52HS4DFUVEXG43VMWVGG33NNVSW45C7NFSM4G52G5XQ, or mute the thread https://github.com/notifications/unsubscribe-auth/AAJWDZRKGJPA3XEW7HJ6HN3P6MMBHANCNFSM4H62NOFQ .
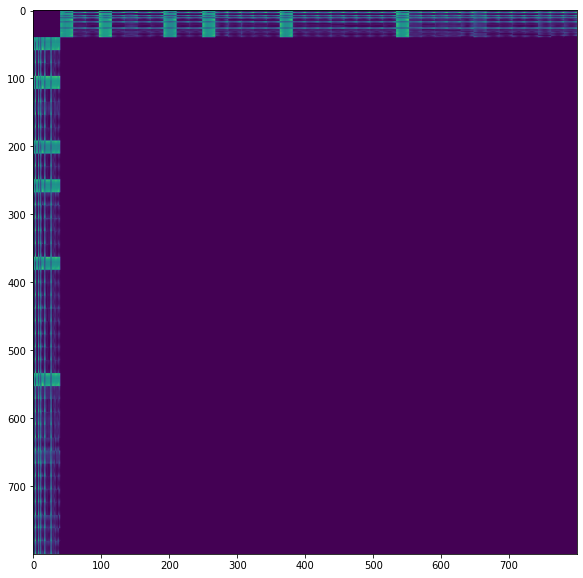
Hi guys, Thank you very much for your hard work in developing and maintaining this excellent tool - it really is a breeze to work with!
We are currently working on problems involving time-series data (trajectories). In order to achieve this, we post-process the distance matrix
Dto set the distance between subsequent points (tandt+1) to0. This works just fine with dense filtration and we obtain the results that we expect. With sparse/approximate filtration, however, this breaks (maybe because the0to be interpreted as a sparse entry?). As our datasets usually are larger than the synthetic ones we used to test, ripser.py often runs out of memory and we'd like to leverage the approximate filtration. Do you have any advice or perhaps best practices for dealing with time-series data and approximate filtration?Thank you very much, Wolfgang