Jhc-china
commented
2 years ago - I think the S has already been divided by 2pi? line 258 in Network.py is p[:, i] = self.atan2(v[:, 1], v[:, 0]) / self.tpi;
- I have the same question as you; the equation is confusing.
thyzju17
Hello Sebastian,
I''ve sent you email twice but have not recieved any response. I am not sure if there is any connection problem and I try to connect you via github issues.
I found there might be two mistakes in the paper.
In Eq. 5, the range of S should be (-pi, pi), so I think S should be out of the innermost scope: $A\cdot sin(2pi(F\cdot Tau-S)+B (5) -> A\cdot sin(2pi(F\cdot Tau)-S)+B (5.1) $, or divided by 2pi before passing it in Eq. (5). I found it hard to predict S to be similar to the curve in fig. 3 using Eq. 5 directly. I tested Eq. (5) and Eq. (5.1) and plotted the figures after training for 5 epoches. Eq 5:
Eq 5.1:
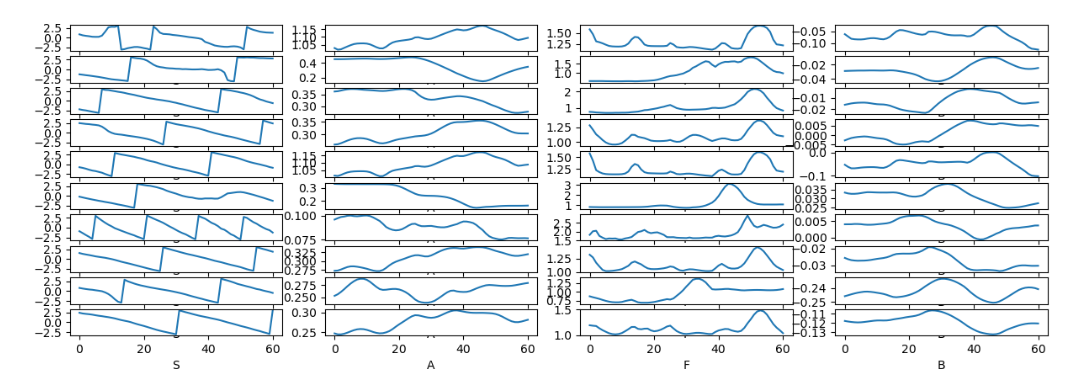
In Eq 9, the next phase is calculated by interpolating two phases, and multiply it by $A_{t+dt}$:
However, the phase $Pt$ and $P{t+dt}$ also contains the information about the amplitudes, so the expected prediction of $A_{t+dt}$ should be very similar to one, which means scale the interpolated result. I am not sure if the amplitudes should be predicted by the difference between two frames, just like the frequency does?
Besides, I am not sure how to handle the loss of the phase. I employ the mse loss between the predicted phase in eq 9 and the groundtruth phase, but the frequency of the predicted phase is inaccurate. Do we have to employ loss on the amplitudes and frequence additionally? Which method do you use?
I will appreciate it if you correct me if I am wrong. I look forward to hearing from you.
Best regards,
Xiangjun Tang