Honestly I made a lot of those just copying from older code I had, so if there are better ways to do it then I think we should make the improvements.
Closed skhrg closed 2 years ago
Honestly I made a lot of those just copying from older code I had, so if there are better ways to do it then I think we should make the improvements.
Yeah, when I get some time I will check to see what the difference actually is between the two for how we filter our data. If its around the standard float error level then we are probably fine, if its some non trivial difference we may want to make the switch. The annoying thing about using sos over ba or zpk is there is no freqs equivalent (there is a freqz equivalent but most of our filters seem to be analog) so its not exactly a nice drop in place replacement given how filters.py is written.
This may be a dumb question but why are the but why are low_pass_butter4 and high_pass_butter4 analog filters? My understanding is (discussion in #127 and #253 notwithstanding) that our data is regularly sampled and that with regularly sampled data digital is preferred over analog. But I am no filter expert so that may be incorrect.
Because digital filters are "real" / "causal," which means they add phase shifts to the data that are dependent on frequency. This has the affect of smearing out what we're looking at (just like timeconstants do). You'll notice that both our time constant and iir filters have complex transfer functions because we use those to deconvolve the causal filters applied data before it gets put on disk. The butterworth ones are all real valued, meaning they won't add any phase shifts.
Can you do digital non-causal filters? I don't think you can, but you could be proven wrong.
Ah that makes sense, thanks.
Can you do digital non-causal filters? I don't think you can, but you could be proven wrong.
I could be wrong but isn't that the point of functions like filtfilt? You apply the filter forwards and then backwards and it cancels out the phase shifts. Of course it also doubles the order of your filter so it's not always ideal.
Oh true, you're right. We can't design non-causal digital filters but can do things like that. If it's faster to run that then it is to zero-pad + FFT then it could be worth it.
From quick glance at the source for filtfilt it looks like it does some stuff to find initial parameters and whatnot and then just passes it off to lfilter twice. lfilter does a convolution to produce the output. So I think this is basically just zero-pad + FFT but twice which sould be ~2 times slower.
If one is going to use FFTs, then one doesn't really need the kind of fancy filter that is designed by scipy.signal -- you can draw whatever shape you want, in frequency space, and apply that to your FFTed data, then iFFT that result.
The point of these scipy.signal "iirfilter" things, with A and B coefficients (or the SOS form if you prefer), is that they also can be implemented in firmware or software, to operate in ~real time on digital data during data acquisition. That implementation doesn't involve an FFT -- it uses a few accumulators and some arithmetic operations to apply the filter (think of it as a fancy version of a rolling average or some other simple in-line smoothing function), yielding one output sample per input sample. The Smurf and MCE both use this kind of filter (though the MCE implements it in firmward, and the Smurf in software). These firmware / software implementations are necessarily "causal" -- they impart a phase lag that we remove in post-processing.
I am not sure what 'digital' and 'analog' mean, in scipy.signal ... but the 'analog' results seem the most straight-forward, mathematically... the 'digital' results seem to take into account a bunch of stuff one should worry about if you were going to implement the discrete case, in firmware (but I might be wrong). That's not a problem we need to worry about in the low_pass_butter4 and high_pass_butter4 functions; we just want those to provide some kind of ~smooth cutoff without phase lag. They seem to do that.
Thanks. I'm going to close this because based on this:
we just want those to provide some kind of ~smooth cutoff without phase lag. They seem to do that.
I don't think the numerical errors from using ba parameters over sos really matter for us. At least this issue functioned as a good refresher on filters for me.
I've noticed that our filtering functions tend to use ba parameters over sos or zpk to define the filter. For example: https://github.com/simonsobs/sotodlib/blob/c83dd75c95ed2a461a02847b5f650bb25afe9174/sotodlib/tod_ops/filters.py#L240
My understanding is that this is not recommended anymore due to numerical errors and we should be using sos instead. From the scipy docs:
They also have an example of the difference between them: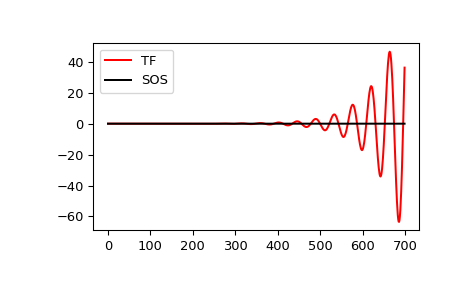
Should we move towards using sos over ba (at least where convenient) or are these errors below the level we care about?