解答:采用归并排序
归并排序采用了分治策略,将数组分成2个较小的数组,然后每个数组再分成两个更小的数组,直至每个数组里只包含一个元素,然后将小数组不断的合并成较大的数组,直至只剩下一个数组,就是排序完成后的数组序列。
对应于链表喃?
4->2->1->3第一步:分割
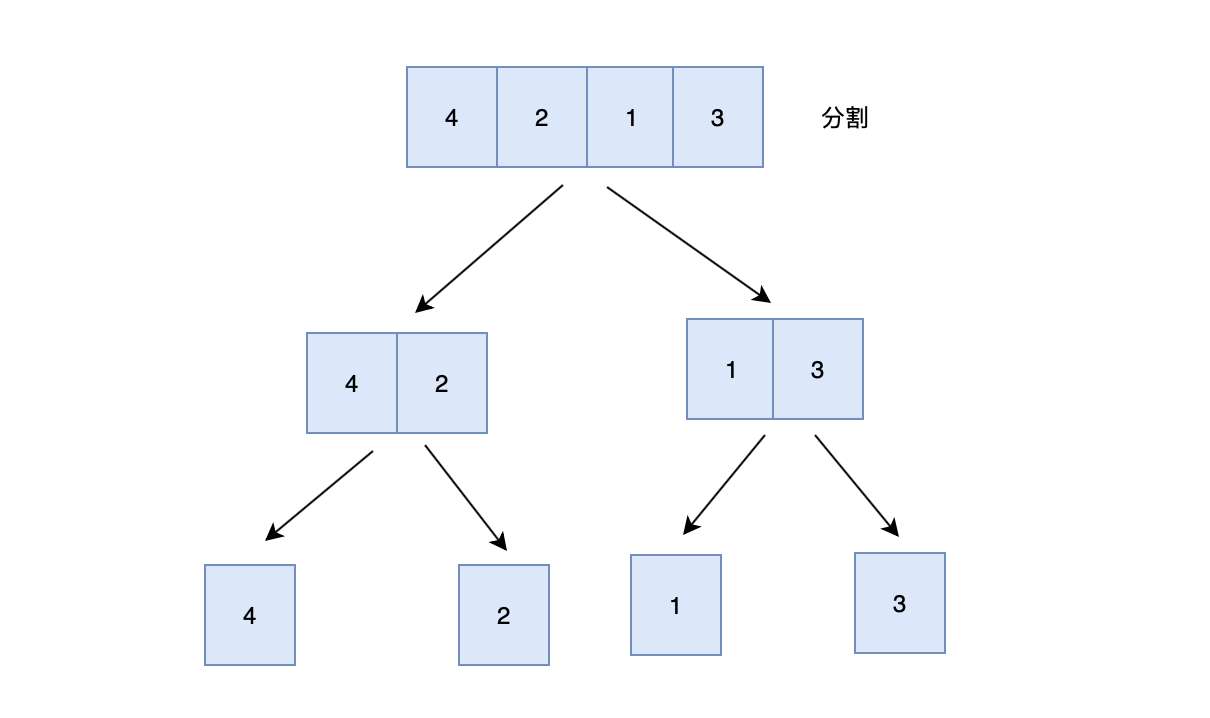
- 使用快慢指针(双指针法),获取链表的中间节点
- 根据中间节点,分割成两个小链表
- 递归执行上一步,直到小链表中只有一个节点
第二步:归并(合并有序链表)
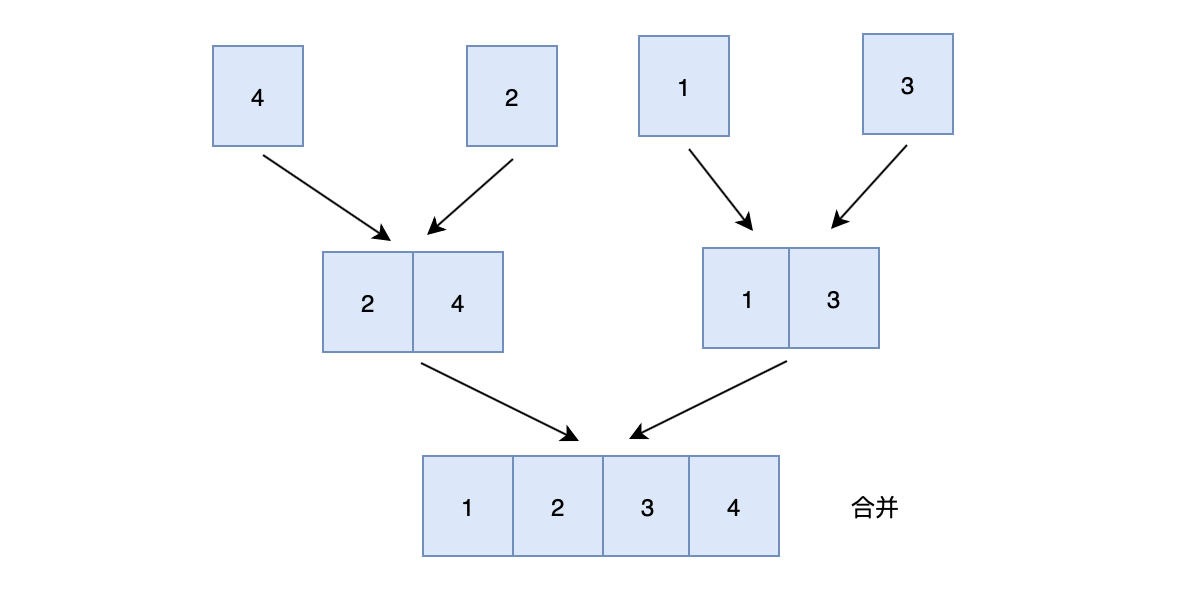
代码实现
let sortList = function(head) {
return mergeSortRec(head)
}
// 归并排序
// 若分裂后的两个链表长度不为 1,则继续分裂
// 直到分裂后的链表长度都为 1,
// 然后合并小链表
let mergeSortRec = function (head) {
if(!head || !head.next) {
return head
}
// 获取中间节点
let middle = middleNode(head)
// 分裂成两个链表
let temp = middle.next
middle.next = null
let left = head, right = temp
// 继续分裂(递归分裂)
left = mergeSortRec(left)
right = mergeSortRec(right)
// 合并两个有序链表
return mergeTwoLists(left, right)
}
// 获取中间节点
// - 如果链表长度为奇数,则返回中间节点
// - 如果链表长度为偶数,则有两个中间节点,这里返回第一个
let middleNode = function(head) {
let fast = head, slow = head
while(fast && fast.next && fast.next.next) {
slow = slow.next
fast = fast.next.next
}
return slow
}
// 合并两个有序链表
let mergeTwoLists = function(l1, l2) {
let preHead = new ListNode(-1);
let cur = preHead;
while(l1 && l2){
if(l1.val < l2.val){
cur.next = l1;
l1 = l1.next;
}else{
cur.next = l2;
l2 = l2.next;
}
cur = cur.next;
}
cur.next = l1 || l2;
return preHead.next;
}引入递归算法的复杂度分析:
- 递归算法的时间复杂度:递归的总次数 * 每次递归的数量
- 递归算法的空间复杂度:递归的深度 * 每次递归创建变量的个数
复杂度分析
- 时间复杂度:递归的总次数为 T(logn) ,每次递归的数量为 T(n) ,时间复杂度为 O(nlogn)
- 空间复杂度:递归的深度为 T(logn) ,每次递归创建变量的个数为 T(c) (c为常数),空间复杂度为 O(logn)
关于复杂度分析,请看这篇:前端进阶算法1:如何分析、统计算法的执行效率和资源消耗?
优化递归
使用迭代代替递归,优化时间复杂度:O(logn) —> O(1)
今天太晚了,明日更新🤦♀️
在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
示例 1:
示例 2:
附赠可测试leetcode链接:leetcode