An update on this issue:



By running the previous changes I got these results. Any suggestions on how to improve the accuracy of this problem?
I also tried running the 1D wave equation with a source term S(x,t)
def f_model(u_model, x, t):
c = tf.constant(1, dtype = tf.float32)
Amp = tf.constant(1, dtype = tf.float32)
frequency = tf.constant(1, dtype = tf.float32)
sigma = tf.constant(0.5, dtype = tf.float32)
source_x_coord = tf.constant(0, dtype = tf.float32)
Gaussian_impulse = Amp * tf.exp(-(1/(sigma**2))*(x-source_x_coord)**2)
S = Gaussian_impulse * tf.sin( 1 * tf.constant(math.pi) * frequency * t )
u = u_model(tf.concat([x,t], 1))
u_x = tf.gradients(u,x)
u_xx = tf.gradients(u_x, x)
u_t = tf.gradients(u,t)
u_tt = tf.gradients(u_t,t)
f_u = u_xx - (1/c**2) * u_tt + S
return f_uThe results shown are good but we can reach a lower L2 error value.

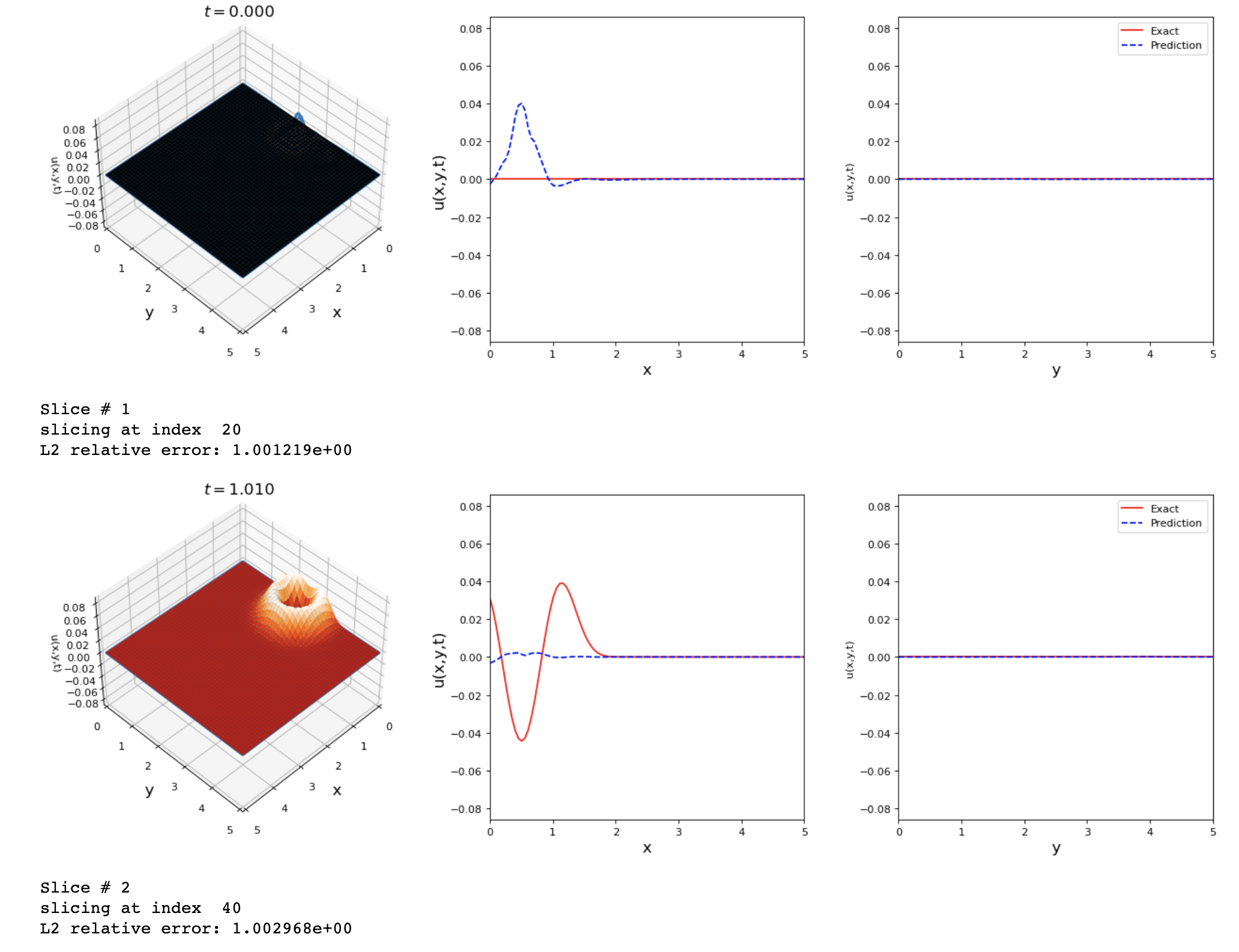
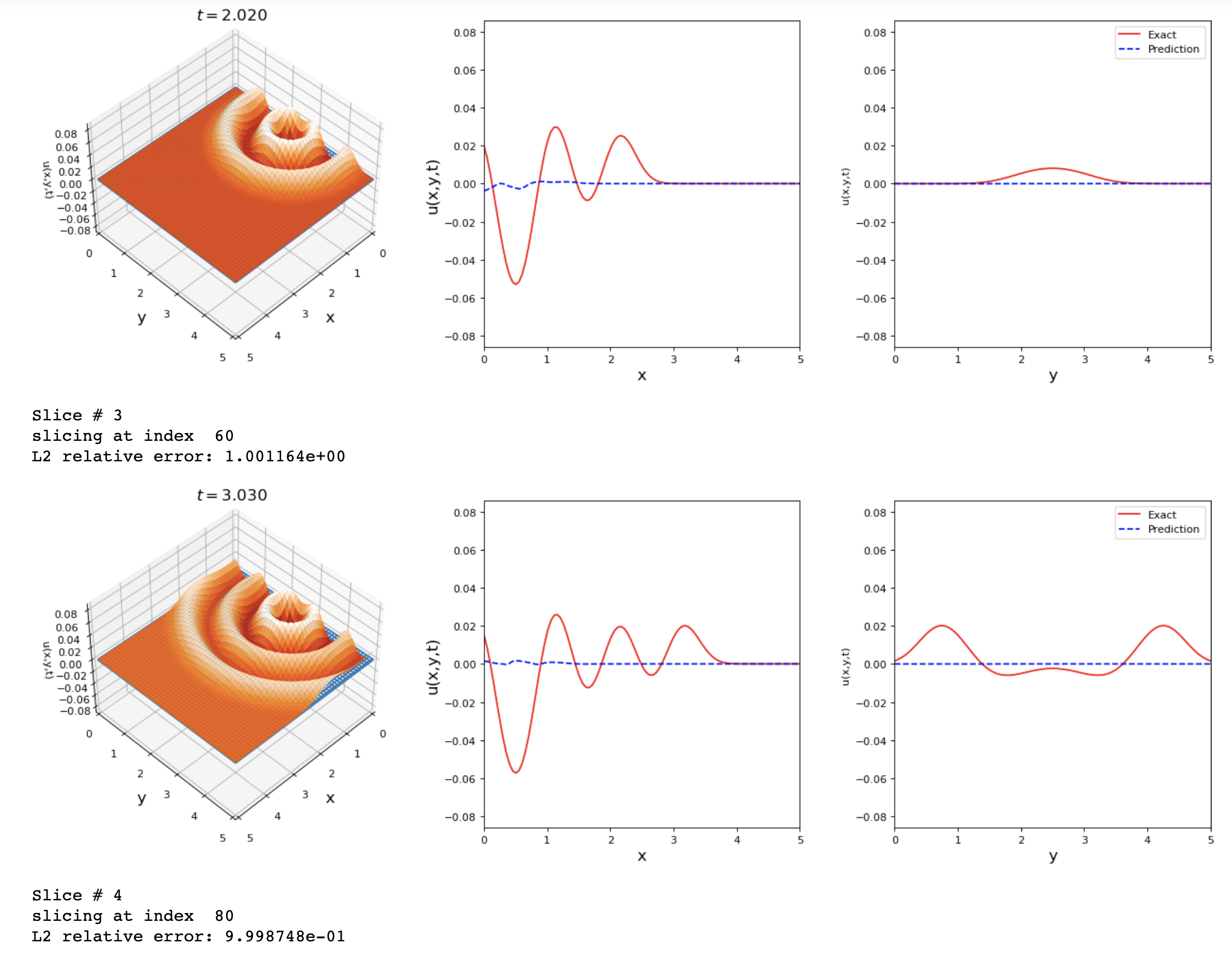
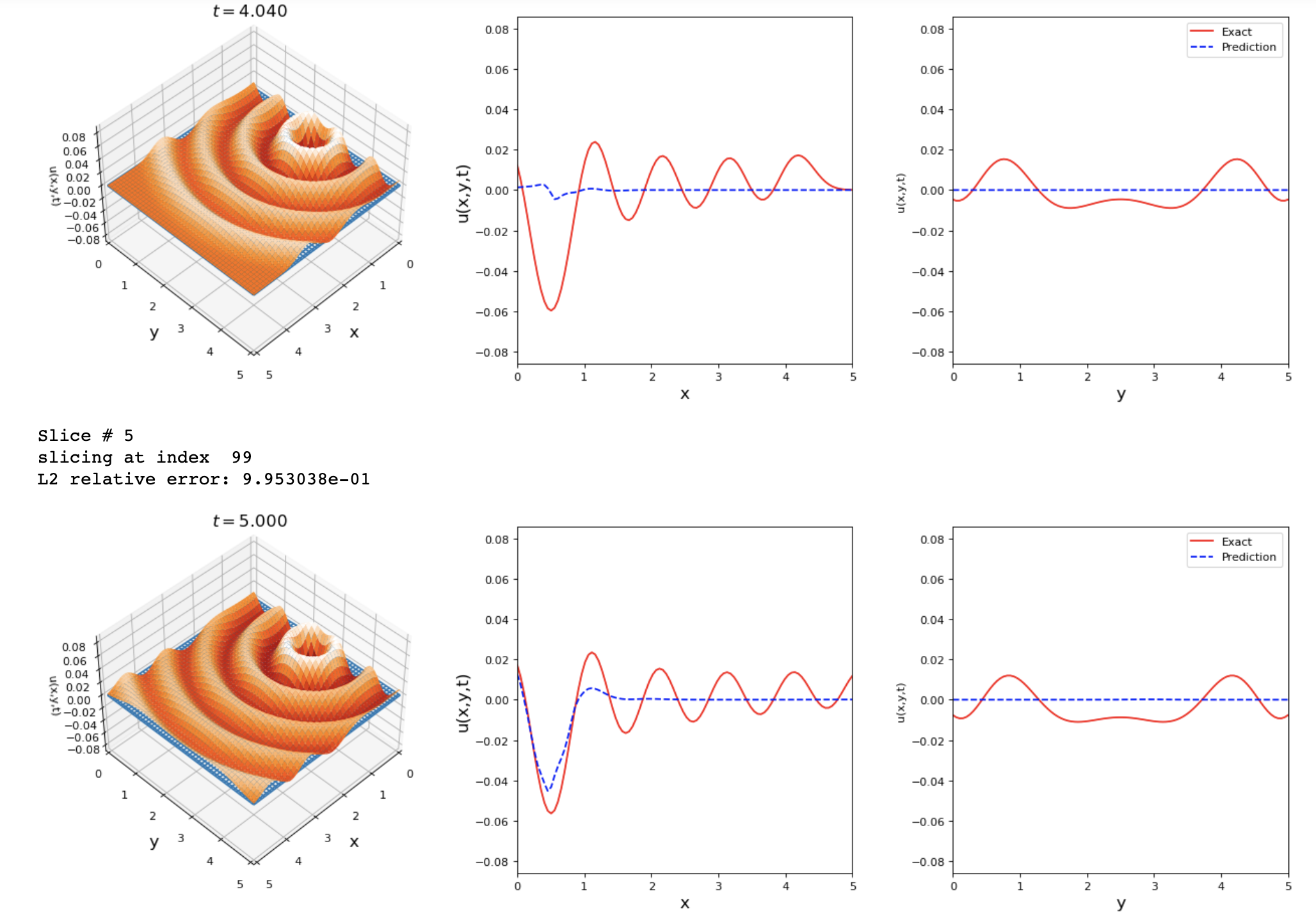
Thank you for the great contribution!
I'm trying to extend the 1D example problems to 2D, but I want to make sure my changes are in the correct place:
Domain = DomainND(["x", "y", "t"], time_var='t')
Domain.add("x", [0.0, 5.0], 100) Domain.add("y", [0.0, 5.0], 100) Domain.add("t", [0.0, 5.0], 100)
def func_ic(x,y): return 0
init = IC(Domain, [func_ic], var=[['x','y']]) upper_x = dirichletBC(Domain, val=0.0, var='x', target="upper") lower_x = dirichletBC(Domain, val=0.0, var='x', target="lower") upper_y = dirichletBC(Domain, val=0.0, var='y', target="upper") lower_y = dirichletBC(Domain, val=0.0, var='y', target="lower")
BCs = [init, upper_x, lower_x, upper_y, lower_y]
def f_model(u_model, x, y, t): c = tf.constant(1, dtype = tf.float32) Amp = tf.constant(2, dtype = tf.float32) freq = tf.constant(1, dtype = tf.float32) sigma = tf.constant(0.2, dtype = tf.float32)