Tensorflow 1.4.1 on Linux (CentOS-7.4) and Tensorflow 1.4.1 on MacOSX producing *very* different results in image creation simulation.

[Gemesys]

System information

• Have I written custom code (as opposed to using a stock example script provided in TensorFlow): No.

• OS Platform and Distribution (e.g., Linux Ubuntu 16.04):
  Linux CentOS-7.4 and MacOSx 10.10.5

• TensorFlow installed from (source or binary): Both; Installed from binary, then, built and installed from source. Same behaviour on each install.

• TensorFlow version (use command below): Tensorflow 1.4.0 and Tensorflow 1.4.1

• Python version: 2.7.14 (installed from binary, and then built and installed from source

• Bazel version (if compiling from source): Bazel 0.9.0. Source built and installed successfully, Python .whl file built & installed successfully.

• GCC/Compiler version (if compiling from source): Xcode7.2.1 and the Gnu gFortran, 5.2. (needed gFortran for SciPy install. All installs OK.)

• CUDA/cuDNN version: N/A - compiled and running CPU versions only for now.

• GPU model and memory:

• Exact command to reproduce: (See supplied test program - based on the Laplace PDE ("Raindrops on Pond") simulation example from Tensorflow Tutorial)

Description of Problem: I've run into a curious situation. I am getting very different behaviour in Tensorflow 1.4.1 on Linux and Tensorflow 1.4.1 on MacOSX, in straightforward image-generation simulation, based on the "Raindrops on a Pond" (Laplace PDE) example from the Tensorflow Tutorial.

I must stress that both Tensorflow installations seem to be 100% correct, and operate other tests correctly, producing the same numeric results for simple models.

I have also built Tensorflow 1.4.1 completely from source, and the Python 2.7.14 as well, on the MacOSX (MacBook) machine, in order to build the Python using "--enable-unicode=ucs4", since that was one difference I was able to find, between the two version. But even with the Macbook now running exactly the same Python 2.7.14 as the Linux box, I am still getting wildly divergent evoluationary behaviour as when I iterate the simple simulation. The numbers just zoom off in very different directions on each machine, and the generated images show this.

On the MacOSX, the simulation evolves very quickly to a pure white canvas (all "255"s), but on the Linux platform, the image grows more complex, with the generated numbers bifurcating between large negative and large positive - and hence when np.clip-ed, to range 0-255, show a complex moire-style pattern.

I have confirmed all related libraries and packages seem to be the same versions. The difference seems to be in the operation of Tensorflow.

This seems pretty serious, as each platform is Intel. The Linux box (CentOS-7.4) is Core-i3, while the Macbook is Core-i5. But both are 64-bit, and both Tensorflow installations seem to be correct. I have tried both the binary version, and then built a complete local version of Tensorflow 1.4.1 for the Macbook from source. Both seem to be Ok, and operate correctly. The Linux version of Tensorflow 1.4.0 was installed from binary appears to be operating correctly, albeit differently, but just for this one program.

When the sample program runs, it will display fourteen 400x400 images, as well as the numeric values of the row-20 of the "a" array (400 numbers). The program can be started from an Xterm shell window, with "python LapTest.py". It does not need Jupyter or IPython. With SciPy loaded, the images are rendered as .PNG files on both platforms, using Preview on the MacOSX MacBook, and ImageMagick on the CentOS-7.4 Linux box. Program runs fine to completion, and all looks ok on both machines.

But the results - even with the simple initial pseudo-random conditions - evolve completely differently, and consistantly. The Macbook version of Tensorflow 1.4.1 goes to a pure white screen, while the LInux Tensorflow 1.4.1 configuration evolves to a complex, chaotic, moire-pattern.

Leaving aside the question of even which machine is "correct", the expected result is of course that both machines should at least show clear evidence of similar behaviour.

No change was made to the test program, "LapTest.py", from one machine to the other. The different behaviour is not related to how the images are displayed, which is working fine on both platforms. A copy of this simple program is provided. I have removed or commented out the IPython/Jupyter dependent code, so this program can be run on plain vanilla Python 2.7.14, as long the appropriate packages (tensorflow, numpy, scipy, PIL (Pillow version), matplotlib, imageio ...) are available

Example of Source code to demostrate behaviour: LapTest.py

#-------------------------------------------------------------------------------
# Prgm: LapTest.py
#
# --- the Tensorflow LaPlace Image example (Uses PIL(Pillow ver.), and numpy)
# --- updated for TensorFlow 1.4.1 running on CentOS-7.4 & Python 2.7.14
#     compiled (configured, actually) with the "--enable-unicode=ucs4" option
#                                             (Python compile default is ucs2)
#                                             (which caused TensorFlow 1.4 to)
#                                             (fail to load. Building Python )
#                                             (with ucs4, => pip can install )
#                                             (TensorFlow 1.4.0 successfully.)
#
# --- This version of program tested on: MacOSX 10.10.5. (Yosemite)
# --- LapTest.py on Linux (CentOS-7.4), and LapTest.py on MacOSX, with Tensorflow-1.4.1 and
#     Python 2.7.14 (with ucs4 enabled on both Python versions), show *very*
#     different behaviour, and produce very different results.
#     Note: CentOS-7.4 is using Linux kernel: 4.14.9-1el7.elrepo.x86_64    
#
# --- Import various libraries for simulation
import tensorflow as tf
import numpy as np
import scipy.misc
import imageio
import os
import sys
import subprocess
import PIL
import time    

# --- Import for visualization and jpeg encoder  
import matplotlib
matplotlib.rcParams["backend"]= 'TkAgg'
from matplotlib import pyplot as plt
# from PIL import Image, ImageDraw
from io import BytesIO
#  from IPython.display import clear_output, Image, display

#--- we need this to get a sane for-loop...
def jump_range(start, end, step):
    while start <= end:
        yield start
        start += step

# --- function for displaying state of the pond's surface as an image
def DisplayArray(a, fmt='jpeg', rng=[0,1]):
  global proc
  # proc.kill() 
  # """Display an array as a picture. """
  a = (a - float(rng[0]))/float(rng[1] - rng[0])*37
  amod = np.clip(a, 0, 255)
  a = np.uint8(amod)
#  a = np.clip(a, 0, 255) 
#  a = np.uint8(a) 
#  np.clip(a, 0, 255, out=a )
#  a = a.astype('uint8')
  print " "
  print " ----------- This is a: => row 20  ------------"
  print a[20]
  print " ----------------------------------------------"
  f = BytesIO()
  # --- this is the cool, realtime thing that runs in Jupyter-IPython Notebook
  PIL.Image.fromarray(a).save(f,fmt)
  # --- clear_output(wait = True)  --- only for IPython
  # display(Image(data=f.getvalue()))
  # --- write the image
  # --- write the simulation images to .jpg files
  scipy.misc.imsave("tensor.jpg", a)
  pic = PIL.Image.open("tensor.jpg")
  # --- new approach... use subprocess, wait for time(2) then kill it
  # proc = subprocess.Popen(["display", "./tensor.jpg"])
  # time.sleep(0.5)
  pic.show()
  # clear_output(wait=True)
  # --- this line below doesn't work outside of the Jupyter environment...
  # display(Image(data=f.getvalue()))
  #
  # pic.close()  <--- does not work to close image.  Just removes the pointer to image in memory

def DisplayArrayToFile(a, fmt='jpeg', rng=[0,1]):
  # """Display an array as a picture to a file... """
  a = (a - rng[0])/float(rng[1] - rng[0])*37
  a = np.uint8(np.clip(a, 0, 255))
  f = BytesIO()
  # --- this is the cool, realtime thing that runs in Jupyter-IPython Notebook
  PIL.Image.fromarray(a).save(f,fmt)
  # clear_output(wait = True)
  # display(Image(data=f.getvalue()))
  # --- write the image
  # --- this is my stuff to write the simulation images to .jpg files
  #scipy.misc.imsave ("tensor_new.jpg", a)
  imageio.imwrite("tensor_new.jpg", a)
  # --- image = PIL.Image.open("tensor_new.jpg")
  # --- image.show()
  # clear_output(wait=True)
  # display(Image(data=f.getvalue()))
  #

# --- make print stmt print the whole array... (not just part of it...)
np.set_printoptions(threshold=np.nan)

# --- make interactive session for testing - can use regular session also
sess = tf.InteractiveSession()
# sess = tf.Session()

# --- computational functions go here... once we get jpeg pic working
def make_kernel(a):
  """Transform a 2D array into a convolutional kernel """
  a = np.asarray(a)
  a = a.reshape(list(a.shape) + [1,1])
  return tf.constant(a, dtype=1)

def simple_conv(x, k):
  """ A simplified 2D convolutional operation """
  x = tf.expand_dims(tf.expand_dims(x, 0), -1)
  y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding='SAME')
  return y[0, :, :, 0]

def laplace(x):
  """Compute the 2D laplacian of an array """
  laplace_k = make_kernel([[0.5, 1.0, 0.5],
                           [1.0, -6., 1.0],
                           [0.5, 1.0, 0.5]])  
  return simple_conv(x, laplace_k)

# --- Define the PDE - the pond surface is a perfect 400x400 square
N = 400

# --- list of display points...
dispval = jump_range(0, 12500, 1000)
# --- dispval has to be a list...
dispval = list(dispval)
print "We will look at these values: ",dispval

# --- now, we create some "raindrops"
# --- Initial Conditions -- some rain drops hit the pond
# --- set everything to zero
u_init = np.zeros([N, N], dtype=np.float32)
ut_init = np.zeros([N, N], dtype=np.float32)

# Some material accretion occurs (raindrops hit pond) at random points
for n in range(40):
  a,b = np.random.randint(0, N, 2)
  u_init[a,b] = np.random.uniform()

# --- Create and Display the jpeg image...
# proc = subprocess.Popen(["display", "./tensor.jpg"])
# DisplayArray(u_init, rng=[-0.1, 0.1])

# Parameters
# eps -- time resolution
# damping -- wave damping
eps = tf.placeholder(tf.float32, shape=())
damping = tf.placeholder(tf.float32, shape=())

# --- Create vaiables for simulation state
U  = tf.Variable(u_init)
Ut = tf.Variable(u_init)

# --- Discretized PDE update rules
U_  = U + eps * Ut
Ut_ = Ut + eps * (laplace(U) - damping * Ut)

# --- Operation to update the state
step = tf.group(
  U.assign(U_),
  Ut.assign(Ut_))

# --- Run the simulation forward with a simple FOR loop.
# --- Initialize state to initial conditions
tf.global_variables_initializer().run(session=sess)

# --- Run 12701 steps of PDE
for i in range(12701):
  # Step simulation  (damping was 0.04, I made it negative .14)
   with sess.as_default(): step.run( {eps: 0.03, damping: -0.14})
# --- to see everything...
#   with sess.as_default(): print "U.eval()   .... ", U.eval()[20]  # --- ,"   ", Ut.eval()
# ------

   if (i in dispval) :
       with sess.as_default(): DisplayArray(U.eval(), rng=[-0.1, 0.1])
       print "                                ------ For iteration:  ",i
       sys.stdout.flush()
       print "U.eval()   ....... "
       with sess.as_default(): print   U.eval()[20]      # --- ,"   ", Ut.eval()
       print "                                --- End of iteration:  ",i
       sys.stdout.flush()
       continue
#
# --- to show each iteration...
#  with sess.as_default(): DisplayArray(U.eval(), rng=[-0.1, 0.1])
print "Done at: ",i

# --- Ok, we are done...
with sess.as_default(): DisplayArray(U.eval(), rng=[-0.1, 0.1])

with sess.as_default(): DisplayArrayToFile(U.eval(), rng=[-0.1, 0.1])
print "Last Image Written to file: tensor_new.jpg. Done."   
#--------------- done ------------------

If someone could try this program on a supported version of Linux (ie. the Ubuntu version that TensorFlow officially supports), that would be helpful. I am running a recent version of the Linux kernel on the CentOS-7.4 box (uname -a reports: kernel version 4.14.9-1.el7.elrepo.x86_64 ). Really like to nail down what is happening. I have attached images of results I am seeing on the two machines, first the Linux box, second is the Macbook.

[quaeler]

Installing from binary ( https://storage.googleapis.com/tensorflow/linux/cpu/tensorflow-1.4.1-cp27-none-linux_x86_64.whl ) on Ubuntu 17.10, Python 2.7.14, i also see the moire-style pattern evolution.

[Gemesys]

Thank you, quaeler, for posting your results. This is really useful. I was starting to think that there must be a problem in my Linux installation, because the MacOS version basically blows up to almost a white screen by interation 3000. I've been investigating various examples of 32-bit overflow bugs and problems in various Python packages, looking at anywhere TensorFlow or Python is producing different results on different platforms, and there are a few.

One that I found was a production server versus a development environment giving completely different results, which turned out to be a bug in a library called "bottleneck", used in the "pandas" data tool for Python. There is a Stackoverflow note on that issue: https://stackoverflow.com/questions/43525492/unexpected-32-bit-integer-overflow-in-pandas-numpy-int64-python-3-6?noredirect=1&lq=1

I am wondering if some of the speed-up code from "bottleneck" made it into TensorFlow, with the 32-bit overflow bug included, in one of the versions. Possible?

Here are the results of just the first three images, .ie the initial image (supposed to be stars), and the generated image at iteration 1000, and at iteration 2000, after which I interrupted the program. I changed the laplace damping value from a positive number in the TensorFlow example of "raindrops on a pond" to a negative value to simulate accretion... stars forming instead of raindrops falling.

You can see, the Macbook version evolves completely differently, with the generated values all going to positive numbers, while the Linux version evolves to what you are also seeing, a tensor of positive and negative values, which creates an interesting pattern. I basically have the same issue the fellow in the "integer-overflow-in-pandas-numpy" had, two machines with identical software and basically the same architecture that should behave the same, but clearly do not. Something is amiss.

I've checked that the defaults in the two Python's seem to be the same, all the packages are the same, and have just updated Pillow to 5.0.0 on both machines, with no change in observed behaviour. I will try to reduce this issue to a simple case where one of the machines is producing an obviously wrong result.

[cy89]

@Gemesys a simple reproduction case would be very useful. Please let us know what you find.

[quaeler]

Unfortunately, to add a problem to this problem, running this with Python 2.7.10 on macOS 10.12.6 and installing from https://storage.googleapis.com/tensorflow/mac/cpu/tensorflow-1.4.1-py2-none-any.whl produces the Linux-esque behavior.

[Gemesys]

Thank-you so much for this, quaeler! This is really helpful. The behaviour on your 10.12.6 macos matches exactly what I am seeing on my Linux box, which seems to be very stable, and does not show any evidence of any other issue anywhere, so far. I'm running Firefox 52.2 ESR, and a bunch of Tcl/Tk stuff, including an editor, some encryption stuff, and such. It all works, and I have confidence in the configuration. Your run Ubuntu was slightly different - but what you have provided here looks exactly like what I see, almost pixel-for-pixel. (I've attached proper screen-shot image from my Linux machine.) The simulation begins with pesudo-random values, but evolves always - despite changes in images size - to what you are showing here. I ran a 1200x1200 image sequence yesterday, and it still looked the same. I've downloaded and run some floating-point test/check software from here: http://www.math.utah.edu/~beebe/software/ieee/ and the screen-shot of running fpshow.c shows the repesentation of floating-point constants on the left for the Linux-CentOS-7.4 box and on the right for the MacBook, running 10.10.5 macos. (Centre is the info in the ieeeftn.h file, with explanations and indication of what is expected to be seen). In running different sizes of the output image, I notice that the behaviour matches between the two machines up to an image of about 90x90. Above that, the Mac blows up (image goes all white), ie. behaviour diverges.

Looks like a memory or overflow problem. The output of the "fpshow.c" program (provided below) shows that floating point representation between the Linux and Macbook are the same, for the 64-bit words. Linux side does show extranious data in next location, whereas Mac shows zeros, but that is an artifact of the fpshow.c program being written for 32-bit, I think. It's just showing next 64-bit memory location. The 64-bit numeric stuff is same on both, as far as I can tell. Both machines have 4 GB memory, for "gcc --version" Linux box reports: " 4.8.5 20150623 (Red Hat 4.8.5-16)", and the Mac reports: "Apple LLVM version 7.0.2 (clang-700.1.01) Target: x86_64-apple-darwin14.5.0, Thread model: posix".

I will try to make a more simple test case. But what you have provided here, suggests there is a bug in the Apple's macos (10.10.5 - Yosemite) memory management or floating-point calculation operation.

I also found an issue where a fellow reported bizarre training results for a network. Instead of a smooth curve of improvement (as the backprop progressed), he got these serious and strange discontiuous results - which yes, can happen if you are falling down a steep gradient in a new location on the error surface, but his results were curious - looked almost like a hardware failure, but then the training would recover. If there is a floating-point calculation issue, that only shows up in some cases, it might be the cause of this guy's strange training results. (Like the early 1995 Intel FPU bug. It was only apparent sometimes, for some calculations.)

But the fact that an upgraded version of the macos produces exactly the behaviour seen on my Linux box, suggests Apple's Yosemite is the culprit. I won't upgrade the Mac, as I would like to determine what is happening here. Results of the "fpshow.c" program (which "ieeeftn.h") from the above site (Univ. of Utah..), shown below. Linux and Mac floating-point representation seem the same, as one would expect. Also provide proper (not just Android-phone image..) screen shot from my Linux box, showing expected behaviour, same as what you are seeing on your macOS 10.12.6.

[Gemesys]

Given what quaeler reported, I uninstalled my built-from-source version of Tensorflow-1.4.1 on the Macbook, and installed the binary version of Tensorflow that quaeler used to get the correct simulation results he shows for Sierra macos. Then, I edited my .bash_profile to revert to the previous, binary installed Python (2.7.14), which has ucs2 encoding for unicode characters. (Thats the one issue I know is different between the Linux binary Tensorflow and the Mac binary Tensorflow. The Linux binary is built with unicode=ucs4, and requires a Python built the same way.)

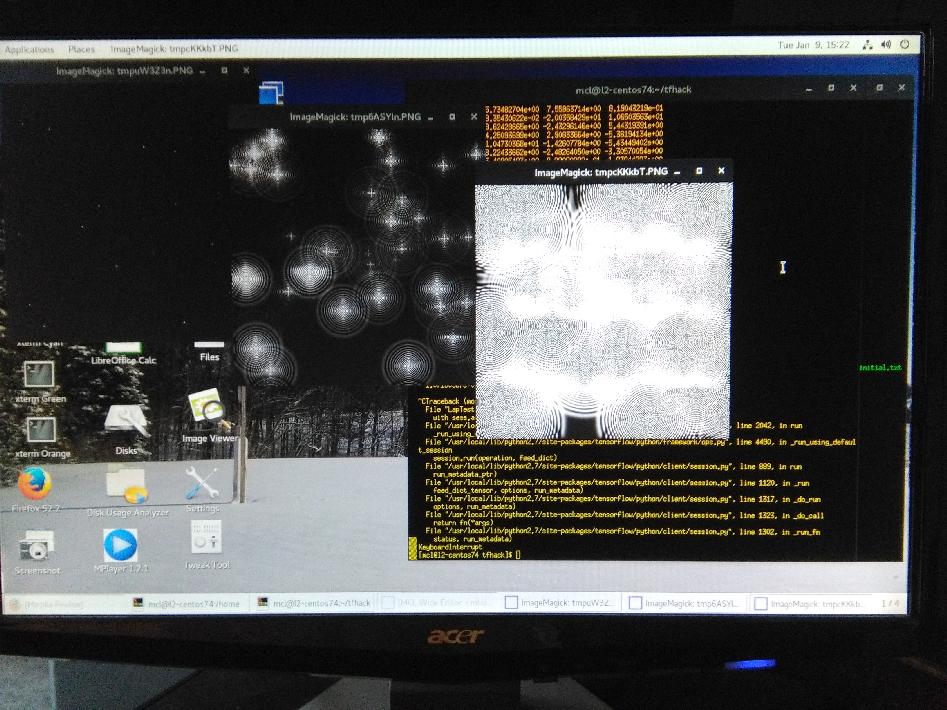
I ran the LapTest.py program on the Mac with binary Tensorflow and binary Python (2.7.14 from Sept. 2017), and confirmed I still get the blank image. I've attached a proper screenshot below, which shows the results - all blank white screens, after the simulation runs for just 3000 iterations. The floating point values in the U.eval() matrix (used to create the display image), for row=20 are provided in the xterm window, showing alll high-valued, positive values. On the Linux machine, these values are a mixture of postive and negative values (and hence an image is produced).

When run on Linux, the simulation evolves in the fashion quaeler reports for Mac Sierra, and I am seeing for Linux/CentOS-7.4. The numbers evolve the same way, and a similar image appears, even with a larger surface area, showing same evidence of moire-style patterns. The same inspection of the U.eval() matrix at row[20] shows high-valued positive and negative values, which are shown in the attached screenshot from the Linux box.

I thought it might be the CPU vectorization being problematic, but what is interesting is the Macbook compiled-from-source Tensorflow-1.4.1 does not offer the warning messages about cpu vector instructions sse4.1, sse4.2 and avx ("Your CPU has these, but this version is not compiled to use them: SSE4.1, SSE4.2 AVX"), but the binary version I just re-installed does offer this warning, so I am guessing that the ./configure and/or Bazel setup sees these CPU options are available, and compiles the code in Tensorflow to use these? So since the behaviour is the same on the Yosemite (10.10.15) Macbook for both compiled and binary Tensorflow, we can rule out the problem being from the use of the vector instructions? Or when you compile Tensorflow for CPU, do you have to explicitly set some options to use these instructions, and that assumption is not correct?

On each screen shot, the table at right is the U.eval() values for row[20]. The image display routine just uses np.clip to clamp the image-pixel values to between 0 and 255, so a large negative number becomes a zero (black), and a large positive number becomes a 255 (white).

To summarize: The Linux Tensorflow binary for 1.4.1 for both Ubuntu 17 and CentOS-7.4 have the simulation evolve to a big tensor of high-value positive and negative numbers, and pattern in the image is generated. The same numerical evolution occurs on a Macbook running Sierra Macos 10.12.6.

And now, what is particularly annoying, is that I cannot re-install my built-from-source version of TensorFlow-1.4.1, despite having pointed to and started the locally-built Python without problem. There is a wrapper file in the /usr/local/lib/python2.7/site-packages/tensorflow/python/_pywrap_tensorflow_internal.so which is failing on a "Symbol not found: _PyUnicodeUCS_AsASCIIString" Arrgh! What looks to have happened, is that installing the binay Tensorflow (with it's unicode=ucs2 default) has trashed the local-built Python 2.7 library. I have the ucs4 Python in the path, any attempt to import my local built TensorFlow in Python is failing. I will have to resolve this before I can determine what is wrong with the TensorFlow math under Yosemite.

[Gemesys]

In case anyone is following this, here is the protocol for switching back to your custom-built TF version, from a binary one. Just go to the directory where you built TF, and run ./configure to make sure you are pointing to your local python (I have a binary version installed in the ..frameworks area, and a local built one in /usr/local/bin with the site packages in /usr/local/lib/python2.7/site-packages/... ). Do a "bazel build", (runs real quick, nothing needs to be compiled...), and then run "bazel-bin/tensorflow/tools/pip_package/build_pip_package /tmp/tensorflow_pkg" and you will get the .whl file in ./tmp/tensorflow_pkg. Uninstall the binary TensorFlow in python with "pip uninstall tensorflow". Then change the name of the built .whl file if you need to (mine gets built as "tensorflow-1.4.1-cp27-cp27m-macosx_10_4_x86_64.whl, and I have to rename or copy it to: "tensorflow-1.4.1-py2-none-any.whl", and you can then use "pip install ... " to install it successfully. Start Python, and "import tensorflow as tf". This was failing for me, until it re-did the Bazel build. (Note: I am using Bazel 0.9.0, built from source.)

This gets me back to using my local-built TensorFlow and Python 2.7, with the unicode=ucs4 (same as the Linux binary Tensorflow and its local-built Python 2.7. ). Note, you can check which unicode level your Python is built with using : "import sys" and then "print sys.maxunicode". If you get "1114111", you are unicode=ucs4, if you get "65535", you are unicode=ucs2.

Once I rebuilt TensorFlow pointing to the right Python, and rebuilt the .whl file, and un-installed and then installed the new wheel file with pip install, I was again able to successfully import it, and run the test programs.

What is really curious, is that this switching between versions made absolutely no difference in the behaviour of the Macbook's version of the simulation test. On the Macbook with macos 10.10.5, the test floating-point values all go to large numbers, (and a pure white image) whereas on the other three platforms, the results oscillate between large positive and large negative numbers (and generate the moire-pattern image.). All processors are little-endian Intel multi-core devices, and their behaviour should not diverge this way. I've seen strange results like this before, and it was due to a serious flaw in a very low-level routine that converted between large floating-point values, and a 10-byte extended precision format that was rarely (but occasionally) used. Only when code used the 80-bit field, did the numbers go squirrelly - and when they did go off, it was only by a small amount. But the problem would show up on scientific graphs - the numbering on the axis would be "1 2 3 4 5 6 7 8 9 9" instead of "1 2 3 4 5 6 7 8 9 10". The situation here looks similar. Very large floating point numbers are being flipped between registers, pipelines, and/or memory, and somewhere, some are getting mis-converted or precision is being dropped incorrectly - or maybe added incorrectly?

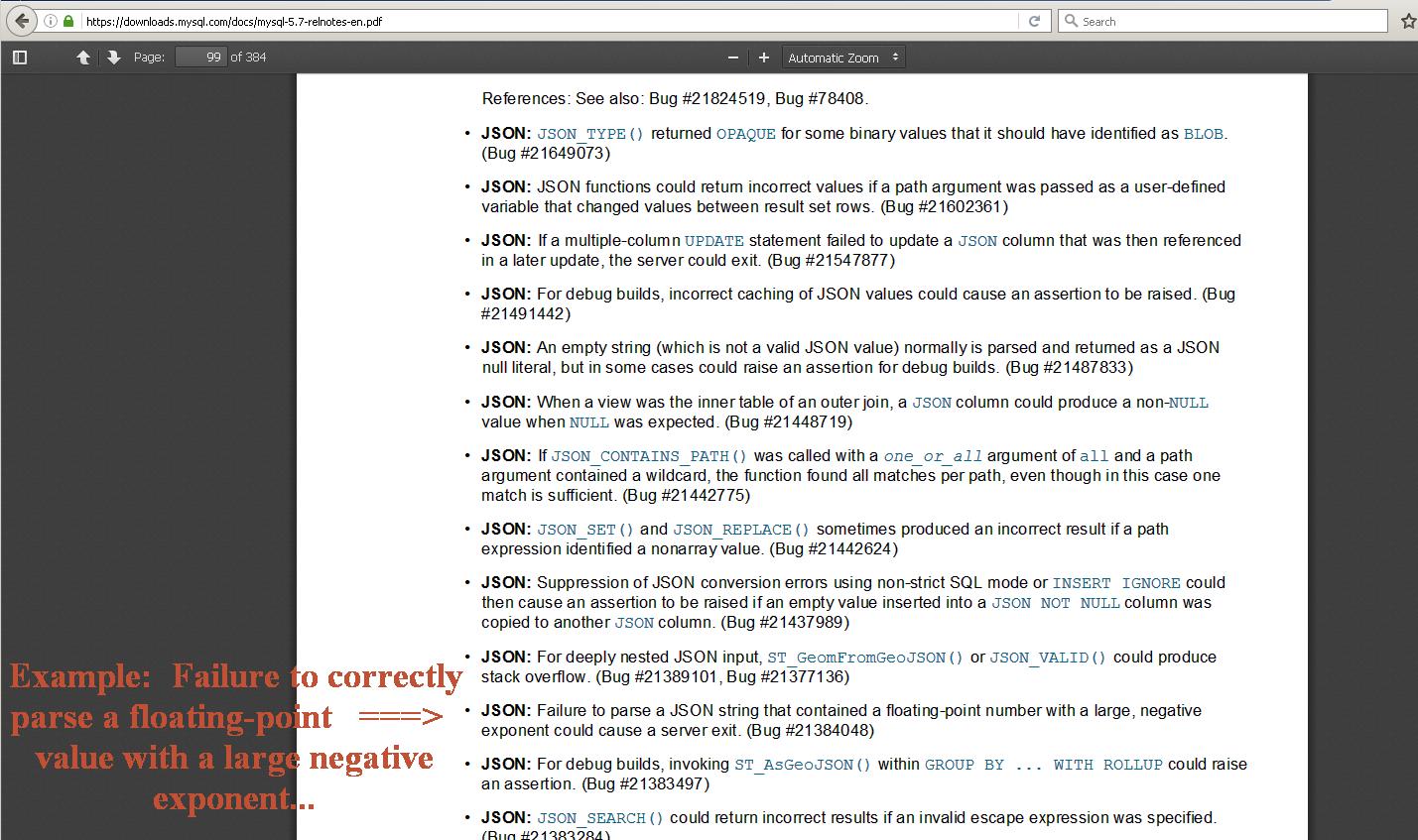
These type of errors are not uncommon. In the current MySql 5.7 release notes, deep on page 99 of an almost 400 page document, there is a reference to a JSON parsing error of a floating point number with a large negative exponent that apparently could crash the server. Image attached. Full document is at: https://downloads.mysql.com/docs/mysql-5.7-relnotes-en.pdf

As I said earlier, I will try to construct a more simple test-case that will illustrate the problem, but there is enough here that it might bear looking into by someone who knows the internals of TensorFlow. It is possible that the Macbook Yosemite operation is correct, and that the other three platforms are propagating erroneous results, perhaps due to flawed interprocessor communication or pipelining/prefetching errors. Until this evident calculation issue is understood, it is realistic to expect TensorFlow to give different training results on different machines of similar architecture, which is a real concern.

[Gemesys]

As promised, here is a more direct example of the operational difference noted between MacOS and Linux versions of TensorFlow 1.4.1. I've removed all randomness from the initial conditions of the test program, and removed the need to use scipy, PIL/Pillow and matplotlib (and the TkAgg backend). All we are basically doing here his calling TensorFlow routines: "tf.expand_dims" and "tf.nn.depthwise_conv2d" to set things up, "tf.group" to define the step, "tf.global_variables_initializer" to initialize variables, and "step.run" to iterate.

Row 20 of the matrix "U" is displayed using U.eval. This prints 400 numbers. After only 1000 iterations, the Linux version of TensorFlow 1.4.1 shows the first number in row 20 of U as a value that is typically around 1.4 to 1.5. The MacOS version (running on MacOS 10.10.5 (Yosemite)), typically shows a value around 0.336 to 0.337. One can simply interupt the running Python program with control-c, and examine the 400 numbers displayed for iteration 1000, when the program displays the iteration=1000 information.

These differences remain essentially the same, with small floating-point numeric variations between runs, the source of which is unclear at this time. Each machine shows small variations in its results each time, after only 1000 iterations (a few percentage points different). This may be due to characteristic operation of the floating-point solid-state electronics. But between platforms, the difference exceeds 300 percent, and this has to be seen as unacceptable. From run to run, this magnitude of difference remains consistant. So far, I have been unable to detect any specifc flaw in floating point operations on the Macbook Pro running under MacOS 10.10.5, nor on the HP box, which is running under CentOS Linux 7.4.

TensorFlow is producing quite different results on two different (but architecturally similar) computers.

The test program, "laptestnum.py" is attached below.

#-------------------------------------------------------------------------------
# Prgm: laptestnum.py
#
# --- all randomness at startup is removed.  Program begins with specified
# --- input values that are exactly the same for each run.
#
# --- this is a stripped-down version of LapTest.py, just produces numbers,
# --- and a final image to "tensor_new.jpg".  Does not require scipy.misc
# --- does not require PIL/Pillow image processing library
# --- does not use or require matplotlib or TkAgg backend
# --- does not produce images while running - only outputs row 20 of matrix U.eval()
# --- 
# --- one may interrupt program with ctrl-c after only 1000 iterations, and
# --- note the dramatic difference between the Apple Mac (10.10.5 MacOS) and
# --- Linux version.  
#
# --- the Tensorflow LaPlace Image example (Uses PIL(Pillow ver.), and numpy)
# --- updated for TensorFlow 1.4.0 running on CentOS-7.4 & Python 2.7.14
#     compiled (configured, actually) with the "--enable-unicode=ucs4" option
#                                             (Python compile default is ucs2)
#                                             (which caused TensorFlow 1.4 to)
#                                             (fail to load. Building Python )
#                                             (with ucs4, => pip can install )
#                                             (TensorFlow 1.4.0 successfully.)

# --- Import various libraries for simulation
import tensorflow as tf
import numpy as np
# import scipy.misc
import imageio
# import os
import sys
import subprocess
# import PIL
# import time    

# --- Import for visualization and jpeg encoder  
# import matplotlib
# matplotlib.rcParams["backend"]= 'TkAgg'
# from matplotlib import pyplot as plt
# from PIL import Image, ImageDraw
from io import BytesIO
#  from IPython.display import clear_output, Image, display

#--- we need this to get a sane for-loop...
def jump_range(start, end, step):
    while start <= end:
        yield start
        start += step

# --- function for displaying state of the pond's surface as an image
def DisplayArray(a, fmt='jpeg', rng=[0,1]):
  global proc
  # proc.kill() 
  # """Display an array as a picture. """
  a = (a - float(rng[0]))/float(rng[1] - rng[0])*37
  amod = np.clip(a, 0, 255)
  a = np.uint8(amod)
#  a = np.clip(a, 0, 255) 
#  a = np.uint8(a) 
#  np.clip(a, 0, 255, out=a )
#  a = a.astype('uint8')
  print " "
  print " ----------- This is a: => row 20  ------------"
  print a[20]
  print " ----------------------------------------------"
  f = BytesIO()
  # --- this is the cool, realtime thing that runs in Jupyter-IPython Notebook
  # PIL.Image.fromarray(a).save(f,fmt)
  # --- clear_output(wait = True)  --- only for IPython
  # display(Image(data=f.getvalue()))
  # --- write the image
  # --- write the simulation images to .jpg files
  # scipy.misc.imsave("tensor.jpg", a)
  # pic = PIL.Image.open("tensor.jpg")
  # --- new approach... use subprocess, wait for time(2) then kill it
  # proc = subprocess.Popen(["display", "./tensor.jpg"])
  # time.sleep(0.5)
  # pic.show()
  # clear_output(wait=True)
  # --- this line below doesn't work outside of the Jupyter environment...
  # display(Image(data=f.getvalue()))
  #
  # pic.close()  <--- does not work to close image.  Just removes the pointer to image in memory

def DisplayArrayToFile(a, fmt='jpeg', rng=[0,1]):
  # """Display an array as a picture to a file... """
  a = (a - float(rng[0]))/float(rng[1] - rng[0])*37
  a = np.uint8(np.clip(a, 0, 255))
  f = BytesIO()
  # --- this is the cool, realtime thing that runs in Jupyter-IPython Notebook
  # PIL.Image.fromarray(a).save(f,fmt)
  # clear_output(wait = True)
  # display(Image(data=f.getvalue()))
  # --- write the image
  # --- this is my stuff to write the simulation images to .jpg files
  #scipy.misc.imsave ("tensor_new.jpg", a)
  imageio.imwrite("tensor_new.jpg", a)
  # --- image = PIL.Image.open("tensor_new.jpg")
  # --- image.show()
  # clear_output(wait=True)
  # display(Image(data=f.getvalue()))
  #

# --- make print stmt print the whole array... (not just part of it...)
np.set_printoptions(threshold=np.nan)

# --- make interactive session for testing - can use regular session also
sess = tf.InteractiveSession()
# sess = tf.Session()

# --- computational functions go here... once we get jpeg pic working
def make_kernel(a):
  """Transform a 2D array into a convolutional kernel """  
  a = np.asarray(a, dtype=np.float32)
  a = a.reshape(list(a.shape) + [1,1])
  return tf.constant(a, dtype=1)

def simple_conv(x, k):
  """ A simplified 2D convolutional operation """
  x = tf.expand_dims(tf.expand_dims(x, 0), -1)
  print "simple_conv x dtype is: ", x.dtype
  print " x is ....:", x
  print "simple_conv k dtype is: ", k.dtype
  print " k is ....:", k
  y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding='SAME')
  print "simple_conv y dtype is: ", y.dtype
  print " y is ....", y
  return y[0, :, :, 0]

def laplace(x):
  """Compute the 2D laplacian of an array """
  laplace_k = make_kernel([[0.5, 1.0, 0.5],
                           [1.0, -6., 1.0],
                           [0.5, 1.0, 0.5]])  
  return simple_conv(x, laplace_k)

# --- Define the PDE - the pond surface is a perfect 400x400 square
print "\nLaplace PDE Simulation Test \n"
N = 400
print "Surface square side is: ",N

# --- list of display points...
dispval = jump_range(0, 12500, 1000)
# --- dispval has to be a list...
dispval = list(dispval)
print "We will look at these values: ",dispval

# --- now, we create some "raindrops"
# --- Initial Conditions -- some rain drops hit the pond
# --- set everything to zero
u_init = np.zeros([N, N], dtype=np.float32)
ut_init = np.zeros([N, N], dtype=np.float32)

# Some material accretion occurs (raindrops hit pond) at random points
# for n in range(40):
#   a,b = np.random.randint(0, N, 2)
#   u_init[a,b] = np.random.uniform()

# --- not random.  Fixed & same each run
u_init[10,20]   = 1.4565
u_init[12,100]  = 0.7522
u_init[112,37]  = 1.21223
u_init[230,139] = 0.9756
u_init[301,205] = 1.7899
u_init[372,347] = 0.4588
u_init[74,193]  = 0.11987
u_init[89,312]  = 1.1877
u_init[178,287] = 1.5744
u_init[197,276] = 0.9876

u_init[101,21]  = 0.4565
u_init[132,290] = 1.2522
u_init[212,207] = 1.41223
u_init[130,139] = 1.5672
u_init[201,115] = 0.7899
u_init[162,307] = 1.4588
u_init[274,163] = 1.9187
u_init[189,212] = 0.1877
u_init[278,187] = 1.3744
u_init[156,76]  = 1.9876

# --- Create and Display the jpeg image...
# proc = subprocess.Popen(["display", "./tensor.jpg"])
# DisplayArray(u_init, rng=[-0.1, 0.1])

# Parameters
# eps -- time resolution
# damping -- wave damping
eps = tf.placeholder(tf.float32, shape=())
damping = tf.placeholder(tf.float32, shape=())

# --- Create vaiables for simulation state
U  = tf.Variable(u_init)
Ut = tf.Variable(u_init)

# --- Discretized PDE update rules
U_  = U + eps * Ut
Ut_ = Ut + eps * (laplace(U) - damping * Ut)

# --- Operation to update the state
step = tf.group(
  U.assign(U_),
  Ut.assign(Ut_))

# --- Run the simulation forward with a simple FOR loop.
# --- Initialize state to initial conditions
tf.global_variables_initializer().run(session=sess)

# --- Run 12701 steps of PDE
for i in range(12701):
  # Step simulation  (damping was 0.04, I made it negative .14)
   with sess.as_default(): step.run( {eps: 0.03, damping: -0.14})
# --- to see everything...
#   with sess.as_default(): print "U.eval()   .... ", U.eval()[20]  # --- ,"   ", Ut.eval()
# ------

   if (i in dispval) :
       print "                                ------ Showing iteration:  ",i
       sys.stdout.flush()
       with sess.as_default(): DisplayArray(U.eval(), rng=[-0.1, 0.1])
       print "                                ------ Within  iteration:  ",i
       sys.stdout.flush()
       print "U.eval()[20]   ....... "
       with sess.as_default(): print   U.eval()[20]      # --- ,"   ", Ut.eval()
       print "                                ------- End of iteration:  ",i
       sys.stdout.flush()
       continue
#
# --- to show each iteration...
#  with sess.as_default(): DisplayArray(U.eval(), rng=[-0.1, 0.1])
print "Done at: ",i

# --- Ok, we are done...
with sess.as_default(): DisplayArray(U.eval(), rng=[-0.1, 0.1])
print "U.eval()[20]   ....... "
with sess.as_default(): print   U.eval()[20]      # --- ,"   ", Ut.eval()
print "Done. ---  Square side size was: ",N

with sess.as_default(): DisplayArrayToFile(U.eval(), rng=[-0.1, 0.1])
print "Last Image Written to file: tensor_new.jpg. Done."   
#--------------- done ------------------

[quaeler]

Continued nice work - thank you so much.

Can confirm on my 10.12.6 macOS install:

                                ------ Within  iteration:   1000
U.eval()[20]   ....... 
[ 1.55104232e+00  1.91745281e-01 -1.13406909e+00  6.31072104e-01
  1.93640149e+00 -3.73377651e-01 -1.74114001e+00  6.54113710e-01
  1.28882718e+00 -1.54986036e+00 -1.63447249e+00  1.18530083e+00
...

( @cy89 )

[Gemesys]

Thanx quaeler, for the 10.12.6 macOS results. Your numbers are similar, but not exactly same as on my CentOS-7.4 HP box. (The signs are the same, numbers a little different, maybe 5% variance.) Looks like something curious with Macbook Pro, Core-i5 maybe, since it goes so far different so early.

I've found the Univ. of Calif. Berkeley (UCB) floating-point test suite by W. Kahan, circa 1989-1992. It is a whole bunch of Fortran-77 programs that check and verify floating-point math, at various levels of precision. Before I open up TensorFlow in any detail, I figured I better do this kind of check. The programs use CPP (the C pre-processor), => great bunches of #defines for different levels of precision (real 4, real 8 and even real *16 (quad precision, I guess...)). The Makefile's won't run, but I think I can get some of the key test programs running. This stuff was mostly written for DEC Vax and Sun Workstations, & parts of it retain aggressive copyright notices - but it has been published, so I am going to use it.

I have "gfortran" on both CentOS and MacOS, (downloaded gfortran 5.2 as a .dmg for the Mac), so I should be able to convert and compile at least some of the programs, and see what differences I can find. It looks like the error occurs when exponents get big, ie. over 30 or 40.

Once I get some of the stuff running, I will post results - tonite or tomorrow. - Mark.

On 1/17/18, loki der quaeler notifications@github.com wrote:

Continued nice work - thank you so much.

Can confirm on my 10.12.6 macOS install:

                                ------ Within  iteration:   1000
U.eval()[20]   .......
[ 1.55104232e+00  1.91745281e-01 -1.13406909e+00  6.31072104e-01
  1.93640149e+00 -3.73377651e-01 -1.74114001e+00  6.54113710e-01
  1.28882718e+00 -1.54986036e+00 -1.63447249e+00  1.18530083e+00
...

-- You are receiving this because you were mentioned. Reply to this email directly or view it on GitHub: https://github.com/tensorflow/tensorflow/issues/15933#issuecomment-358468608

[Gemesys]

Attached is part of a test suite from Univ. of California Berkeley, which was used to test and verify floating point operations on several machines, from DEC VAX and Sun Microsystems machines to early P/C's. It was originally written for Fortran77. I've converted the "pi.F" program (to "pi_new.F") to compile and run in gFortran (GNU Fortran), in DP (double-precision) mode. What I am seeing, is that the MacOS and CentOS-7.4 Linux produce exactly the same results, up to where the remainder value reaches floating point values where the exponent is near or slightly above 25. (see the attached single screenshot, which shows the MacOS result on the left, the CentOS-7.4 result on the right.)

i downloaded and installed "gfortran" binary for MacOS (the version 5.2 for Yosemite), and gfortran 4.8.5 (and gcc 4.8.5) are installed with CentOS-7.4. On the Macbook, I installed macOS gfortran ver. 5.2 (for 10.10 Yosemite), as a .dmg binary. Fortran binaries for MacOS available here: https://gcc.gnu.org/wiki/GFortranBinaries

The "pi_new.F" program can be compiled with the following command line:

gfortran -cpp -D DP  pi_new.F -o  pi_new

The program calculates pi using progressively larger operands, and reports the results. It also makes 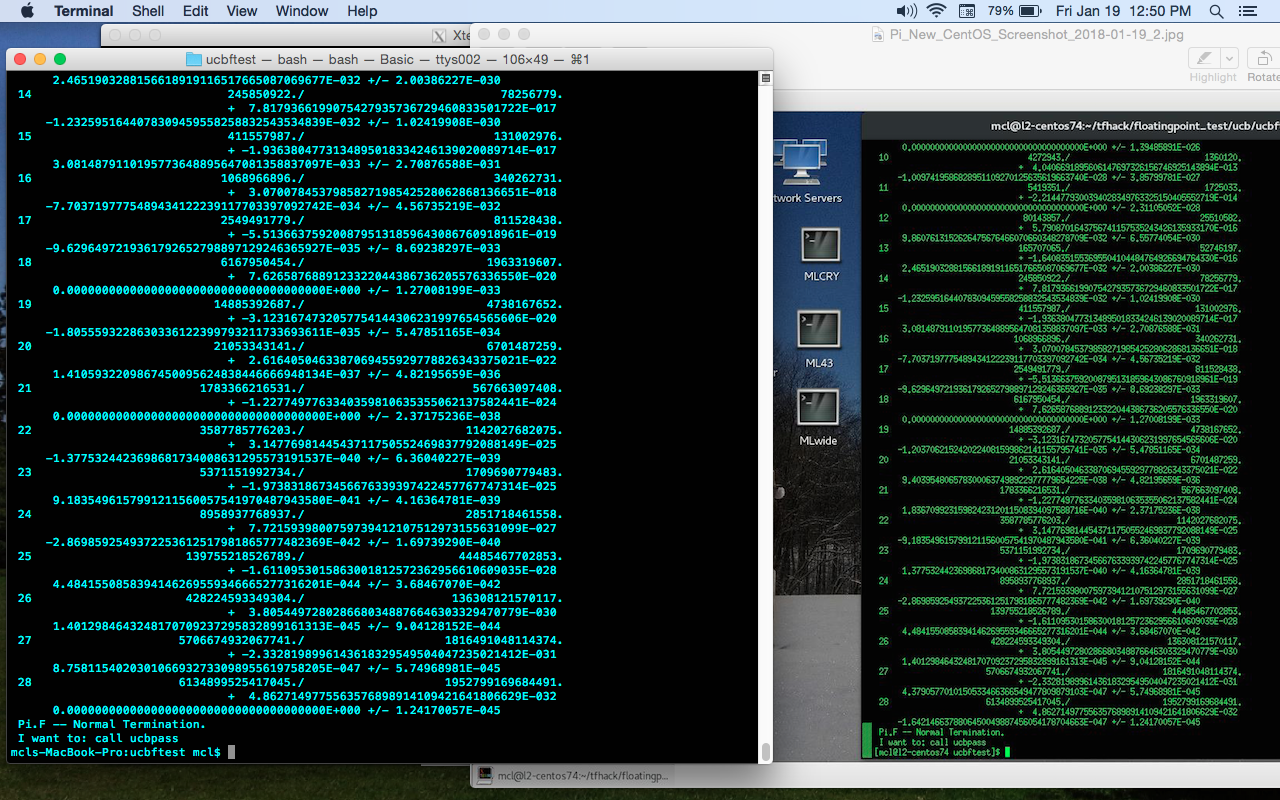tests for internal consistancy, which both platforms pass. At iteration 8, the remainders are different. And at iterations 19 to 24 show serious divergence in the remainder values. The remainder on iteration 23 on the Macbook, is the value for the the remainder for iteration 22 on the CentOS box, but with the sign flipped. The remainder for iteration 22 on the Macbook (-1.37753244... E-40), is the value for the remainder for iteration 23 on the CentOS box, but again, with the sign flipped to positive. But by iterations 24, 25 and 26, the results are exactly the same, only to diverge again for iterations 27 and 28. To me, this seems to indicate a rather serious issue, which appears to be independent of TensorFlow. The MacBook is giving different results than the 64-bit Linux box.

So far, I just have this one program converted, but I will try to convert the entire test suite, and run it to see if the MacOS - Linux 64-bit floating-point calculations divergence shows up in other calculations. The "pi_new.F" program source is below...

C "@(#)pirats.F 1.2 92/05/29 SMI"

#define STDERR 0
#define STDOUT 6
#define STDIN 5
#ifdef SP
#define REAL real*4
#define EXPO e0
#endif
#ifdef DP
#define REAL real*8
#define EXPO d0
#endif
#ifdef QP
#define REAL real*16
#define EXPO q0
#endif

#ifdef TRIGP
#define SIN sinp
#define COS cosp
#define TAN tanp
#define ASIN asinp
#define ACOS acosp
#define ATAN atanp
#else
#define SIN sin
#define COS cos
#define TAN tan
#define ASIN asin
#define ACOS acos
#define ATAN atan
#endif

      PROGRAM PIRATS
C
C.... PIRATS                     Copyright (C) by W. Kahan, Mar. 8, 1989
C
C.... This program finds close rational approximations
C.... A/B to PI, and computes the differences C = PI-A/B to
C.... working precision within errors no bigger than E.  Working
C.... precision arithmetic is presumed to carry no more than about
C.... 110 sig. dec., and to be rounded reasonably like a DEC VAX
C.... or an HP calculator or in conformity with IEEE 754/854.
C.... Then the program tests argument reductions in functions SIN,
C.... COS and TAN, checking to see whether they are consistent
C.... with the hypothesis that their actual periods are some single
C.... close approximation 2*P to 2*PI if not 2*PI itself.
C
      INTEGER NPI
      PARAMETER (NPI = 210)
C
C.... The following array of NPI+1 divisors D(J) > 0 in the continued
C.... fraction PI = D(0)+1/(D(1)+1/(D(2)+1/(D(3)+...))) will incur an
C.... error in PI no worse than 3.6E-234. Only D(NPI) isn't an integer.
C.... This data is based upon DJ's computed by Stewart McDonald
C.... in 1983 from an algorithm due to W. Gosper.  W. K.
C
      INTEGER I,J,INC
      REAL D(0:NPI),EPS,RDX,FL,A,B,C,E,R
      DATA (D(I),I = 0,99)/
     1   3. EXPO ,7. EXPO ,15. EXPO ,1. EXPO ,292. EXPO ,1. EXPO ,
     1  1. EXPO ,1. EXPO ,2. EXPO ,1. EXPO ,
     2   3. EXPO ,1. EXPO ,14. EXPO ,2. EXPO ,1. EXPO ,1. EXPO ,
     1  2. EXPO ,2. EXPO ,2. EXPO ,2. EXPO ,
     3   1. EXPO ,84. EXPO ,2. EXPO ,1. EXPO ,1. EXPO ,15. EXPO ,
     1  3. EXPO ,13. EXPO ,1. EXPO ,4. EXPO ,
     4   2. EXPO ,6. EXPO ,6. EXPO ,99. EXPO ,1. EXPO ,2. EXPO ,
     1  2. EXPO ,6. EXPO ,3. EXPO ,5. EXPO ,
     5   1. EXPO ,1. EXPO ,6. EXPO ,8. EXPO ,1. EXPO ,7. EXPO ,1. EXPO,
     1  2. EXPO ,3. EXPO ,7. EXPO ,
     6   1. EXPO ,2. EXPO ,1. EXPO ,1. EXPO ,12. EXPO ,1. EXPO ,
     1  1. EXPO ,1. EXPO ,3. EXPO ,1. EXPO ,
     7   1. EXPO ,8. EXPO ,1. EXPO ,1. EXPO ,2. EXPO ,1. EXPO ,6. EXPO,
     1  1. EXPO ,1. EXPO ,5. EXPO ,
     8   2. EXPO ,2. EXPO ,3. EXPO ,1. EXPO ,2. EXPO ,4. EXPO ,4. EXPO,
     1  16. EXPO ,1. EXPO ,161. EXPO , 45. EXPO ,1. EXPO ,22. EXPO ,
     1  1. EXPO ,2. EXPO ,2. EXPO,1. EXPO,4. EXPO ,1. EXPO ,2. EXPO ,
     2  24. EXPO ,1. EXPO ,2. EXPO ,1. EXPO ,3. EXPO ,1. EXPO ,2. EXPO, 
     1  1. EXPO ,1. EXPO ,10. EXPO /

      DATA (D(I),I = 100,199)/
     1   2. EXPO ,5. EXPO ,4. EXPO ,1. EXPO ,2. EXPO ,2. EXPO ,8. EXPO ,
     1  1. EXPO ,5. EXPO ,2. EXPO ,
     2   2. EXPO ,26. EXPO ,1. EXPO ,4. EXPO ,1. EXPO ,1. EXPO ,8. EXPO 
     1  ,2. EXPO ,42. EXPO ,2. EXPO ,
     3   1. EXPO ,7. EXPO ,3. EXPO ,3. EXPO ,1. EXPO ,1. EXPO ,7. EXPO ,
     1  2. EXPO ,4. EXPO ,9. EXPO ,
     4   7. EXPO ,2. EXPO ,3. EXPO ,1. EXPO ,57. EXPO ,1. EXPO ,18. EXPO
     1   ,1. EXPO ,9. EXPO ,19. EXPO ,
     5   1. EXPO ,2. EXPO ,18. EXPO ,1. EXPO ,3. EXPO ,7. EXPO ,30. EXPO
     1   ,1. EXPO ,1. EXPO ,1. EXPO ,
     6   3. EXPO ,3. EXPO ,3. EXPO ,1. EXPO ,2. EXPO ,8. EXPO ,1. EXPO ,
     1  1. EXPO ,2. EXPO ,1. EXPO ,
     7   15. EXPO ,1. EXPO ,2. EXPO ,13. EXPO ,1. EXPO ,2. EXPO ,1. EXPO
     1   ,4. EXPO ,1. EXPO ,12. EXPO ,
     8   1. EXPO ,1. EXPO ,3. EXPO ,3. EXPO ,28. EXPO ,1. EXPO ,10. EXPO
     1   ,3. EXPO ,2. EXPO ,20. EXPO ,
     9   1. EXPO ,1. EXPO ,1. EXPO ,1. EXPO ,4. EXPO ,1. EXPO ,1. EXPO ,
     1  1. EXPO ,5. EXPO ,3. EXPO , 2. EXPO ,1. EXPO ,6. EXPO ,1. EXPO ,
     1  4. EXPO ,1. EXPO ,120. EXPO ,2. EXPO ,1. EXPO ,1. EXPO /
      DATA (D(I),I = 200,NPI)/
     1   3. EXPO ,1. EXPO ,23. EXPO ,1. EXPO ,15. EXPO ,1. EXPO ,3. EXPO
     1   ,7. EXPO ,1. EXPO ,16. EXPO ,
     2   1.338371961073448 EXPO 
     3   /
C
C.... Environmental constants EPS, RDX, FL
C
      CALL ENVCNS(EPS,RDX,FL)
C
C.... for adequate accuracy
C
      INC = INT(LOG(FL)/LOG(2.6 EXPO ))
C
      PRINT 1000
1000  FORMAT(1X,'PIRATS: computes  PI = A/B+C and R = PI-P.'/
     1   /1X,1X,'J',1X,18X,'A',18X,'/',18X,'B'
     2   /1X,2X,1X,27X,'+',5X,'C'
     3   /1X,2X,1X,41X,'R',5X,'+/-',5X,'E'
     4   )
C
C.... Initialize A, B
C
      A = D(0)
      B = 1. EXPO 
C
      DO 100 J = 1,NPI-INC+5
C
C.... Get next pair A, B
C
         CALL NEXTAB(D(J),A,B)
         IF (A.GT.FL.OR.B.GT.FL) THEN
        GOTO 110
     ENDIF
C
C....    Get C = PI-A/B+/-E
C
         CALL GETCE(NPI,J,INC,EPS,FL,D,C,E)
C
C....    Get R = PI-P+/-E
C
         CALL TSTRIG(EPS,A,B,C,E,R)
C
C....    Display these numbers
C
         CALL DISPLA(J,A,B,C,E,R)
C
C....    Test them for consistency
C
         CALL COMPAR(E,R)
100   CONTINUE
110   CONTINUE
C
C.... Normal termination.
C
      PRINT *,'Pi.F -- Normal Termination. '
      PRINT *,'I want to: call ucbpass'
C      call ucbpass
      STOP
      END
C
    REAL function volatilizer(x)
    REAL x
    volatilizer=x
    end

      SUBROUTINE ENVCNS(EPS,RDX,FL)
      REAL EPS,RDX,FL
C
C.... Environmental constants.  This subroutine computes
C....    EPS = nextafter(1,2)-1 = 1.000...001-1
C....    RDX = RaDiX of floating-point arithmetic (2, 10, 16)
C....    FL = RDX/EPS = last of consecutive floating-point integers
C....                       among 1, 2, 3, ..., FL-2, FL-1, FL.
C
C.... local variables
C
    REAL volatilizer
      REAL H,X,Y,T,U,V
C
C.... First seek EPS
C
      T = 4. EXPO /3. EXPO 
      X = T-1. EXPO 
      Y = ABS((X+X-1. EXPO )+X)/64. EXPO 
      EPS = 0. EXPO 
      IF (Y.EQ.0. EXPO ) THEN
     PRINT *,'Is 4/3 exact?'
         GOTO 299
      ENDIF
200   IF (EPS.NE.0. EXPO ) GOTO 210
         U = volatilizer(1. EXPO +Y)
         EPS = volatilizer(U-1. EXPO) 
         Y = Y+Y
      GOTO 200
C
C     Now seek EPS/RDX = 1-nextafter(1,0) = 1-0.999...999 :
C
210   H = 1. EXPO /2. EXPO 
      T = 2. EXPO /3. EXPO 
      X = T-H
      Y = ABS((X+X-H)+X)/64. EXPO 
      V = 0. EXPO 
      IF (Y.EQ.0. EXPO ) THEN
     PRINT *,'Is 2/3 exact?'
         GOTO 299
      ENDIF
220   IF (V.NE.0. EXPO ) GOTO 230
         U = volatilizer((H-Y)+H)
         V = volatilizer((H-U)+H)
         Y = Y+Y
      GOTO 220
C
C.... in case Division is dirty
C
230   RDX = AINT(EPS/V+0.0001 EXPO )
      IF (RDX.LT.2. EXPO ) THEN
     PRINT 5000,'Radix =',RDX
5000     FORMAT(1X,A,F4.0)
         GOTO 299
      ENDIF
C
C.... Confirm that RDX = Radix of Floating-point arithmetic.
C
      T = RDX
      X = 1. EXPO 
C
C.... until X.EQ.0 or X.EQ.RDX
C
240   IF (X.NE.1. EXPO ) GOTO 250
         T = T+T
         U = volatilizer(T+1. EXPO)
         X = volatilizer(U-T)
      GOTO 240
250   IF (X.EQ.0. EXPO ) THEN
         Y = 1. EXPO 
260      IF (X.NE.0. EXPO ) GOTO 270
            Y = Y+Y
            U = volatilizer(T+Y)
            X = volatilizer(U-T)
     GOTO 260
      ENDIF
270   IF (X.NE.RDX) THEN
         PRINT 6000,'Is Radix ',X,' or ',RDX,'?'
6000     FORMAT(1X,A,F4.0,A,F4.0,A)
     GOTO 299
      ENDIF
C
C.... Confirm that FL = RDX/EPS:
C
      FL = RDX
      X = 1. EXPO 
280   IF (X.NE.1. EXPO ) GOTO 290
         FL = volatilizer(FL*RDX)
     U = volatilizer(FL+1. EXPO)
     X = volatilizer(U-FL)
      GOTO 280
290   IF (FL*V.EQ.1. EXPO ) THEN
     RETURN
      ENDIF
C
C.... ENVCNS cannot compute environmental constants correctly:
C
      PRINT 3000,'Is FL ',FL,' or ',1. EXPO /V,'?'
3000  FORMAT(1X,A6,1PE45.37E3/1X,2X,A4,1PE45.37E3,A1)
299   PRINT *,'Subroutine ENVCNS cannot compute correctly the'
      PRINT *,'Environmental constants'
      PRINT *,'EPS = 1.000...001 - 1 , and'
      PRINT *,'FL = Last consecutive Floating-point integer'
      PRINT *,'        among 1, 2, 3, ..., FL-2, FL-1, FL.'
      PRINT *,'Please substitute them for the subroutine.'
      PRINT *,'I want to: call ucbfail'
C   call ucbfail
      STOP
      END
C
      SUBROUTINE NEXTAB(DJ,A,B)
      REAL DJ,A,B
C
C.... Get next pair A, B
C
C.... local variables
C
      REAL T,A0,B0
      SAVE A0,B0
      DATA A0,B0/1. EXPO ,0. EXPO /
C
      T = DJ*B+B0
      B0 = B
      B = T
      T = DJ*A+A0
      A0 = A
      A = T
C
C.... Now A/B = D0+1/(D1+1/(D2+...+1/DJ)).
C
      RETURN
      END
C
      SUBROUTINE GETCE(NPI,J,INC,EPS,FL,D,C,E)
      INTEGER NPI,J,INC
      REAL EPS,FL,D(0:NPI),C,E
C
C.... This subroutine computes the continued fraction's tail
C....    Z = D(J+1)+1/(D(J+2)+1/(D(J+3)+1/(D(J+4)+...)))
C.... to working accuracy by using INC terms of it, and then
C.... computes the effect C of cutting it off to get A/B .
C....
C.... Get  C = PI-A/B+/-E
C
C.... local variables
C
      INTEGER I,I9
      REAL X,Y,Z
C
      I9 = MIN(NPI,J+INC)
      Z = D(I9)
      DO 400 I = I9-1,J+1,-1
         Z = D(I)+1. EXPO /Z
400   CONTINUE
      X = FL*FL
C
C.... C = 1/Z-1/X always
C
      C = 1. EXPO /Z-1. EXPO /X
      DO 410 I = J,1,-1
     Y = D(I)
         Z = Y+1. EXPO /Z
     X = Y+1. EXPO /X
     C = -C/(X*Z)
410   CONTINUE
C
C.... E > accumulated roundoff (mixed arithmetic)
C
      E = 4. EXPO *J*EPS*ABS(C)
      RETURN
      END
C
      SUBROUTINE TSTRIG(EPS,A,B,C,E,R)
      REAL EPS,A,B,C,E,R
C
C.... Get R = PI-P+/-E
C
C     This subroutine tests whether the programs that compute
C     TRIG(X) = trig(X*PI/P) for TRIG = SIN, COS or TAN
C     always use the same approximation P to PI during their
C     argument reduction.  If so, 3 or 4 values R = Q+C
C     derived from A = B*(PI-C+/-E) ought to agree.
C
C.... local variables
C
      REAL Q,Q0,S,W,W0,X,Y
      CHARACTER*11 TS
C
      REAL FNODD
      CHARACTER FNS
C
      CHARACTER*10 SI,CO,TA
      DATA SI,CO,TA/'arcsin(sin','arcsin(cos','arctan(tan'/
C
C.... FNODD(floating-point integer X) = (-1)**X
C
      FNODD(X) = (AINT(ABS(X)*0.5 EXPO +0.125 EXPO )*2. EXPO -ABS(X))*
     1  2. EXPO +1. EXPO 
C
C.... FNS(1) = '+', FNS(-1) = '-'
C
      FNS(X) = CHAR(44-INT(X))
C
      Q = ATAN(TAN(A))/B
      R = Q+C
      W = 3. EXPO *EPS*ABS(Q)
      E = E+W
      S = FNODD(B)
      X = A
      Y = B
      TS = FNS(S)//SI
      Q0 = ASIN(SIN(X))/Y*S
      W0 = W+6. EXPO *EPS*ABS(Q0)
      CALL WHET(Q,Q0,W0,X,Y,A,B,TS,TA)
      X = A*0.5 EXPO 
      Y = B*0.5 EXPO 
      IF (S.LT.0. EXPO ) THEN
C
C....    (B+1) is even
C
         S = FNODD((B+1. EXPO )*0.5 EXPO )
         TS = FNS(S)//CO
         Q0 = ASIN(COS(X))/Y*S
         W0 = W+6. EXPO *EPS*ABS(Q0)
      ELSE
C
C....    B = 2y is even
C
         TS = ' '//TA
         Q0 = ATAN(TAN(X))/Y
         W0 = 3. EXPO *EPS*ABS(Q0)
     CALL WHET(Q,Q0,W0,X,Y,A,B,TS,TA)
         S = FNODD(Y)
         TS = FNS(S)//SI
     Q0 = ASIN(SIN(X))/Y*S
         W0 = W+6. EXPO *EPS*ABS(Q0)
      ENDIF
      CALL WHET(Q,Q0,W0,X,Y,A,B,TS,TA)
      RETURN
      END
C
      SUBROUTINE WHET(Q,Q0,W0,X,Y,A,B,TS,TA)
      REAL Q,Q0,W0,X,Y,A,B
      CHARACTER*(*) TS,TA
C
C.... Test whether Q0.EQ.Q within +/- W0 (.GE.->.GT.)
C
      IF (ABS(Q-Q0).GT.W0) THEN
C
C....    Difference too big suggests P is not a constant after all.
C
         PRINT 4000,TS,X,')/',Y,' =',Q0,' differs from ',
     1      TA,A,')/',B,' =',Q,' too much.'
4000  FORMAT(/1X,4X,70('%')
     1   /1X,4X,A11,0PF38.1,A
     2   /1X,4X,11X,0PF38.1,A
     3   /1X,4X,11X,1PE45.37E3,A
     4   /1X,4X,1X,A10,0PF38.1,A
     5   /1X,4X,11X,0PF38.1,A
     6   /1X,4X,11X,1PE45.37E3,A
     7   /1X,4X,70('%')
     8   /)

      PRINT *,'I want to: call ucbfail'
C   call ucbfail
      ENDIF
      RETURN
      END
C
      SUBROUTINE DISPLA(J,A,B,C,E,R)
      INTEGER J
      REAL A,B,C,E,R
C
C     Display Formatting
C
C.... display  J, A, B, C, R, E
C
      PRINT 2000,J,A,B,C,R,E
2000  FORMAT(1X,I2,1X,F37.0,'/',F37.0
     1   /1X,2X,1X,27X,'+',1X,1PE45.37E3
     2   /1X,2X,1X,1X,1PE45.37E3,1X,'+/-',1PE16.8E3
     3   )
      RETURN
      END
C
      SUBROUTINE COMPAR(E,R)
      REAL E,R
C
C.... test for consistency
C
C.... local variables
C
      REAL E0,R0
      SAVE E0,R0
      DATA E0,R0/0.1416 EXPO ,0. EXPO /
C
C.... .LT.->.LE.
C
      IF (ABS(R-R0).LE.E+E0) THEN
     E0 = E
         R0 = R
      ELSE
         PRINT *,'Varying R implies defective argument reduction.'
         PRINT *,'I want to: call ucbfail'
C   call ucbfail
         STOP
      ENDIF
      RETURN
      END

Will update here with results for full ucb floating point test suite when I get it to compile & run.

[quaeler]

Same divergent results for macOS 10.12.6 (gfortran 6.3.0) v. Ubuntu 17.10 (gfortran 7.2.0) running on the same hardware (i7-5557U)

[lewisl]

Different symptoms but same problem here. Running MacOS 10.13.02. Running Python 3.6.0.

Tensorflow 1.4.1 produces not just different results but essentially erroneous results. A very simple conv_net fails to converge, but does converge with 1.2.1.

The sample data and the nn design come from the Coursera deeplearning.ai course sequence. They provide sandboxed Jupyter notebooks that run Python 3.5 with tensorflow 1.2.1.

Seems like a serious problem with tf 1.4.1, which seems to be latest version that PyPi provides with Python binding.

When 1.5 has released python bindings and a pre-compiled binary I'll give it a try.

[lewisl]

I can confirm that the same problem occurs with the latest (as of 1/20/2018) nightly build: 1.6.0-dev20180119. I'd say this problem is very severe. I am downgrading to 1.2.1.

[Gemesys]

Thanx quaeler and lewisl for posting your results. This gets more interesting and surprising the deeper we go. I had expected an upgrade to MacOS and Xcode+gfortran would probably resolve the divergence issue, but quaeler's results show this not to be the case. And lewisl's situation seems to confirm my worst fears - that this apparently tiny divergence could result in the failure of a network to train correctly.

The Fortran test program is part of a suite of tests from Univ. of California Berkeley, which I found on the Utah site, where a collection of floating-point arithmetic tests are located, its url is: http://www.math.utah.edu/~beebe/software/ieee/#other. The UCB test suite looks like it was developed by W. Kahan who worked on ("invented" might be the better term) the IEEE 754 arithmetic methods, and it was then extended by Sun Microsystems. This was a big issue back in 1995, when the first Pentium chip came to market, and was shown to have a critical flaw in it's floating-point hardware, where it would produce wrong results under certain special circumstances. Test suites were developed to verify floating-point math, and run multiple tests for both accuracy and consistancy of results.

The Utah software collection refers to the UCB test suite, and it can be downloaded as a tarball from: http://www.netlib.org/fp/ucbtest.tgz

I've downloaded this test suite, and converted enough of it to get it running on both the MacOS and CentOS-7.4. It is fairly comprehensive, and identifies several "ulp" differences - both on each machine, and between the two platforms. ("Ulp" is the term used which means "unit in the last place", and is considered a better measure and check of floating-point accuracy than the term "epsilon").. (Here is a note about 'ulp': https://www.jessesquires.com/blog/floating-point-swift-ulp-and-epsilon/ )

The "UCBTest" suite is useful in that it runs both C and Fortran programs, in both single-precision and double-precision (53 bit significance). I've converted it so it now compiles and runs on both 64-bit machines. (I might have made conversion errors, keep that in mind. There are compile warnings...)

For now, running the full test suite on both machines results in 47 out of 56 tests passing on the CentOS/HP box, and 45 out of 56 tests passing on the MacOS/MacBook. I am still checking details, but there is one program (which compiles into four different executables: cpar_SP, cpar_DP, fpar_SP and fpar_DP => c = C source, f = Fortran source, SP=single precision, DP=double precision), and the "par" refers to "paranoid" - implies you run this because you are concerned your numbers are not being calculated correctly! ). The results of all four "par" programs indicated "UCBPASS" on both machines, so there does not seem to be anything obviously wrong related to rounding and/or plus/minus infinity and the handling of "NaN" (not a number) values.

Attached screen images show results of the full UCBTest suite, run on each machine. Note that the "NME" and the "PME" (Negative Maximum and Postive Maximum ULP error observed) for the last test displayed (the LOG(X) test) is slightly different between each machine. Also, it took some effort to get the UCBTest suite to compile and run on each machine (some of the code is quite old), and the tests run directly from the Makefiles that are used to build the programs, which complicates conversion. Some of the "fails" could be due to conversion issues. But this suite of tests is comprehensive, and is highlighting other divergence issues. I want continue down this "rabbit-hole" until I can get a clearer sense of what is going on, and why the MacOS seems to be generating different results than the Linux platforms. We now know that both CentOS and Ubuntu - current versions - seem to agree on how they do their math - but the MacOS is producing different results.

I just want to caution that I might be making a mistake or an error in conversion, here. In an effort to factor out issues that might be related to the "gfortran" compiler, I have been looking at the results generated by the C programs. There appear to be cases where the divergence is serious. I want to make sure I am getting proper compile results on each platform.

[lewisl]

Let me know if there is more I can provide. I can provide the jupyter notebook of the python code if that would be helpful.

Thanks for all your serious digging.

• Lewis

On Jan 23, 2018, at 12:17 PM, GemesysCanada notifications@github.com<mailto:notifications@github.com> wrote:

Thanx quaeler and lewisl for posting your results. This gets more interesting and surprising the deeper we go. I had expected an upgrade to MacOS and Xcode+gfortran would probably resolve the divergence issue, but quaeler's results show this not to be the case. And lewisl's situation seems to confirm my worst fears - that this apparently tiny divergence could result in the failure of a network to train correctly.

The Fortran test program is part of a suite of tests from Univ. of California Berkeley, which I found on the Utah site, where a collection of floating-point arithmetic tests are located, its url is: http://www.math.utah.edu/~beebe/software/ieee/#otherhttp://www.math.utah.edu/%7Ebeebe/software/ieee/#other. The UCB test suite looks like it was developed by W. Kahan who worked on ("invented" might be the better term) the IEEE 754 arithmetic methods, and it was then extended by Sun Microsystems. This was a big issue back in 1995, when the first Pentium chip came to market, and was shown to have a critical flaw in it's floating-point hardware, where it would produce wrong results under certain special circumstances. Test suites were developed to verify floating-point math, and run multiple tests for both accuracy and consistancy of results.

The Utah software collection refers to the UCB test suite, and it can be downloaded as a tarball from: http://www.netlib.org/fp/ucbtest.tgz

I've downloaded this test suite, and converted enough of it to get it running on both the MacOS and CentOS-7.4. It is fairly comprehensive, and identifies several "ulp" differences - both on each machine, and between the two platforms. ("Ulp" is the term used which means "unit in the last place", and is considered a better measure and check of floating-point accuracy than the term "epsilon").. (Here is a note about 'ulp': https://www.jessesquires.com/blog/floating-point-swift-ulp-and-epsilon/ )

The "UCBTest" suite is useful in that it runs both C and Fortran programs, in both single-precision and double-precision (53 bit significance). I've converted it so it now compiles and runs on both 64-bit machines. (I might have made conversion errors, keep that in mind. There are compile warnings...)

For now, running the full test suite on both machines results in 47 out of 56 tests passing on the CentOS/HP box, and 45 out of 56 tests passing on the MacOS/MacBook. I am still checking details, but there is one program (which compiles into four different executables: cpar_SP, cpar_DP, fpar_SP and fpar_DP => c = C source, f = Fortran source, SP=single precision, DP=double precision), and the "par" refers to "paranoid" - implies you run this because you are concerned your numbers are not being calculated correctly! ). The results of all four "par" programs indicated "UCBPASS" on both machines, so there does not seem to be anything obviously wrong related to rounding and/or plus/minus infinity and the handling of "NaN" (not a number) values.

Attached screen images show results of the full UCBTest suite, run on each machine. Note that the "NME" and the "PME" (Negative Maximum and Postive Maximum ULP error observed) for the last test displayed (the LOG(X) test) is slightly different between each machine. Also, it took some effort to get the UCBTest suite to compile and run on each machine (some of the code is quite old), and the tests run directly from the Makefiles that are used to build the programs, which complicates conversion. Some of the "fails" could be due to conversion issues. But this suite of tests is comprehensive, and is highlighting other divergence issues. I want continue down this "rabbit-hole" until I can get a clearer sense of what is going on, and why the MacOS seems to be generating different results than the Linux platforms. We now know that both CentOS and Ubuntu - current versions - seem to agree on how they do their math - but the MacOS is producing different results.

I just want to caution that I might be making a mistake or an error in conversion, here. In an effort to factor out issues that might be related to the "gfortran" compiler, I have been looking at the results generated by the C programs. There appear to be cases where the divergence is serious. I want to make sure I am getting proper compile results on each platform. [screenshot_macos_full_ucbtest_2018-01-23_11d47am]https://user-images.githubusercontent.com/16905336/35289540-a180f9f6-0035-11e8-8cec-9f46d1b72d9d.png [screenshot_centos_run_ucbtest_23jan2018]https://user-images.githubusercontent.com/16905336/35289565-b1342652-0035-11e8-83dc-ef485944fd47.png

— You are receiving this because you commented. Reply to this email directly, view it on GitHubhttps://github.com/tensorflow/tensorflow/issues/15933#issuecomment-359861868, or mute the threadhttps://github.com/notifications/unsubscribe-auth/ABGLLbx0vHOJSGX1bwAkH4pPpWQtJOiRks5tNhQzgaJpZM4RVyqU.

[Gemesys]

It was possible that the gfortran compiler might be responsible for the divergence in results between MacOS and Linux, so here is the C version of Kahan's PIRATS test program. I basically just hacked it out of the UCBTest suite, and made a stand-alone version of it. It can be compiled and run on MacOS under Apple's gcc (on Macbook: "gcc --version" reports: LLVM 7.0.2 (clang-700.1.81)) and CentOS-7.4 Linux (Same results seen on Ubuntu also, as per what quaeler has reported). (My version of CentOS's gcc reports for "gcc --version": 4.8.5 20150623 (Red Hat 4.8.5-16)).

This C version of PIRATS shows the same divergence as the gFortran version does. I've provided it here, because it make it easier to run this on different machines to see what results are reported - i.e. no need to download and install a version of gfortran. Interestingly, the "single precision" versions of PIRATS generate results that are exactly the same across both machines. And the gfortran versions on both machines match exactly the C version results obtained on each machine. So, regardless of using C or gFortran, the same divergence is evident between MacOS and Linux. And based on quaeler's results, the divergence that PIRATS demostrates is evident across old and new versions of MacOS, versus current CentOS and Ubuntu Linux.

/*
C.... PIRATS                     Copyright (C) by W. Kahan, Mar. 8, 1989
C
C.... This program finds close rational approximations
C.... A/B to PI, and computes the differences C = PI-A/B to
C.... working precision within errors no bigger than E.  Working
C.... precision arithmetic is presumed to carry no more than about
C.... 110 sig. dec., and to be rounded reasonably like a DEC VAX
C.... or an HP calculator or in conformity with IEEE 754/854.
C.... Then the program tests argument reductions in functions SIN,
C.... COS and TAN, checking to see whether they are consistent
C.... with the hypothesis that their actual periods are some single
C.... close approximation 2*P to 2*PI if not 2*PI itself.
C
c     INTEGER NPI
c     PARAMETER (NPI = 210)
C
C.... The following array of NPI+1 divisors D(J) > 0 in the continued
C.... fraction PI = D(0)+1/(D(1)+1/(D(2)+1/(D(3)+...))) will incur an
C.... error in PI no worse than 3.6E-234. Only D(NPI) isn't an integer.
C.... This data is based upon DJ's computed by Stewart McDonald
C.... in 1983 from an algorithm due to W. Gosper.  W. K.
C
C --- Mod. standalone - Mark Langdon, GEMESYS Ltd., Waterloo, Jan.2018
C --- to check Clang/Xcode on MacOS versus gcc (GCC) 4.8.5 on CentOS-7.4 
C --- for # divergence related to curious behaviour of TensorFlow 1.4.1
*/

#include "ucbtest.h"

typedef long int integer;
typedef char *address;

typedef long ftnlen;

#define VOID void

#define abs(x) ((x) >= 0 ? (x) : -(x))
#define min(a,b) ((a) <= (b) ? (a) : (b))
#define aint(x) ((x>0) ? FLOOR(x) : -FLOOR(-x) )

/* Table of constant values */

static integer c__210 = 210;
static integer c__2 = 2;

/* Main program */ MAIN__()
{
    /* Initialized data */

    static GENERIC d[211] = { 3.,7.,15.,1.,292.,1.,1.,1.,2.,1.,3.,1.,14.,
        2.,1.,1.,2.,2.,2.,2.,1.,84.,2.,1.,1.,15.,3.,13.,1.,4.,2.,6.,6.,
        99.,1.,2.,2.,6.,3.,5.,1.,1.,6.,8.,1.,7.,1.,2.,3.,7.,1.,2.,1.,1.,
        12.,1.,1.,1.,3.,1.,1.,8.,1.,1.,2.,1.,6.,1.,1.,5.,2.,2.,3.,1.,2.,
        4.,4.,16.,1.,161.,45.,1.,22.,1.,2.,2.,1.,4.,1.,2.,24.,1.,2.,1.,3.,
        1.,2.,1.,1.,10.,2.,5.,4.,1.,2.,2.,8.,1.,5.,2.,2.,26.,1.,4.,1.,1.,
        8.,2.,42.,2.,1.,7.,3.,3.,1.,1.,7.,2.,4.,9.,7.,2.,3.,1.,57.,1.,18.,
        1.,9.,19.,1.,2.,18.,1.,3.,7.,30.,1.,1.,1.,3.,3.,3.,1.,2.,8.,1.,1.,
        2.,1.,15.,1.,2.,13.,1.,2.,1.,4.,1.,12.,1.,1.,3.,3.,28.,1.,10.,3.,
        2.,20.,1.,1.,1.,1.,4.,1.,1.,1.,5.,3.,2.,1.,6.,1.,4.,1.,120.,2.,1.,
        1.,3.,1.,23.,1.,15.,1.,3.,7.,1.,16.,1.338371961073448 };

    /* System generated locals */
    integer i__1;

    /* Local variables */
    static GENERIC a, b, c, e;
    static integer j;
    static GENERIC r;
    extern /* Subroutine */ int getce_();
    static GENERIC fl;
    extern /* Subroutine */ int displa_(), nextab_(), compar_(), envcns_(), 
        tstrig_();
    static integer inc;
    static GENERIC eps, rdx;

/* MCL --- remove for stand-alnone pi.c version: pi_new.c  
    ucbstart( __FILE__, __LINE__);
    default_precision();
       --- */

/* .... Environmental constants EPS, RDX, FL */

    (void) envcns_(&eps, &rdx, &fl);

/* .... for adequate accuracy */

    inc = (integer) (LOG(fl) / LOG(2.6));

/*      PRINT 1000 */
/* 1000  FORMAT(1X,'PIRATS: computes  PI = A/B+C and R = PI-P.'/ */
/*     1   /1X,1X,'J',1X,18X,'A',18X,'/',18X,'B' */
/*     2   /1X,2X,1X,27X,'+',5X,'C' */
/*     3   /1X,2X,1X,41X,'R',5X,'+/-',5X,'E' */
/*     4   ) */
    (void) printf(" PIRATS: computes  PI = A/B+C and R = PI-P.\n");

/* .... Initialize A, B */

    a = d[0];
    b = 1.;

    i__1 = 210 - inc + 5;
    for (j = 1; j <= i__1; ++j) {

/* .... Get next pair A, B */

    nextab_(&d[j], &a, &b);
    if (a > fl || b > fl) {
        goto L110;
    }

/* ....    Get C = PI-A/B+/-E */

    getce_(&c__210, &j, &inc, &eps, &fl, d, &c, &e);

/* ....    Get R = PI-P+/-E */

    tstrig_(&eps, &a, &b, &c, &e, &r);

/* ....    Display these numbers */

    displa_(&j, &a, &b, &c, &e, &r);

/* ....    Test them for consistency */

    compar_(&e, &r);
/* L100: */
    }
L110:
/*  PRINT *,'Fin' */

/* .... Normal termination. */

    printf("Confirming:  UCBPASS  \n");

/* --- MCL: remove for standalone ver:     (void) ucbpass( __FILE__, __LINE__); */

} /* MAIN__ */

#ifdef __STDC__
VOID s_cat(char *lp, char *rpp[], ftnlen rnp[], ftnlen *np, ftnlen ll)
#else
VOID s_cat(lp, rpp, rnp, np, ll) char *lp, *rpp[]; ftnlen rnp[], *np, ll;
#endif
{
ftnlen i, n, nc;
char *f__rp;

n = (int)*np;
for(i = 0 ; i < n ; ++i)
    {
    nc = ll;
    if(rnp[i] < nc)
        nc = rnp[i];
    ll -= nc;
    f__rp = rpp[i];
    while(--nc >= 0)
        *lp++ = *f__rp++;
    }
while(--ll >= 0)
    *lp++ = ' ';
}

/* Subroutine */ int envcns_(eps, rdx, fl)
GENERIC *eps, *rdx, *fl;
{
    /* System generated locals */
#ifdef __STDC__
volatile
#endif
    GENERIC d__1;

    /* Local variables */
#ifdef __STDC__
volatile
#endif
    static GENERIC h, t, u, v, x, y;

/* .... Environmental constants.  This subroutine computes */
/* ....    EPS = nextafter(1,2)-1 = 1.000...001-1 */
/* ....    RDX = RaDiX of floating-point arithmetic (2, 10, 16) */
/* ....    FL = RDX/EPS = last of consecutive floating-point integers */
/* ....                       among 1, 2, 3, ..., FL-2, FL-1, FL. */

/* .... local variables */

/* .... First seek EPS */

    t = TOGENERIC(4) / TOGENERIC(3) ;
    x = t - 1.;
    y = (d__1 = x + x - 1. + x, abs(d__1)) / 64.;
    *eps = 0.;
    if (y == 0.) {
/*   PRINT *,'Is 4/3 exact?' */
    printf(" Is 4/3 exact? \n");
    goto L299;
    }
L200:
    if (*eps != 0.) {
    goto L210;
    }
    u = y + 1.;
    *eps = u - 1.;
    y += y;
    goto L200;

/*     Now seek EPS/RDX = 1-nextafter(1,0) = 1-0.999...999 : */

L210:
    h = TOGENERIC(1) / TOGENERIC(2) ;
    t = TOGENERIC(2) / TOGENERIC(3) ;
    x = t - h;
    y = (d__1 = x + x - h + x, abs(d__1)) / 64.;
    v = 0.;
    if (y == 0.) {
/*   PRINT *,'Is 2/3 exact?' */
    printf(" Is 2/3 exact? \n");
    goto L299;
    }
L220:
    if (v != 0.) {
    goto L230;
    }
    u = h - y + h;
    v = h - u + h;
    y += y;
    goto L220;

/* .... in case Division is dirty */

L230:
    d__1 = *eps / v + 1e-4;
    *rdx = aint(d__1);
    if (*rdx < 2.) {
/*   PRINT 5000,'Radix =',RDX */
#ifdef QP
    printf(" Radix = %Lg \n",*rdx);
#else
    printf(" Radix = %g \n",*rdx);
#endif
/* L5000: */
    goto L299;
    }

/* .... Confirm that RDX = Radix of Floating-point arithmetic. */

    t = *rdx;
    x = 1.;

/* .... until X.EQ.0 or X.EQ.RDX */

L240:
    if (x != 1.) {
    goto L250;
    }
    t += t;
    u = t + 1.;
    x = u - t;
    goto L240;
L250:
    if (x == 0.) {
    y = 1.;
L260:
    if (x != 0.) {
        goto L270;
    }
    y += y;
    u = t + y;
    x = u - t;
    goto L260;
    }
L270:
    if (x != *rdx) {
/*         PRINT 6000,'Is Radix ',X,' or ',RDX,'?' */
#ifdef QP
    printf(" Is Radix %Lg or %Lg ? \n",x,rdx);
#else
    printf(" Is Radix %g or %g ? \n",x,rdx);
#endif
/* L6000: */
    goto L299;
    }

/* .... Confirm that FL = RDX/EPS: */

    *fl = *rdx;
    x = 1.;
L280:
    if (x != 1.) {
    goto L290;
    }
    *fl *= *rdx;
    u = *fl + 1.;
    x = u - *fl;
    goto L280;
L290:
    if (*fl * v == 1.) {
    return 0;
    }

/* .... ENVCNS cannot compute environmental constants correctly: */

/*      PRINT 3000,'Is FL ',FL,' or ',1. d0 /V,'?' */
#ifdef QP
        printf(" Is FL %Lg or %Lg ? \n",*fl,1.0/v);
#else
        printf(" Is FL %g or %g ? \n",*fl,1.0/v);
#endif
/* 3000  FORMAT(1X,A6,1PE45.37E3/1X,2X,A4,1PE45.37E3,A1) */
L299:
/*  PRINT *,'Subroutine ENVCNS cannot compute correctly the' */
/*      PRINT *,'Environmental constants' */
/*      PRINT *,'EPS = 1.000...001 - 1 , and' */
/*      PRINT *,'FL = Last consecutive Floating-point integer' */
/*      PRINT *,'        among 1, 2, 3, ..., FL-2, FL-1, FL.' */
/*      PRINT *,'Please substitute them for the subroutine.' */
    printf(" envcns cannnot compute correctly the Environmental constants. \n");
    printf("Confirming:  UCBFAIL  \n");
        /* MCL --- removed for standalone version. (void) ucbfail( __FILE__ , __LINE__ ); */
} /* envcns_ */

/* Subroutine */ int nextab_(dj, a, b)
GENERIC *dj, *a, *b;
{
    /* Initialized data */

    static GENERIC a0 = 1.;
    static GENERIC b0 = 0.;

    static GENERIC t;

/* .... Get next pair A, B */

/* .... local variables */

    t = *dj * *b + b0;
    b0 = *b;
    *b = t;
    t = *dj * *a + a0;
    a0 = *a;
    *a = t;

/* .... Now A/B = D0+1/(D1+1/(D2+...+1/DJ)). */

    return 0;
} /* nextab_ */

/* Subroutine */ int getce_(npi, j, inc, eps, fl, d, c, e)
integer *npi, *j, *inc;
GENERIC *eps, *fl, *d, *c, *e;
{
    /* System generated locals */
    integer i__1, i__2;

    /* Local variables */
    static integer i;
    static GENERIC x, y, z;
    static integer i9;

/* .... This subroutine computes the continued fraction's tail */
/* ....    Z = D(J+1)+1/(D(J+2)+1/(D(J+3)+1/(D(J+4)+...))) */
/* .... to working accuracy by using INC terms of it, and then */
/* .... computes the effect C of cutting it off to get A/B . */
/* .... */
/* .... Get  C = PI-A/B+/-E */

/* .... local variables */

/* Computing MIN */
    i__1 = *npi, i__2 = *j + *inc;
    i9 = min(i__1,i__2);
    z = d[i9];
    i__1 = *j + 1;
    for (i = i9 - 1; i >= i__1; --i) {
    z = d[i] + 1. / z;
/* L400: */
    }
    x = *fl * *fl;

/* .... C = 1/Z-1/X always */

    *c = 1. / z - 1. / x;
    for (i = *j; i >= 1; --i) {
    y = d[i];
    z = y + 1. / z;
    x = y + 1. / x;
    *c = -(*c) / (x * z);
/* L410: */
    }

/* .... E > accumulated roundoff (mixed arithmetic) */

    *e = *j * 4. * *eps * abs(*c);
    return 0;
} /* getce_ */

/* Subroutine */ int tstrig_(eps, a, b, c, e, r)
GENERIC *eps, *a, *b, *c, *e, *r;
{
    /* Initialized data */

    static char si[10+1] = "arcsin(sin";
    static char co[10+1] = "arcsin(cos";
    static char ta[10+1] = "arctan(tan";

    /* System generated locals */
    address a__1[2];
    integer i__1[2];
    GENERIC d__1, d__2;
    char ch__1[1];

    /* Local variables */
    extern /* Subroutine */ int whet_();
    static GENERIC q, s, w, x, y, q0, w0;
    static char ts[11];

/* .... Get R = PI-P+/-E */

/*     This subroutine tests whether the programs that compute */
/*     TRIG(X) = trig(X*PI/P) for TRIG = sin, cos or tan */
/*     always use the same approximation P to PI during their */
/*     argument reduction.  If so, 3 or 4 values R = Q+C */
/*     derived from A = B*(PI-C+/-E) ought to agree. */

/* .... local variables */

/* .... FNODD(floating-point integer X) = (-1)**X */

/* .... FNS(1) = '+', FNS(-1) = '-' */

    q = ATAN(TAN(*a)) / *b;
    *r = q + *c;
    w = *eps * 3. * abs(q);
    *e += w;
    d__1 = abs(*b) * .5 + .125;
    s = (aint(d__1) * 2. - abs(*b)) * 2. + 1.;
    x = *a;
    y = *b;
/* Writing concatenation */
    ch__1[0] = 44 - (integer) s;
    i__1[0] = 1, a__1[0] = ch__1;
    i__1[1] = 10, a__1[1] = si;
    s_cat(ts, a__1, i__1, &c__2, 11L);
    q0 = ASIN(SIN(x)) / y * s;
    w0 = w + *eps * 6. * abs(q0);
    whet_(&q, &q0, &w0, &x, &y, a, b, ts, ta, 11L, 10L);
    x = *a * .5;
    y = *b * .5;
    if (s < 0.) {

/* ....    (B+1) is even */

    d__1 = (*b + 1.) * .5;
    d__2 = abs(d__1) * .5 + .125;
    s = (aint(d__2) * 2. - abs(d__1)) * 2. + 1.;
/* Writing concatenation */
    ch__1[0] = 44 - (integer) s;
    i__1[0] = 1, a__1[0] = ch__1;
    i__1[1] = 10, a__1[1] = co;
    s_cat(ts, a__1, i__1, &c__2, 11L);
    q0 = ASIN(COS(x)) / y * s;
    w0 = w + *eps * 6. * abs(q0);
    } else {

/* ....    B = 2y is even */

/* Writing concatenation */
    i__1[0] = 1, a__1[0] = " ";
    i__1[1] = 10, a__1[1] = ta;
    s_cat(ts, a__1, i__1, &c__2, 11L);
    q0 = ATAN(TAN(x)) / y;
    w0 = *eps * 3. * abs(q0);
    whet_(&q, &q0, &w0, &x, &y, a, b, ts, ta, 11L, 10L);
    d__1 = abs(y) * .5 + .125;
    s = (aint(d__1) * 2. - abs(y)) * 2. + 1.;
/* Writing concatenation */
    ch__1[0] = 44 - (integer) s;
    i__1[0] = 1, a__1[0] = ch__1;
    i__1[1] = 10, a__1[1] = si;
    s_cat(ts, a__1, i__1, &c__2, 11L);
    q0 = ASIN(SIN(x)) / y * s;
    w0 = w + *eps * 6. * abs(q0);
    }
    whet_(&q, &q0, &w0, &x, &y, a, b, ts, ta, 11L, 10L);
    return 0;
} /* tstrig_ */

/* Subroutine */ int whet_(q, q0, w0, x, y, a, b, ts, ta, ts_len, ta_len)
GENERIC *q, *q0, *w0, *x, *y, *a, *b;
char *ts, *ta;
ftnlen ts_len;
ftnlen ta_len;
{
    /* System generated locals */
    GENERIC d__1;

/* .... Test whether Q0.EQ.Q within +/- W0 (.GE.->.GT.) */

    if ((d__1 = *q - *q0, abs(d__1)) > *w0) {

/* ....    Difference too big suggests P is not a constant after all. 
*/

/*         PRINT 4000,TS,X,')/',Y,' =',Q0,' differs from ', */
/*     1      TA,A,')/',B,' =',Q,' too much.' */
/* 4000  FORMAT(/1X,4X,70('%') */
/*     1   /1X,4X,A11,0PF38.1,A */
/*     2   /1X,4X,11X,0PF38.1,A */
/*     3   /1X,4X,11X,1PE45.37E3,A */
/*     4   /1X,4X,1X,A10,0PF38.1,A */
/*     5   /1X,4X,11X,0PF38.1,A */
/*     6   /1X,4X,11X,1PE45.37E3,A */
/*     7   /1X,4X,70('%') */
/*     8   /) */
#ifdef QP
    printf(" %s %Lg / %Lg  differs from %s %Lg / %Lg = %Lg too much.\n",
#else
    printf(" %s %g / %g  differs from %s %g / %g = %g too much.\n",
#endif
        ts,*x,*y,*q0,ta,*a,*b,*q);

    printf("Confirming:  UCBFAIL  \n");
        /* MCL --- Removed for standalone version: (void) ucbfail( __FILE__ , __LINE__ ); */
    }
    return 0;
} /* whet_ */

/* Subroutine */ int displa_(j, a, b, c, e, r)
integer *j;
GENERIC *a, *b, *c, *e, *r;
{

/*     Display Formatting */

/* .... display  J, A, B, C, R, E */

/*      PRINT 2000,J,A,B,C,R,E */
/* 2000  FORMAT(1X,I2,1X,F37.0,'/',F37.0 */
/*     1   /1X,2X,1X,27X,'+',1X,1PE45.37E3 */
/*     2   /1X,2X,1X,1X,1PE45.37E3,1X,'+/-',1PE16.8E3 */
/*     3   ) */
#ifdef QP
    printf(" J %3d A %37.0Lf / B %37.0Lf + C %45.37Le \n",
        *j,*a,*b,*c);
    printf(" J %3d R %45.37Le +- %17.9Le \n",
        *j,*r,*e);
#endif
#ifdef DP
    printf(" J %2d A %17.0f / B %17.0f + C %25.17e \n",
        *j,*a,*b,*c);
    printf(" J %2d R %25.17e +- %17.9e \n",
        *j,*r,*e);
#endif
#ifdef SP
    printf(" J %2d A %9.0f / B %9.0f + C %17.9e \n",
        *j,*a,*b,*c);
    printf(" J %2d R %17.9e +- %17.9e \n",
        *j,*r,*e);
#endif
    return 0;
} /* displa_ */

/* Subroutine */ int compar_(e, r)
GENERIC *e, *r;
{
    /* Initialized data */

    static GENERIC e0 = .1416;
    static GENERIC r0 = 0.;

    /* System generated locals */
    GENERIC d__1;

/* .... test for consistency */

/* .... local variables */

/* .... .LT.->.LE. */

    if ((d__1 = *r - r0, abs(d__1)) <= *e + e0) {
    e0 = *e;
    r0 = *r;
    } else {
/*         PRINT *,'Varying R implies defective argument reduction.' 
*/
    printf(" Varying R implies defective argument reduction. \n");
    printf("Confirming:  UCBFAIL  \n");
        /* --- MCL removed for standalone version: (void) ucbfail( __FILE__ , __LINE__ ); */
    }
    return 0;
} /* compar_ */

/* Main program alias */ int main () { MAIN__ (); }

You will also need this file: ucbtest.h

#ifndef _UCBTEST

#define _UCBTEST

/*  special definitions for Sun test harness    */

#ifdef SP
#undef SP
#define FLOAT
#endif

#ifdef DP
#undef DP
#define DOUBLE
#endif

#ifdef QP
#undef QP
#define LONGDOUBLE
#endif

#ifndef SUN_IEEE
#if (sunpro_version >= 100) || (sunos_version/100 == 4)
#define SUN_IEEE
#endif
#endif

#ifndef SUN_MATH
#if (sunpro_version >= 300)
#define SUN_MATH
#endif
#endif

/*  Global macro definitions.   */

#ifdef PC
#define FINT    long        /* C equivalent of Fortran integer */
#define INT32   long        /* 32 bit int */
#define UINT32  unsigned long   /* 32 bit unsigned */
#else
#define FINT    int     /* C equivalent of Fortran integer */
#define INT32   int     /* 32 bit int */
#define UINT32  unsigned int    /* 32 bit unsigned */
#endif

#ifdef SUN_MATH
#include <sunmath.h>
#endif
#include <math.h>

#ifndef NTESTS
#define NTESTS 1000000L   /* DOS wants L specifier added */
#endif

#if defined(__STDC__) || defined(DOS)
#define ANSI_PROTOTYPES
#define PROTO(p)  p
#else
#undef ANSI_PROTOTYPES
#define PROTO(p)  ()
#endif

#ifdef FLOAT
#define SP
#define GENERIC float
#define GENERIC_STRING "float"
#define PRECISION_STRING "single"
#define ABS(X) fabs((double)(X))
#define MOD(X,Y) fmod((double)(X),(double)(Y))
#define CEIL(X) ceil((double)(X))
#define FLOOR(X) floor((double)(X))
#if defined(__STDC__) && !defined(NO_FUNCF)
#define SQRT(X) sqrtf((float)(X))
#define LOG(X) logf((float)(X))
#define SIN(X) sinf((float)(X))
#define COS(X) cosf((float)(X))
#define TAN(X) tanf((float)(X))
#define ASIN(X) asinf((float)(X))
#define ACOS(X) acosf((float)(X))
#define ATAN(X) atanf((float)(X))
#define POW(X,Y) powf((float)(X),(float)(Y))
extern float sqrtf(float);
extern float logf(float);
extern float sinf(float);
extern float cosf(float);
extern float tanf(float);
extern float asinf(float);
extern float acosf(float);
extern float atanf(float);
extern float powf(float,float);
#else
#define SQRT(X) sqrt((double)(X))
#define LOG(X) log((double)(X))
#define SIN(X) sin((double)(X))
#define COS(X) cos((double)(X))
#define TAN(X) tan((double)(X))
#define ASIN(X) asin((double)(X))
#define ACOS(X) acos((double)(X))
#define ATAN(X) atan((double)(X))
#define POW(X,Y) pow((double)(X),(double)(Y))
#endif
#endif

#ifdef DOUBLE
#define DP
#define GENERIC double
#define GENERIC_STRING "double"
#define PRECISION_STRING "double"
#define ABS(X) fabs((double)(X))
#define MOD(X,Y) fmod((double)(X),(double)(Y))
#define CEIL(X) ceil((double)(X))
#define FLOOR(X) floor((double)(X))
#define SQRT(X) sqrt((double)(X))
#define LOG(X) log((double)(X))
#define SIN(X) sin((double)(X))
#define COS(X) cos((double)(X))
#define TAN(X) tan((double)(X))
#define ASIN(X) asin((double)(X))
#define ACOS(X) acos((double)(X))
#define ATAN(X) atan((double)(X))
#define POW(X,Y) pow((double)(X),(double)(Y))
#endif

#ifdef LONGDOUBLE
#define QP
#define GENERIC long double
#define GENERIC_STRING "long double"
#define PRECISION_STRING "extended"
#define ABS(X) fabsl((long double)(X))
#define MOD(X,Y) fmodl((long double)(X),(long double)(Y))
#define CEIL(X) ceill((long double)(X))
#define FLOOR(X) floorl((long double)(X))
#define SQRT(X) sqrtl((long double)(X))
#define LOG(X) logl((long double)(X))
#define SIN(X) sinl((long double)(X))
#define COS(X) cosl((long double)(X))
#define TAN(X) tanl((long double)(X))
#define ASIN(X) asinl((long double)(X))
#define ACOS(X) acosl((long double)(X))
#define ATAN(X) atanl((long double)(X))
#define POW(X,Y) powl((long double)(X),(long double)(Y))
extern long double fabsl(long double);
extern long double fmodl(long double, long double);
extern long double ceill(long double);
extern long double floorl(long double);
extern long double sqrtl(long double);
extern long double logl(long double);
extern long double sinl(long double);
extern long double cosl(long double);
extern long double tanl(long double);
extern long double asinl(long double);
extern long double acosl(long double);
extern long double atanl(long double);
extern long double powl(long double, long double);
#endif

#define TOGENERIC(X) ((GENERIC)(X))
#define ZERO ((GENERIC)(0))
#define ONE  ((GENERIC)(1))
#define TWO  ((GENERIC)(2))
#define FOUR ((GENERIC)(4))

extern UINT32 ntests, nregions;
extern UINT32 significand_length;

/*  IEEE features with machine-dependent syntax     */

extern void round_nearest PROTO((void));
extern void round_positive PROTO((void));
extern void round_zero PROTO((void));
extern void generic_precision PROTO((void));
extern void default_precision PROTO((void));

/*  Common ucbtest functions            */

extern void ucbstart PROTO((char *file,int line));
extern void ucbfail PROTO((char *file,int line));
extern void ucbpass PROTO((char *file,int line));

#include "stdio.h"

#ifdef sunos_version

#if (sunos_version/100 >= 4)
#include "stdlib.h"
#endif

#else
#include "stdlib.h"
#endif

#ifndef __NEWVALID
extern UINT32 get_significand PROTO((void));
extern void ucbdivtest_ PROTO((int *, char **));
extern void ucbmultest_ PROTO((int *, char **));
extern void ucbsqrtest_ PROTO((int *, char **));
extern void ucbfindpitest_ PROTO((int *, char **));
extern void ucbeeftest_ PROTO((int *, char **));
#endif

#endif /* _UCBTEST */

The PIRATS program can be compiled in "double-precision" mode using this file:

compile_pi_new_c_DP

#!/bin/sh
#
# --- pre-process and compile the pi_new.c program to executable: pinewcDP
#
# (((((((((((((((  Double Precision Verson  )))))))))))))))
gcc -cpp -D DP  pi_new.c -lm -o pinewcDP

# --- you can run "pinewcDP" stand-alone, and check if it passes or fails.
# --- if it passes, it will say: "Confirming: UCBPASS". 

If you want to run the test in single-precision (32-bit instead of 64-bit), you can do it with this:

compile_pi_new_c_SP

#!/bin/sh
#
# --- pre-process and compile the pi_new.c program to executable: pinewcSP
#
# (((((((((((((((  Single Precision Verson  )))))))))))))))
gcc -cpp -D SP  pi_new.c -lm -o pinewcSP

# --- you can run "pinewcSP" stand-alone, and check if it passes or fails.
# --- if it passes, it will say: "Confirming: UCBPASS". 

I'll make a more detailed review of the UCBTest suiite, and post the results here. It would seem to me the differences between MacOS and Linux results have to be affecting TensorFlow, in more areas than just PDE simulations and image-creation, as lewisl's post indicates is happening.

[tensorflowbutler]

The original poster has replied to this issue after the stat:awaiting response label was applied.

[Gemesys]

Cracked it. Got a solution (workaround, essentially), and a probable cause. The MacBook running MacOS Yosemite (10.10.5) looks to be doing it's rounding and/or floating-point math wrong. Based on Quaeler's results which shows the simulation running on MacOS Sierra 10.12.6 same as on Linux platforms (CentOS-7.4 and Ubuntu), it's clear the evolution of the Laplace PDE (partial differential equation) simulation to the complex moire-pattern is the correct evolution, and the MacOS Yosemite 10.10.5 has a flaw in how it is doing 32-bit floating math. On GNU Linux systems, both 32-bit and 64-bit (CentOS-6.6 and CentOS-7.4 confirmed) it is possible to explicitly control precision, using a routine "fesetprec", which can be lifted from a handbook of code: (see here) https://books.google.ca/books?id=OjUyDwAAQBAJ&pg=PA127&lpg=PA127&dq=ieee.c+++fesetprec+to+control+precision&source=bl&ots=VLtoiOfYfE&sig=BfdtySalckBzIB-mbV_Uy4uXLL4&hl=en&sa=X&ved=0ahUKEwjD1r6BzujYAhUH94MKHTNhDowQ6AEIJzAA#v=onepage&q=ieee.c%20%20%20fesetprec%20to%20control%20precision&f=false

The "fesetprec" invokes a macro, called: "_FPU_SETCW", which generates some assembler code to set values in the Intel control word which, on IA-32 architectures, is used to explicitly control precision of floating point calculations. The macro's _FPU_GETCW and _FPU_SETCW are available on GNU Linux systems in the "fpu_control.h" include file, in /usr/include. The Intel spec for 8087 and 80387 FPU's allowed this. The newer/newest MMX (and now SSE and SSE2 and SSE3 and such) architectures are indicated as not using this control word -but curiously, if you run test programs to explicity set precision, and then run precision-dependent code, you can see that on both architectures - IA-32, and the newer 64-bit Intel Core-i3 and Core-i5 chips, this control word can still be set, at least on Linux machines. I've confirmed this.

I downloaded and converted the UCBTest suite which exercises a bunch of floating-point calculations, and then I also pulled together a working example of a test program (from the Handbook previously mentioned), which sets the precison control-word. Basically, you define your vars as "long double", but then you can tweak the control-word to run in float, double, or long-double. The test program "chkprec.c" gives three different results, depending on the precision selected. This program works the same on both CentOS 6.6 and CentOS 7.4. Long-double on a 32-bit box is probably going to be compiled as REAL*10 (the 80-bit extended precision - which Intel chips do their math in - and which has been a fixture of Intel architecture since the first IBM P/C.) I know a tiny bit about this, because my "gDOSbox" app (free, no ads, no tracking on Google Playstore) is special, because I know it has had its conversion math fixed so that mapping from 32-bit ("float"), and 64-bit (double precision) to 80-bit (extended precision), was not originally being done correctly, (in the open-source DOSbox code), but is being done correctly in gDOSbox. Most public DOSbox's would not run high-precision Fortran or C progams correctly. The math in "gDOSbox" can be run correctly, and the APL interpreters and Fortran compilers that it supports (WF77 - Watcom Fortran is one of them), do their math correctly (I've checked).

For NN (Neural Net) applications, matrix-math must be done correctly, and the TensorFlow Laplace sim was a great exercise of matrix math. The routine used is called: "tf.nn.depthwise_conv2d" (if you import TensorFlow into Python as "tf"). It is documented here: https://www.tensorflow.org/api_docs/python/tf/nn/depthwise_conv2d

You might also want to look at this, if learning about tf.nn.depthwise_conv2d: https://github.com/tensorflow/tensorflow/blob/r1.5/tensorflow/python/ops/nn_impl.py

What I found using UCBTest and chkprec.c, was that the Macbook Pro, under Yosemite (MacOS 10.10.5) does not support the explicit-setting of precision in the same manner that Linux does. There is no provision for setting the precision control-word on the Mac under Yosemite, or if there is, it is substantially different than is the case for Linux. My version of chkprec.c on the MacBook is an ugly hack, with three different functions, one in each precision level (float, double, and long double), and it was only in this way that I could reproduce the results I was getting on Linux, where the precision control word could be set to the desired precision using fsetprec. This means that math-calc code written for Linux which relies on the ability to explicitly control precision, probably won't run correctly on the Mac, unless low-level changes are made. Also, there are differences in the "UCBfail"s that occur on the Macbook, as opposed to the Linux boxes. What is interesting, is the 64-bit Linux runs the UCBTest suite better than the 32-bit Linux (CentOS 6.6) does. And both the Linux 64-bit and the MacOS 64-bit pass the cpar_DP and cpar_SP ("paranoid") tests, as well as the DP and SP (double and single precision) tests for "mul" and "div". But the "cpi_DP" test iterates differently on Mac versus Linux 64-bit, and only in a few places where the exponents are large negative (E-26, E-38, E-40, and such).

I will post the various test programs to my github account.

In order to get the Laplace PDE simulation to iterate-and-evolve correctly (so you get a funky image of a moire-pattern, and some dark-matter black-space, instead of just a blank screen, as the MacBook was doing), I changed all the 32-bit ("float" level precision, like REAL4 in Fortran), into 64-bit doubles (like REAL8 in Fortran). The TensorFlow documentation indicates that the tf.nn.depthwise_conv2d is able to operate in either mode, and it does. It appears that TensorFlow is operating correctly, and it appears the bug that shows up in MacOS only manifests itself if the Python (numpy) variables are 32-bit (or "float).

Change all the variables to 64-bit, and the simulation works the same on both machines. I'll monitor this thread for a bit, and if the TensorFlow authors don't close it, I will, as it appears not to be a TensorFlow issue, but is a MacOS issue, which as Quaeler discovered, can be resolved by upgrading to MacOS 10.12.6 (Sierra), and probably the newer "High Sierra" as well. If you have other reasons for wishing to maintain your MacBook at Yosemite, but still want to run TensorFlow (in CPU mode), then I would recommend doing your network math and back-propagations with 64-bit floats, not 32-bit values. I ran the sim forward with 57500 iterations, and the exponents are up around E+132 and E+133... big numbers, but still calculating correctly. The final image and numeric (U(eval) at row 20) images for MacBook and Linux (CentOS-7.4) provided below.

Hope all this helps anyone else struggling with wrong floating-point number problems on their MacBooks using TensorFlow. The problem likely resides somewhere in the Xcode 7.2.1 - Clang 700x compiler used to build Python and TensorFlow, and again, is most likely resolved by using later versions of the compiler where the floating-point flaws appear to have been corrected. (But they aren't all fixed. Some of the test programs we have tried still show variance between Linux and MacOS results. The "PIRATS" program (see above) still shows some different numbers on each platform.)

In my work with Xerion, I found it was critical to set the TCL-precision variable to it's highest value (17 or 18 or some such thing), if I wanted to write the network-weights out to a file, for subsequent loading at a later time, if the file was an ascii (not binary) numeric represetation. The default was 8 digits after the decimal, and if you wrote and re-read network weights at that precision, your network was destroyed. Weight digits 10 or 12 past the decimal place made a difference to network operation, and it became clear a very high level of precision was essential. If you are working with neural networks, you might want to read W. Kahan's paper from his IEEE 754 lecture. https://people.eecs.berkeley.edu/~wkahan/ieee754status/IEEE754.PDF It illustrates some of the issues and edge-case conditions that floating-point calculations run up against, and the choices and trade-offs that were made to create a viable floating-point calculation standard. It is a good paper, and it provides background on why floating-point calculations can fail to operate as expected. (Images of Laptest_64 sim on each platform follow..)

[quaeler]

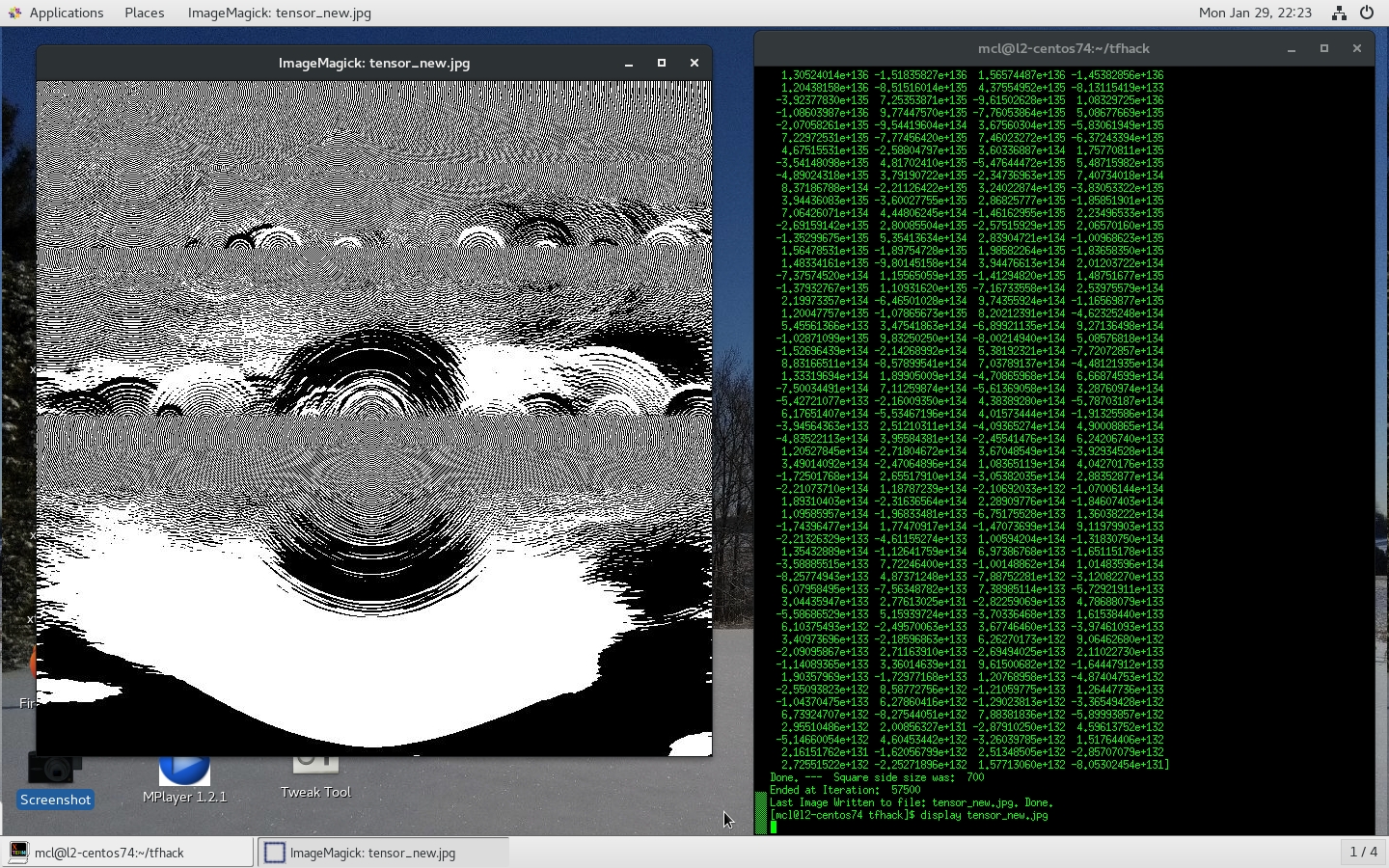
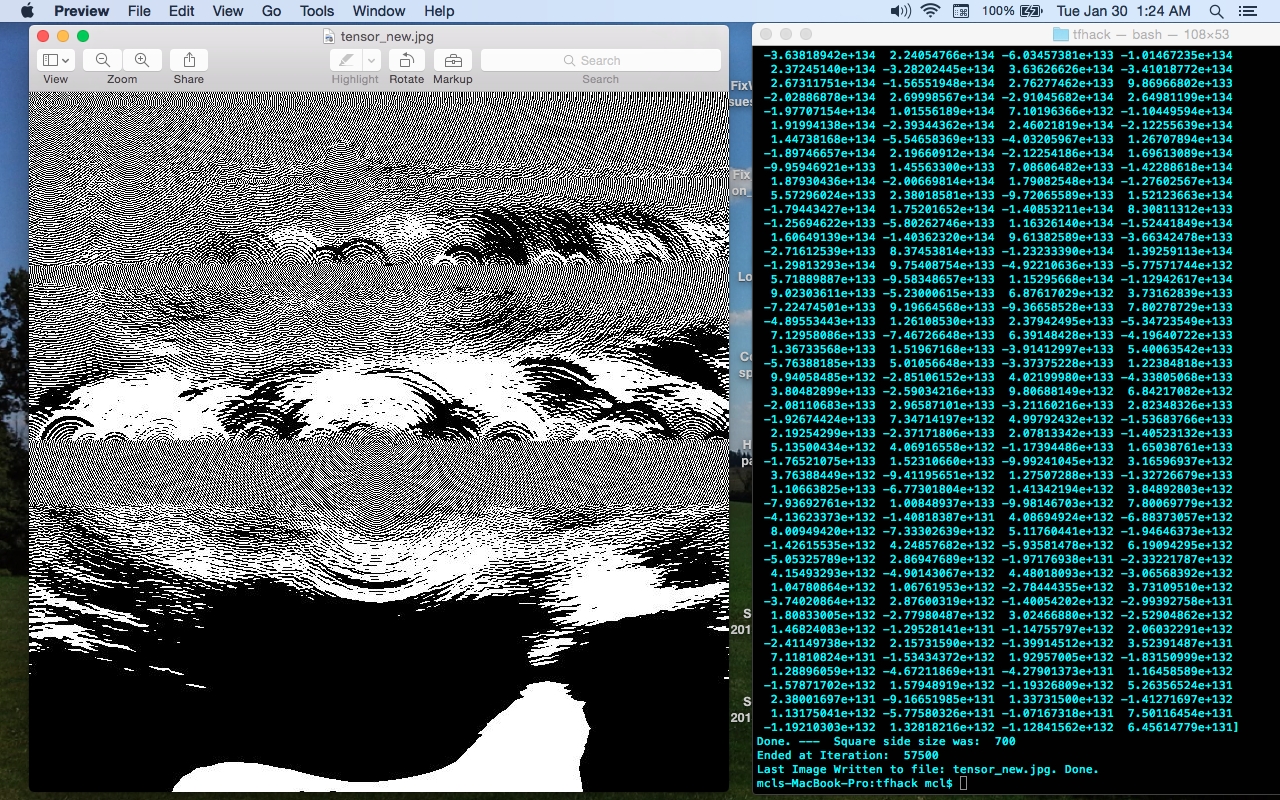
(a) This is excellent work - thank you. (b) On the larger scale of things, I don't know what one does with this information in a helpful manner (for TF or otherwise.) It should be disseminated so that it is definitely "public knowledge", but I'm short on a useful idea how to do this. @cy89 ? @martinwicke ?

[lewisl]

Thanks for putting so much work into this. Really helps with the underlying cause.

On a somewhat discouraging note I’ll point out that upgrading MacOS very likely won’t help. The symptoms I saw—a conv-net that won’t converge (cost and accuracy remaining flat regardless of number of epochs of SDG—occur with higher versions of tensorflow on MacOS High Sierra 10.13.3 (the latest).

I’ll try re-ihstalling tf 1.4.1 and making all the numpy arrays 64 bit and see what happens and report back.

Again, thanks for all of your work on this.

On Jan 30, 2018, at 9:11 PM, GemesysCanada notifications@github.com<mailto:notifications@github.com> wrote:

Cracked it. Got a solution (workaround, essentially), and a probable cause. The MacBook running MacOS Yosemite (10.10.5) looks to be doing it's rounding and/or floating-point math wrong. Based on Quaeler's results which shows the simulation running on MacOS Sierra 10.12.6 same as on Linux platforms (CentOS-7.4 and Ubuntu), it's clear the evolution of the Laplace PDE (partial differential equation) simulation to the complex moire-pattern is the correct evolution, and the MacOS Yosemite 10.10.5 has a flaw in how it is doing 32-bit floating math. On GNU Linux systems, both 32-bit and 64-bit (CentOS-6.6 and CentOS-7.4 confirmed) it is possible to explicitly control precision, using a routine "fesetprec", which can be lifted from a handbook of code: (see here) https://books.google.ca/books?id=OjUyDwAAQBAJ&pg=PA127&lpg=PA127&dq=ieee.c+++fesetprec+to+control+precision&source=bl&ots=VLtoiOfYfE&sig=BfdtySalckBzIB-mbV_Uy4uXLL4&hl=en&sa=X&ved=0ahUKEwjD1r6BzujYAhUH94MKHTNhDowQ6AEIJzAA#v=onepage&q=ieee.c%20%20%20fesetprec%20to%20control%20precision&f=false

The "fesetprec" invokes a macro, called: "_FPU_SETCW", which generates some assembler code to set values in the Intel control word which, on IA-32 architectures, is used to explicitly control precision of floating point calculations. The macro's _FPU_GETCW and _FPU_SETCW are available on GNU Linux systems in the "fpu_control.h" include file, in /usr/include. The Intel spec for 8087 and 80387 FPU's allowed this. The newer/newest MMX (and now SSE and SSE2 and SSE3 and such) architectures are indicated as not using this control word -but curiously, if you run test programs to explicity set precision, and then run precision-dependent code, you can see that on both architectures - IA-32, and the newer 64-bit Intel Core-i3 and Core-i5 chips, this control word can still be set, at least on Linux machines. I've confirmed this.

I downloaded and converted the UCBTest suite which exercises a bunch of floating-point calculations, and then I also pulled together a working example of a test program (from the Handbook previously mentioned), which sets the precison control-word. Basically, you define your vars as "long double", but then you can tweak the control-word to run in float, double, or long-double. The test program "chkprec.c" gives three different results, depending on the precision selected. This program works the same on both CentOS 6.6 and CentOS 7.4. Long-double on a 32-bit box is probably going to be compiled as REAL*10 (the 80-bit extended precision - which Intel chips do their math in - and which has been a fixture of Intel architecture since the first IBM P/C.) I know a tiny bit about this, because my "gDOSbox" app (free, no ads, no tracking on Google Playstore) is special, because I know it has had its conversion math fixed so that mapping from 32-bit ("float"), and 64-bit (double precision) to 80-bit (extended precision), was not originally being done correctly, (in the open-source DOSbox code), but is being done correctly in gDOSbox. Most public DOSbox's would not run high-precision Fortran or C progams correctly. The math in "gDOSbox" can be run correctly, and the APL interpreters and Fortran compilers that it supports (WF77 - Watcom Fortran is one of them), do their math correctly (I've checked).

For NN (Neural Net) applications, matrix-math must be done correctly, and the TensorFlow Laplace sim was a great exercise of matrix math. The routine used is called: "tf.nn.depthwise_conv2d" (if you import TensorFlow into Python as "tf"). It is documented here: https://www.tensorflow.org/api_docs/python/tf/nn/depthwise_conv2d

You might also want to look at this, if learning about tf.nn.depthwise_conv2d: https://github.com/tensorflow/tensorflow/blob/r1.5/tensorflow/python/ops/nn_impl.py

What I found using UCBTest and chkprec.c, was that the Macbook Pro, under Yosemite (MacOS 10.10.5) does not support the explicit-setting of precision in the same manner that Linux does. There is no provision for setting the precision control-word on the Mac under Yosemite, or if there is, it is substantially different than is the case for Linux. My version of chkprec.c on the MacBook is an ugly hack, with three different functions, one in each precision level (float, double, and long double), and it was only in this way that I could reproduce the results I was getting on Linux, where the precision control word could be set to the desired precision using fsetprec. This means that math-calc code written for Linux which relies on the ability to explicitly control precision, probably won't run correctly on the Mac, unless low-level changes are made. Also, there are differences in the "UCBfail"s that occur on the Macbook, as opposed to the Linux boxes. What is interesting, is the 64-bit Linux runs the UCBTest suite better than the 32-bit Linux (CentOS 6.6) does. And both the Linux 64-bit and the MacOS 64-bit pass the cpar_DP and cpar_SP ("paranoid") tests, as well as the DP and SP (double and single precision) tests for "mul" and "div". But the "cpi_DP" test iterates differently on Mac versus Linux 64-bit, and only in a few places where the exponents are large negative (E-26, E-38, E-40, and such).

I will post the various test programs to my github account.

In order to get the Laplace PDE simulation to iterate-and-evolve correctly (so you get a funky image of a moire-pattern, and some dark-matter black-space, instead of just a blank screen, as the MacBook was doing), I changed all the 32-bit ("float" level precision, like REAL4 in Fortran), into 64-bit doubles (like REAL8 in Fortran). The TensorFlow documentation indicates that the tf.nn.depthwise_conv2d is able to operate in either mode, and it does. It appears that TensorFlow is operating correctly, and it appears the bug that shows up in MacOS only manifests itself if the Python (numpy) variables are 32-bit (or "float).

Change all the variables to 64-bit, and the simulation works the same on both machines. I'll monitor this thread for a bit, and if the TensorFlow authors don't close it, I will, as it appears not to be a TensorFlow issue, but is a MacOS issue, which as Quaeler discovered, can be resolved by upgrading to MacOS 10.12.6 (Sierra), and probably the newer "High Sierra" as well. If you have other reasons for wishing to maintain your MacBook at Yosemite, but still want to run TensorFlow (in CPU mode), then I would recommend doing your network math and back-propagations with 64-bit floats, not 32-bit values. I ran the sim forward with 57500 iterations, and the exponents are up around E+132 and E+133... big numbers, but still calculating correctly. The final image and numeric (U(eval) at row 20) images for MacBook and Linux (CentOS-7.4) provided below.

Hope all this helps anyone else struggling with wrong floating-point number problems on their MacBooks using TensorFlow. The problem likely resides somewhere in the Xcode 7.2.1 - Clang 700x compiler used to build Python and TensorFlow, and again, is most likely resolved by using later versions of the compiler where the floating-point flaws appear to have been corrected. (But they aren't all fixed. Some of the test programs we have tried still show variance between Linux and MacOS results. The "PIRATS" program (see above) still shows some different numbers on each platform.)

In my work with Xerion, I found it was critical to set the TCL-precision variable to it's highest value (17 or 18 or some such thing), if I wanted to write the network-weights out to a file, for subsequent loading at a later time, if the file was an ascii (not binary) numeric represetation. The default was 8 digits after the decimal, and if you wrote and re-read network weights at that precision, your network was destroyed. Weight digits 10 or 12 past the decimal place made a difference to network operation, and it became clear a very high level of precision was essential. If you are working with neural networks, you might want to read W. Kahan's paper on IEEE 754, and the choices and trade-offs that were made to create a viable floating-point math standard. (Images of Laptest_64 sim on each platform follow..) [laptest_64_700_centos74_screenshot_2018-01-29_10_32pm]https://user-images.githubusercontent.com/16905336/35584502-34d92556-05c3-11e8-9485-b8629e501347.jpg [laptest_64_700_57k_macos_screenshot_2018-01-30_1_24am]https://user-images.githubusercontent.com/16905336/35584523-46e5b3b8-05c3-11e8-92c3-8cf00b9bb8ab.jpg

— You are receiving this because you commented. Reply to this email directly, view it on GitHubhttps://github.com/tensorflow/tensorflow/issues/15933#issuecomment-361699391, or mute the threadhttps://github.com/notifications/unsubscribe-auth/ABGLLW_4IC2Z9S4xQ2BvfxcMKWwYPXD-ks5tP2legaJpZM4RVyqU.

[quaeler]

@skye awaiting response or awaiting tensorflower?

[skye]

Ah sorry, I didn't read through the thread carefully enough. @lewisl thank you for digging into this and finding a solution! @MarkDaoust are you in charge of docs? It sounds like there are numerical problems running TF on MacOS Yosemite, which we may wanna warn about in the docs (see @lewisl's comment above this one, starting with "Cracked it.").

[MarkDaoust]

Wow this is quite a thread... what would be the right way to document this? A note on the install_mac page? Can someone with a little more context suggest the text?

[cy89]

Wow indeed: @Gemesys, this is excellent numerical detective work!

@MarkDaoust I think that the install_mac page is a good place to start. It seems to me like our baseline requirement is already MacOS X 10.11 (El Capitan) or higher.

The most numerically conservative thing to do would be to raise the minimum required version to 10.12.6 (Sierra) as @Gemesys reports. That seems pretty narrow, as Sierra has only been out since 13 June 2016.

If we don't want to make TF drop support for El Capitan early, then I'd suggest making the recommendation line longer:

* macOS X 10.11 (El Capitan or higher) is supported. Note that there are accuracy-affecting numerical issues before macOS X 10.12.6 (Sierra) that are described in [GitHub#15933](https://github.com/tensorflow/tensorflow/issues/15933#issuecomment-366331383), so 10.12.6 or higher is preferred. 

[martinwicke]

I'm happy to drop support for El Capitan. Apple is pretty good about making sure people can upgrade, the upgrades are free, and I'd think not too many users remain on El Capitan. I would still add a warning to the install page to motivate it, since installation will actually work fine.

Note that there are known accuracy-affecting numerical issues before macOS X 10.12.6 (Sierra) that are described in [GitHub#15933](https://github.com/tensorflow/tensorflow/issues/15933#issuecomment-366331383). 

[bjacob]

It would be interesting to find out more about how the OS can play any role here. After all, the floating-point control word is a CPU feature, not an OS feature. There have been cases where OSes or drivers still managed to corrupt such CPU state by means of interrupts, or alternatively, one could imagine that some OS might have a buggy implementation of saving/restoring registers in context-switches... it would be interesting to find that out.

[bignamehyp]

Is this issue resolved after the fix?

[tensorflowbutler]

Nagging Awaiting Response: It has been 14 days with no activityand the awaiting response label was assigned. Is this still an issue?

[MarkDaoust]

Is this issue resolved after the fix?

The docs are updated on versions/master/ is that a sufficient resolution?