Lakonik
commented
2 years ago Yes the likelihood is not a PDF. Likelihood has nothing to do with density. Only after applying the Bayesian rule can the posterior become a PDF.
Closed TheCuriousJoe closed 2 years ago
Lakonik
commented
2 years ago Yes the likelihood is not a PDF. Likelihood has nothing to do with density. Only after applying the Bayesian rule can the posterior become a PDF.
TheCuriousJoe
commented
2 years ago Yes the likelihood is not a PDF. Likelihood has nothing to do with density. Only after applying the Bayesian rule can the posterior become a PDF.
The likelihood function is not as normal as usual. Can u give me more detail about how to get equation(2) from equation(1)? Or there is not a strictly math induction?
Lakonik
commented
2 years ago If you strictly consider the likelihood to be the conditional probability density of X, then Eq. (2) is incomplete because a normalization factor is missing. But this is OK because it's being used as a likelihood and its absolute scale doesn't matter.
TheCuriousJoe
commented
2 years ago Thanks a lot. Excellent work again and wish I could figure out all the equations and intuitions.
Hi HanSheng, very excellent work! In equation (2), likelihood fuction p(X|y) is defined as=e^{-\frac{1}{2}\sum_{i=1}^{N}||f(y_i)||^2} "https://latex.codecogs.com/png.image?\huge \dpi{50}p(X|y)=e^{-\frac{1}{2}\sum_{i=1}^{N}||f(y_i)||^2}")
.
We can view p(X|y) as the joint probability of p(X1|y), ... , p(X2|y). So =e^{-\frac{1}{2}{}||f(y_i)||^2} "https://latex.codecogs.com/png.image?\huge \dpi{50}p(X_i|y)=e^{-\frac{1}{2}{}||f(y_i)||^2}")
.
||fi(y)|| is reprojective error and its value from 0 to infinity. Let x be ||fi(y)||, 
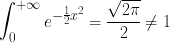. So p(Xi|y) is not a pdf.
Is my induction correct? If my induction is correct, statement p(X|y) is not proper here. And following equation can't use Bayes theorem to get p(y|X).
Perhaps i'm splitting hairs, but it really confused me.