Graph Classification & Batchwise Training

[rushilanirudh]

Hi I have two questions:

• I would like to repurpose this for graph classification (where I have a single label per graph). I see there is an option to choose featureless=False when defining a new GraphConvolution layer. However, the loss is still computed for each node, and I was wondering how I should change your code.
• In the context of graph classification, how should I modify your train.py for batch-wise training?

Thanks for putting this together!

[tkipf]

Thanks for your questions. For graph-level classification you essentially have two options:

• "hacky" version: you add a global node to the graph that is connected to all other nodes and run the standard protocol. You can then interpret the final value of this global node as graph-level label.
• global pooling: as a last layer, you can implement a global pooling layer that performs some form of pooling operation (optionally with attention mechanism as in https://arxiv.org/abs/1511.05493) over all graph nodes

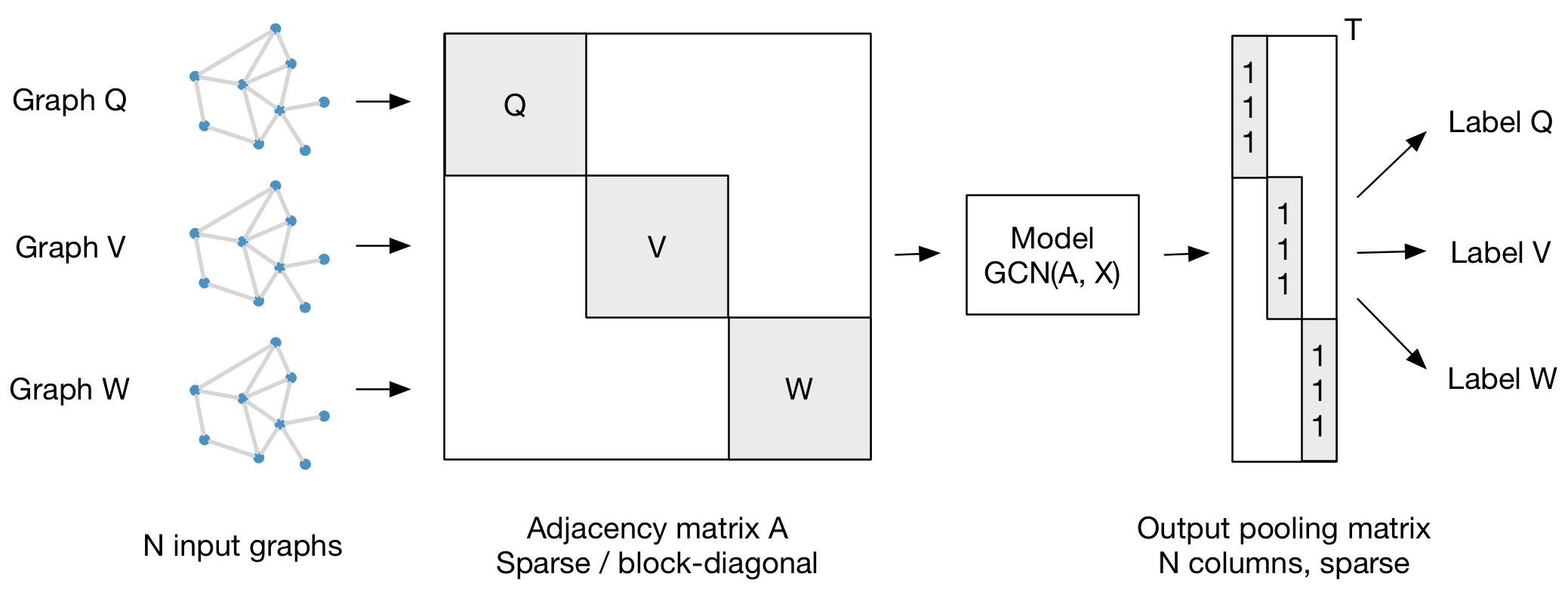
For batch-wise training over multiple graph instances (of potentially different size) with an adjacency matrix each, you can feed them in the form of a block-diagonal adjacency matrix (each block corresponds to one graph instance) to the model, as illustrated in the figure below:

[aravindsankar28]

Hi,

I have a followup question here. Though the code has a featureless option, I do not think it works directly when featureless is set to True. I just wanted to confirm that.

Thanks for your great code !

[tkipf]

Hi, thanks for the catch. For the featureless mode, you have to set the input dimension of the first layer (only the first layer supports featureless) to be the number of nodes in the graph. I'll make sure to add a sentence or two about this in the documentation at some point.

[liuguoping]

Hi,

I want to use this gcn framework to do a semi-supervised regression mission (Given a graph(V, E) with feature matrix, the value(continuous) of some node is known while others are not, Target: predict the value of those unknown nodes). I directly change the loss function into RMSE, but it doesn't work well on validation dataset and test dataset. so,

• is GCN suitable for regression?

• how to change this framework to meet the requirements of regression?

Thanks you !

[michaelosthege]

As far as I know regression should work. But you may want to look at the A-normalization. If I remember correctly, the normalization method proposed by Kipf & Welling does not lead to the rows of the normalized adjacency summing to 1.

[tkipf]

It might be a good idea to turn the regression problem into a classification problem by bucketing the real-valued targets into several classes. This typically (empirically) works quite well in combination with a (softmax) cross-entropy loss. See, e.g., the WaveNet paper (https://arxiv.org/abs/1609.03499) for details.

[huanglianghua]

It might also work to cast the regression problem as a classification problem by augmenting the input data similar to support vector regression. For example, regression from x to y, can be converted to a classification task with data ([x, y+r], 1) and ([x, y-r], -1). Thus no need to change the normalization term.

[tkipf]

That sounds interesting. What would 'r' be in this case?

[huanglianghua]

'r' is a manually set real-value margin, e.g., r = 0.8. The setting of 'r' typically depends on the range of y (to ensure most/all features are separable) and how much you'd like the samples to be separable. See here for details, where r is the epsilon in this case.

[pasinit]

Hi, it is not clear to me how to give to the model a batch of graphs instead of only one. Could you please give other details? Thanks

[michaelosthege]

Hi @tommy9114,

If I remember correctly (last time I touched it was in April) it is not possible to forward-pass multiple graphs at once, because you'd need a rank>2 sparse Tensor. Attempts were made to support rank>2 sparse Tensors with tensorflow (https://github.com/tensorflow/tensorflow/pull/9373) but it did not work out.

So if you want to pass multiple graphs at once, you should find out if any of the other frameworks (PyTorch?) support rank>2 sparse Tensors.

[tkipf]

This is not quite correct, you can build a block-diagonal sparse matrix representing multiple graph instances at once. You further need to introduce a sparse gathering matrix that pools representations from their according graphs. All this can be done with regular sparse-dense matrix multiplications (of rank 2). Let me know if you need further details to implement this! On Mon 18. Dec 2017 at 17:43 michaelosthege notifications@github.com wrote:

Hi @tommy9114 https://github.com/tommy9114,

If I remember correctly (last time I touched it was in April) it is not possible to forward-pass multiple graphs at once, because you'd need a rank>2 sparse Tensor. Attempts were made to support rank>2 sparse Tensors with tensorflow (tensorflow/tensorflow#9373 https://github.com/tensorflow/tensorflow/pull/9373) but it did not work out.

So if you want to pass multiple graphs at once, you should find out if any of the other frameworks (PyTorch?) support rank>2 sparse Tensors.

— You are receiving this because you commented.

Reply to this email directly, view it on GitHub https://github.com/tkipf/gcn/issues/4#issuecomment-352483155, or mute the thread https://github.com/notifications/unsubscribe-auth/AHAcYO2TyQEbFrZWHiD5tBmer9iKcr7rks5tBpYWgaJpZM4LofoM .

[pasinit]

yea in fact I previously read about this block-diagonal sparse matrix but actually I don't really know what is it and how to create it. I didn't find anything on google about how to build such data structure.

[tkipf]

The following figure should hopefully clarify the idea:

[pasinit]

Oh, great thanks!

On Wed, Dec 20, 2017 at 9:53 AM, Thomas Kipf notifications@github.com wrote:

The following figure should hopefully clarify the idea: [image: graph_classification] https://user-images.githubusercontent.com/7347296/34198685-8c48e1d2-e56b-11e7-8ce6-64f1ba8a655c.png

— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHub https://github.com/tkipf/gcn/issues/4#issuecomment-353002759, or mute the thread https://github.com/notifications/unsubscribe-auth/AHMXGsWFLJMy4Fm2CH8jT2VJ1LZACLf-ks5tCMsDgaJpZM4LofoM .

-- Tommaso Pasini Ph.D. Student, Linguistic Computing Laboratory (LCL) Computer Science Department Sapienza University of Roma Room: F13 - via Regina Elena 295 palazzina F, 00161 Rome, Italy. Homepage: http://wwwusers.di.uniroma1.it/~pasini/ http://www.tommasopasini.altervista.org/

[mleming]

@tkipf Sorry to beat this into the ground. But, I'm interested in classifying about 2000 (i.e., N = 2000) 100x100 adjacency matrices (representing graphs) into two different classes -- i.e., whole-graph labelling. Going by your figure, this means that I ought to feed it a sparse 200,000 x 200,000 adjacency matrix into the model (i.e., each of the 2000 graphs represented along the diagonal). And the output pooling matrix is 200,000 x 2000, with the class labels along the diagonals (i.e., where the 1's are in your figure). Is this correct or am I completely missing something?

[tkipf]

This is correct, but I would recommend training the model using smaller mini-batches of, say, 32 or 64 graphs each. Make sure the pooling matrix is also sparse and that you're using sparse-dense matrix multiplications wherever possible. This should run quite fast in practice. Good luck!

[pasinit]

@mkeming Can I ask you if your graphs have the same node set (all the graphs have the same nodes) but different edges, or each graph has different nodes?

Best

On Thu, Jan 4, 2018 at 10:48 PM, Thomas Kipf notifications@github.com wrote:

This is correct, but I would recommend training the model using smaller mini-batches of, say, 32 or 64 graphs each. Make sure the pooling matrix is also sparse and that you're using sparse-dense matrix multiplications wherever possible. This should run quite fast in practice. Good luck!

— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHub https://github.com/tkipf/gcn/issues/4#issuecomment-355408464, or mute the thread https://github.com/notifications/unsubscribe-auth/AHMXGqMD-KiG0M_MMLft-v0dYDWx4SHwks5tHUc_gaJpZM4LofoM .

-- Tommaso Pasini Ph.D. Student, Linguistic Computing Laboratory (LCL) Computer Science Department Sapienza University of Roma Room: F13 - via Regina Elena 295 palazzina F, 00161 Rome, Italy. Homepage: http://wwwusers.di.uniroma1.it/~pasini/ http://www.tommasopasini.altervista.org/

[mleming]

@tommy9114 Same nodes and number of nodes, different edge values.

[pasinit]

i see, thanks

On Fri, Jan 5, 2018 at 11:19 AM, mleming notifications@github.com wrote:

@tommy9114 https://github.com/tommy9114 Same nodes and number of nodes, different edge values.

— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHub https://github.com/tkipf/gcn/issues/4#issuecomment-355520472, or mute the thread https://github.com/notifications/unsubscribe-auth/AHMXGikQanQhd5tkg4tKbXs9FpPSJ9IGks5tHfc-gaJpZM4LofoM .

-- Tommaso Pasini Ph.D. Student, Linguistic Computing Laboratory (LCL) Computer Science Department Sapienza University of Roma Room: F13 - via Regina Elena 295 palazzina F, 00161 Rome, Italy. Homepage: http://wwwusers.di.uniroma1.it/~pasini/ http://www.tommasopasini.altervista.org/

[tqvinhcs]

Hi, does anyone successfully use this for graph classification? I implement a toy example on mnist using each pixel as node and its intensity as feature. However, the loss did not go down? I have modified the graphconv layer to dense matrix to work with parallel data loader. And the "ind" (size: N*batch, values are normalized to the number of nodes in each graph) is the pooling matrix as in the figure

class GCN(nn.Module):

def __init__(self, dropout):
    super(GCN, self).__init__()
    self.gc1 = GraphConv(1, 16)
    self.gc2 = GraphConv(16, 32)
    self.fc1 = nn.Linear(32, 500)
    self.fc2 = nn.Linear(500, 10)

    self.dropout = dropout

def forward(self, x, adj, ind):
    # Conv layer
    x = F.relu(self.gc1(x, adj))
    x = F.relu(self.gc2(x, adj))

    # Batching before fc layer
    x = torch.mm(ind, x)

    # FC layers
    x = F.relu(self.fc1(x))
    x = F.dropout(x, self.dropout, training=self.training)
    x = self.fc2(x)

    return x

[tkipf]

I used this model quite some time ago for graph-level classification of the datasets provided in this paper: https://arxiv.org/abs/1605.05273 and got comparable (sometimes worse, sometimes better) results compared to their method. So maybe just have a look at these datasets. Shouldn't be too hard to load them in and run the model on these.

[mleming]

I edited your Keras Graph convolution code (train.py) and got something working, though it doesn't work incredibly well. I am still a little confused. The model in train.py (again, in the Keras version) takes both the adjacency matrix and the features of the graph. However, I wish to train on the adjacency matrices themselves, so the feature matrix would be unnecessary. And, for turning all of the node labels into a single graph label (for classification purposes), should we simply take the average of the node labels and go with the maximum? With the code as it is, I am still unsure how this would work well for whole-graph classification.

On 8 January 2018 at 09:04, Thomas Kipf notifications@github.com wrote:

I used this model quite some time ago for graph-level classification of the datasets provided in this paper: https://arxiv.org/abs/1605.05273 and got comparable (sometimes worse, sometimes better) results compared to their method. So maybe just have a look at these datasets. Shouldn't be too hard to load them in and run the model on these.

— You are receiving this because you commented. Reply to this email directly, view it on GitHub https://github.com/tkipf/gcn/issues/4#issuecomment-355912795, or mute the thread https://github.com/notifications/unsubscribe-auth/ACuN4w6F1ePthUKZCMC1sY9wQ2EMnIqAks5tIdoogaJpZM4LofoM .

[tkipf]

In order to go from node-level representation to a graph-level representation you will indeed have to perform some kind of order-invariant pooling operation. Any popular pooling strategy typically works fine, in my experience: attentive pooling (https://arxiv.org/abs/1703.03130) often works better than max pooling which in turn often works better than average pooling. Make sure to allocate a somewhat large representation size for the pre-pooling layer (as you're going to average a lot of values). You can also pool the representation of every layer individually and concatenate or add/average the result (similar to https://arxiv.org/abs/1509.09292).

If you don't have any initial node features, simply use an identity matrix (assuming the identity and position of every node is the same across all the graph samples) as an initial feature matrix. This essentially provides a unique one-hot feature vector for every node in the graph. Only works if node identities stay the same across all graph samples. Otherwise you will have to come up with some sensible feature representation (e.g. node degree, betweenness centrality, etc.).

[pasinit]

Sorry to keep asking question but I'm not sure if I got the right intuition: The architecture is able to learn feature vectors for nodes only if I pass always the same graph right? If my training set has different graphs (assume they have all the same dimension) but each row in the adj matrix may represents a different node then this architecture is not a good fit to learn the fetures of the nodes right? Thanks for your patient and kind answers

[tkipf]

No worries! Your intuition is correct in the absence of any node features, i.e. if you pick an identity matrix for the initial feature matrix. If, however, you describe nodes by features (from a feature space which is shared by all nodes, i.e. two nodes could have the same features) the model can learn from different graphs (e.g. molecules), such as done here: https://arxiv.org/abs/1509.09292

[pasinit]

Ok very interesting, so the features could also be derived from the graph itself (degree, centrality, number of triangles that contains it etc.) right?

On Fri, Jan 12, 2018 at 11:44 AM, Thomas Kipf notifications@github.com wrote:

No worries! Your intuition is correct in the absence of any node features, i.e. if you pick an identity matrix for the initial feature matrix. If, however, you describe nodes by features (from a feature space which is shared by all nodes, i.e. two nodes could have the same features) the model can learn from different graphs (e.g. molecules), such as done here: https://arxiv.org/abs/1509.09292

— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHub https://github.com/tkipf/gcn/issues/4#issuecomment-357205568, or mute the thread https://github.com/notifications/unsubscribe-auth/AHMXGoT0vVdcTWtnLdXTxdccKLPDM30Yks5tJzeqgaJpZM4LofoM .

-- Tommaso Pasini Ph.D. Student, Linguistic Computing Laboratory (LCL) Computer Science Department Sapienza University of Roma Room: F13 - via Regina Elena 295 palazzina F, 00161 Rome, Italy. Homepage: http://wwwusers.di.uniroma1.it/~pasini/ http://www.tommasopasini.altervista.org/

[tkipf]

Yes, sure! https://arxiv.org/abs/1509.09292 uses node degree as an initial feature, for example.

[pinkfloyd06]

Hello, @rushilanirudh @tkipf have you succeeded to update the code to deal with graph classification (rather than node classification. Each graph has only one class)?

Thank you

[tkipf]

I do not intend to release this implementation as part of this repository. But it shouldn't be too difficult to implement this yourself :-)

Edit: PRs are welcome

[pasinit]

I've implemented a self-attention layer:

class SelfAttention(Layer):
    def __init__(self, attention_dim, bias_dim, hidden_units, **kwargs):
        super().__init__(**kwargs)
        self.hidden_units = hidden_units
        self.A = None
        self.vars['Ws'] = tf.Variable(tf.random_uniform([attention_dim, self.hidden_units]))
        self.vars['W2'] = tf.Variable(tf.random_uniform([bias_dim, attention_dim]))

    def _call(self, inputs):
        aux = tf.tanh(tf.matmul(self.vars['Ws'], inputs, transpose_b=True))
        self.A = tf.nn.softmax(tf.matmul(self.vars['W2'], aux))
        tf.summary.histogram('self_attention', self.A)
        out = tf.matmul(self.A, inputs)
        out = tf.reshape(out, [out.get_shape().as_list()[0] * out.get_shape().as_list()[1]])
        return out

you can stack it on top of the gc layers. (Not sure if it is 100% correct, if you find something wrong please tell me!) Best,

[pinkfloyd06]

@tommy9114 Thank you for you answer. It looks ok (but l confirm when testing). So have you modified the loss function so that the loss is computer on the whole graph rather than at each node ?

[pasinit]

The attention layer take all the nodes embeddings into account and build a weighted average (where the weights are learnt) of those outputing a single hidden vector that should represent the whole graph. You can stack another dense layer with softmax to do the classification

[pinkfloyd06]

So as a last layer on the top of graph convolutional layers you add an attention layer (equation 7 in https://arxiv.org/pdf/1511.05493.pdf) then we add a dense layer with softmax to do classification. This process allows to keep the loss function (primarily defined to be applied at node level ) for graph classification. Correct me if l'm wrong !

[pasinit]

I don't know the paper you cited (thanks for the pointer it looks very interesting). I don't think we can keep the same loss function because it was developed to deal with multiple classifications (each node had his hown prediction). Now we have only one prediction so we can use a classical cross-entropy function (i think)

[pinkfloyd06]

l thought we talk about the same attention layer mechanism. So for you, what did you mean by the attention layer (without the pointer l gave), is it implemented here ?

[pasinit]

I used self-attention implemented here https://arxiv.org/pdf/1703.03130.pdf as @tkipf suggested in som post above i think

[pinkfloyd06]

@tommy9114 okey. So, to recap , adding attention layer on the top of GC (as you just mentionned) followed by a dense layer with softmax allows to keep unchanged the loss implemented to do graph classification ?

[pasinit]

I don't remember which loss is implemented in this repository but probably not. If i recall well in this repository we have a sigmoid activation function with the consequent sigmoid_cross_entropy. If you want to do single-label classification you better change it in order to use softmax at the and and softmax corss-entropy as loss function

On Tue, Mar 6, 2018 at 12:35 PM, pinkfloyd06 notifications@github.com wrote:

@tommy9114 https://github.com/tommy9114 okey. So, to recap , adding attention layer on the top of GC (as you just mentionned) followed by a dense layer with softmax allows to keep unchanged the loss implemented to do graph classification ?

— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHub https://github.com/tkipf/gcn/issues/4#issuecomment-370753378, or mute the thread https://github.com/notifications/unsubscribe-auth/AHMXGk8cUcziYf1vkB41PILSG3BpNo27ks5tbnSAgaJpZM4LofoM .

-- Tommaso Pasini Ph.D. Student, Linguistic Computing Laboratory (LCL) Computer Science Department Sapienza University of Roma Room: F13 - via Regina Elena 295 palazzina F, 00161 Rome, Italy. Homepage: http://wwwusers.di.uniroma1.it/~pasini/ http://www.tommasopasini.altervista.org/

[pinkfloyd06]

Definitely, softmax cross entropy will do the job

[pinkfloyd06]

@tommy9114 , l'm wondering why there is no pooling layer in this graph convolutional network ?

[pasinit]

I think that @tkipf can answer better than me to this question!

[tkipf]

@pinkfloyd06 Pooling on graphs hasn't been convincingly shown yet to help in predictive performance. With pooling I mean hierarchical pooling, i.e. forming a hierarchy of coarser graphs. That's why we don't consider it here for simplicity. Using global pooling (like the implementation by @tommy9114 ) is still a very good idea, though.

[pinkfloyd06]

@tkipf Thank you for your answer. l have a follow up questions related to your comment.

1) How do you explain the fact of not using any pooling layer and your network performs ? 2) How do you explain that a hierarchy of coarser graph pooling doesn't help in predictive performance ? Is it related to the hierarchy itself or the way we build this hierarchy (adding fake node) ? 3) l would be very happy to give me a pointer to global pooling and its implementation on a graph . Thank you for the idea , l didn't heard about it before (global pooling on graph) @tommy9114

[tkipf]

This is getting off-topic. For global pooling the pointer by @tommy9114 is a good start: https://arxiv.org/pdf/1703.03130.pdf . Hierarchical pooling typically doesn't work well because you have to define some heuristic structure-based fixed pooling operation ahead of time. What kind of coarsening strategy works well will be highly domain dependent. There's currently no silver bullet that works well for all kinds of graph data.

[pinkfloyd06]

@tkipf thank you for your answer. It seems to be a good idea to apply a global pooling.

l would like to hear from @tommy9114 about that and his global pooling implementation on graphs.

[diliu1992]

Hi, I have two questions:

• When I want to use batch-wise training, is it right that I can't give to the model a batch of graphs(and y), unless I concatenate the all the X together and make a sparse block matrix A as input (just treat them as a big graph)?
• When I use your method(a sparse block A), I think I should concatenate my X and y in format of (M+...+Z) FeatNum and (M+...+Z)classNum, and A is a sparse block matrix. Could you tell me if I am right and give some guidance? Thanks

[tkipf]

Yes, this is correct.

If you do not need sparse matrix operations (in case your graphs are quite small), you can resort to a much simpler implementation by creating an adjacency tensor of shape BxNxN where B is the batch size and N is the maximum number of nodes a graph has in this batch. You will need to add row- and column-wise zero-padding if you have graphs of different size in a single batch. The form of the updates for the GCN model in this case should be easy to derive. Hope this helps!

[ghost]

Could you please explain in more details about implementation of graph classification? Thank you!

[tkipf]

Do you have any specific questions? On Sun 15. Jul 2018 at 09:40 Hung Nguyen notifications@github.com wrote:

Could you please explain in more details about implementation of graph classification? Thank you!

— You are receiving this because you were mentioned.

Reply to this email directly, view it on GitHub https://github.com/tkipf/gcn/issues/4#issuecomment-405073633, or mute the thread https://github.com/notifications/unsubscribe-auth/AHAcYGR4umETdq7FrOuJFZ-I9ul9Pvl4ks5uGvIEgaJpZM4LofoM .