search

tomilov / quickhull

Header-only single-class implementation of Quickhull algorithm for convex hulls finding in arbitrary dimension (>1) space.
https://habr.com/ru/articles/245221/
70 stars 8 forks source link

How does the algorithm perform in higher dimensions? (e.g. 7D sphere in R^8) #8

Closed sgbaird closed 2 years ago

sgbaird commented 4 years ago

HI Anatoliy,

The question you asked about internal ray facet intersections on the stack exchange a while ago is something I've been referencing in conjunction with MATLAB's implementation of the quickhull algorithm (convhulln) in order to find the facet in which a unit vector on a hypersphere intersects. The curse of dimensionality comes into play, as once I have the 8D coordinates of various points on a "quadrant" of a hypersphere with coarse discretization (see 3D analogue), the code is unlikely to complete (stuck in infinite loop, or just taking a really long time, e.g. 10+ hrs before I quit) or is unable to find an appropriate intersecting facet (probably an issue with precision of the inversion of the "P" matrix to get barycentric coordinates). I can get reasonable resolution, behavior, & performance up to 7D with a 6D hypersphere quadrant, but run into the issues mentioned above as soon as I'm in 8D (too coarse, can't find intersecting facet, or algorithm hangs/takes too long).

3D analogue: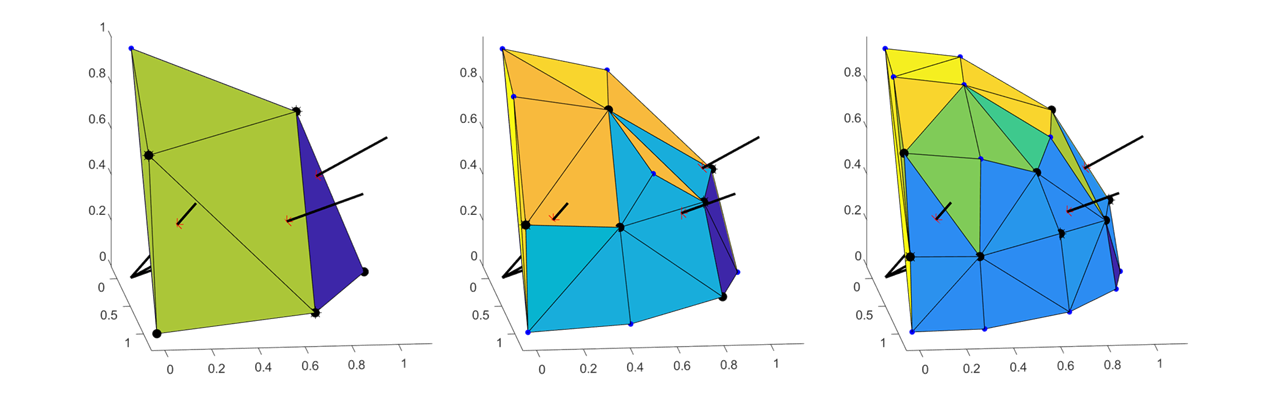 image

Given that, I'm wondering how this algorithm might perform using 8D points and if you have other general suggestions. What I mainly want is to know, given a random point on the hypersphere, the vertices of a facet that contains (the projection) of that datapoint so that I can perform interpolation (either through weighted averages using a distance metric, barycentric coordinates, generalized barycentric coordinates, etc.). I'll probably be posting a related stackexchange question as well.

Sterling

tomilov commented 4 years ago

Hi, @sgbaird. I think the key problem is bad numerical stability of the algorithm. Even matrix multiplication can lead to growth of relative error to unacceptable values. I would suggest to rewrite the algorithm from MATLAB/Octave language to Python and Jupyter Notebook using SageMath. It better to use another fileds for numeric data type (from here). Some of them have exact representation for results or (technically) infinite precision. As a side note, I think it is possible to project points from that part of D-sphere to D-1-simplex (that spans on the corner points) if you deal with a single hyperorthant. It can be simplier to work on the hyperplane, then to work on the hypersphere (say, triangulation vs convex hull). Barycentrics and other linear things should be the same.

tomilov commented 4 years ago

I found there is inversion of matrix (\ operator) in the algorithm. This is the worst place, which strongly affetcs numerical stability of the whole algorithm.

sgbaird commented 4 years ago

Hi @tomilov I agree that numerical stability seems to play a large part. I've been trying to use MATLAB's vpa() function (variable-precision arithmetic), but unfortunately even with 32-digit precision, there are still occasional cases on a 5-sphere and higher where no intersecting facet is found. If this is the issue, perhaps I will try the Python resource you mentioned.

I think your suggestion of reducing the dimensionality of the D-sphere by one would help quite a bit, especially since the 7-sphere seems to be just out of reach in certain ways. Do you have any suggestions for how to go about that projection/dimensionality-reduction? Also, thank you - I've been wondering what the analogue of a quadrant is in N-D (i.e. hyperorthant).

In your most recent comment, did you mean you found a matrix inversion (\ operator) in your quickhull implementation, MATLAB's convhulln(), the general quickhull algorithm, or the procedure for determining the intersecting facet? I use the \ operator in determining barycentric coordinates for the facet plane, and this seems like the most likely culprit for intersecting facets not being found. I wonder if it's just a matter of increasing precision, but I can probably only do this up to a certain point based on computational constraints (looking to do hyperdimensional barycentric interpolation on 10,000+ points).

Thank you for the help!

tomilov commented 4 years ago

I thought the entire source question didn't apply to this repository. This repository has two algorithms: Quickhull itself and algorithm (after Mehlhorn) to check convexity of resulting structure. The second one contains finding the intersection of a ray and a face, iirc. I didn't have any problems with numerical stability in dimensions up to 10 inclusive, I think. At least I don't remember the problem with misses on random generated data. There is no explicit inverse of a matrix. Just Gaussian elimination with pivoting, iirc. Default numeric data type in MATLAB/Octave is double. I am also use double in development of the code from this repository. I suspect that problem may be not in numerical errors. Maybe some omissions in implementation play a role?

sgbaird commented 4 years ago

It turns out you were right about numerical errors not being the issue. I was able to diagnose at least the issue of not finding the intersecting facet. It turned out that my approach of using only the facets containing the nearest neighbor to the datapoint sometimes fails when a non-uniform mesh is used (see my stackexchange question: Numerical Instability in Projective-based Barycentric Coordinates in High Dimensions). I still haven't solved the issue of convhulln() taking too long or "hanging", and so I will probably try your quickhull implementation and make the # of meshpoints adjustable in finer increments to see if the performance improves.