scv057
commented
4 years ago 全都写在这里啦。收获很大。
Open vianvio opened 4 years ago
vianvio
commented
4 years ago 全都写在这里啦。收获很大。
实在是太牛了，整理的好全面。 最后一题本来想考察一下第3题答案里提到的globalCompositeOperation用法的，不过看到css那个做法，思路真的也是很巧妙呢。
scv057
commented
4 years ago 在前端开发中，当涉及到绘制和动画的时候，我们经常看大一个叫贝塞尔曲线的东西，那么这个东西到底是什么呢？今天我就来重新整理一下。
在这里，首先我们先了解一下它的历史：
贝塞尔曲线依据的最原始的数学公式，是在1912年在数学界广为人知的伯恩斯坦多项式。简单理解，伯恩斯坦多项式可以用来证明，在[ a, b ] 区间上所有的连续函数都可以用多项式来逼近，并且收敛性很强，也就是一致收敛。再简单点，就是一个连续函数，你可以将它写成若干个伯恩斯坦多项式相加的形式，并且，随着 n→∞，这个多项式将一致收敛到原函数，这个就是伯恩斯坦斯的逼近性质。
时光荏苒岁月如梭，镜头切换到了1959年。当时就职于雪铁龙的法国数学家 Paul de Casteljau 开始对伯恩斯坦多项式进行了图形化的尝试，并且提供了一种数值稳定的德卡斯特里奥（de Casteljau） 算法。（多数理论公式是建立在大量且系统的数学建模基础之上研究的规律性成果）根据这个算法，就可以实现 通过很少的控制点，去生成复杂的平滑曲线，也就是贝塞尔曲线。
但贝塞尔曲线的声名大噪，不得不提到1962年就职于雷诺的法国工程师皮埃尔·贝塞尔（Pierre Bézier），他使用这种方法来辅助汽车的车体工业设计（最早计算机的诞生则是为了帮助美国海军绘制弹道图），并且广泛宣传（典型的理论联系实际并获得成功的示例），因此大家称为贝塞尔曲线 。
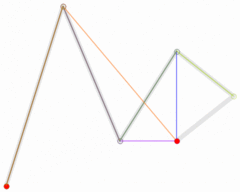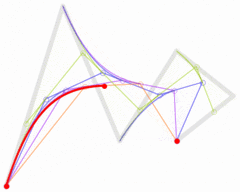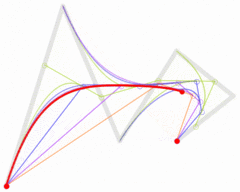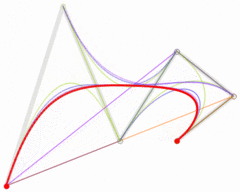
到这里还是看不懂，没关系，我们以二次贝塞尔曲线为例，来研究一下它的几何意义，先给出曲线方程如下: $$ B(t) = (1-t)^2 P0 + 2t(1-t) P1 + t^2 * P2,t∈[0,1] $$ 我们可以通过这样的步骤来绘制一条曲线：
0-1的t值P0和P1计算出点Q0，Q0在P0 P1连成的直线上，并且length( P0, Q0 ) = length( P0, P1 ) * tP1和P2计算出Q1，使得length( P1, Q1 ) = length( P1, P2 ) * tQ1和Q2计算出B，使得length( Q0, Q1 ) = length( Q0, B ) * t。B就为当前曲线上的点有了曲线方程，我们直接代入具体的t值就能算出点B了。
如果将t的值从0过渡到1，不断计算点B，就可以得到一条二次贝塞尔曲线：
同理，我们贴一下三次贝塞尔曲线的绘制过程
四次贝塞尔曲线
五次贝塞尔曲线
所以当贝塞尔曲线在二维平面中就是一条曲线，通过对应的方程，传入起始点，控制点与结束点，我们就可以计算出整条曲线。
那么在动画中，贝塞尔曲线又起到了什么样的作用呢？简单讲就是。通过贝塞尔曲线控制动画的进度，达到一种渐变的效果，不让动画太过突兀。
这个时候我们就要把坐标系重新理解一下了，从原先的用于描述点的位置的坐标系，变成，时间与进度之间的关系。
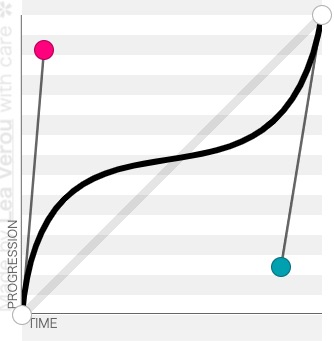
我们把时间与进度也转换为相对值，这样起始点就是(0,0)终止点就是(1,1),t∈[0,1]。
attention！！！！
需要注意的是这里的时间t与上文曲线方程里面的t不是同一个，上文曲线方程里的t是点与点之间的一个百分比，上文真正的时间是，通过方程计算出来的x轴。
接下来用T来表示时间。
接下来我们要解决的就是一个问题，我们如何通过时间T计算出方程里面的t，从而得到对应的p。
这里给出几种思路：
分片迭代
将t分为n等分，对于每个t计算，如果与时间T值处于一定误差范围之内，即取这个B(t)值为结果。
分片迭代的优化
在上面的基础上，先粗略逼近一次，当逼近了的时候继续分片逼近一次，提高精度。
二分法
用二分法不断逼近，当误差范围小于一定值的时候，即认定这个B(t)为结果。
以上几种方法，在单调递增的情况下都是可行的，但如果曲线并非单调递增，那事情就麻烦了。
最后我找到了终极方法：
这样我们就得到求t的方程了，解方程就完事了。
求出t再带入一下方程，我们就可以求出p了。最终得到p = f(T);T∈[0,1]。
代码我直接抄的:
function generate(p1x, p1y, p2x, p2y) {
const ZERO_LIMIT = 1e-6;
const ax = 3 * p1x - 3 * p2x + 1;
const bx = 3 * p2x - 6 * p1x;
const cx = 3 * p1x;
const ay = 3 * p1y - 3 * p2y + 1;
const by = 3 * p2y - 6 * p1y;
const cy = 3 * p1y;
function sampleCurveDerivativeX(t) {
return (3 * ax * t + 2 * bx) * t + cx;
}
function sampleCurveX(t) {
return ((ax * t + bx) * t + cx) * t;
}
function sampleCurveY(t) {
return ((ay * t + by) * t + cy) * t;
}
function solveCurveX(x) {
var t2 = x;
var derivative;
var x2;
// https://trac.webkit.org/browser/trunk/Source/WebCore/platform/animation // First try a few iterations of Newton's method -- normally very fast.
// http://en.wikipedia.org/wiki/Newton's_method
for (let i = 0; i < 8; i++) {
// f(t)-x=0
x2 = sampleCurveX(t2) - x;
if (Math.abs(x2) < ZERO_LIMIT) {
return t2;
}
derivative = sampleCurveDerivativeX(t2); // == 0, failure
/* istanbul ignore if */
if (Math.abs(derivative) < ZERO_LIMIT) {
break;
}
t2 -= x2 / derivative;
}
// Fall back to the bisection method for reliability. // bisection
// http://en.wikipedia.org/wiki/Bisection_method
var t1 = 1;
/* istanbul ignore next */
var t0 = 0;
/* istanbul ignore next */
t2 = x;
/* istanbul ignore next */
while (t1 > t0) {
x2 = sampleCurveX(t2) - x;
if (Math.abs(x2) < ZERO_LIMIT) {
return t2;
}
if (x2 > 0) {
t1 = t2;
} else {
t0 = t2;
}
t2 = (t1 + t0) / 2;
// Failure
return t2;
}
}
function solve(x) {
return sampleCurveY(solveCurveX(x));
}
return solve;
}看完这些，应该对贝塞尔曲线没什么疑问了吧。
问题列表：