Rules:
- Keep all devices in silent mode.
- Don't eat/drink on my bed, sitting/lying is ok.
- Don't leave any trash on the floor. (I always have to clean my house after the seminar/workshop)
- On time: starting time, researching time and discussing time
- Share all your knowledge
- Don't disturb presenters/discussion





Informations:
Contents:
Details:
Arrays/Strings
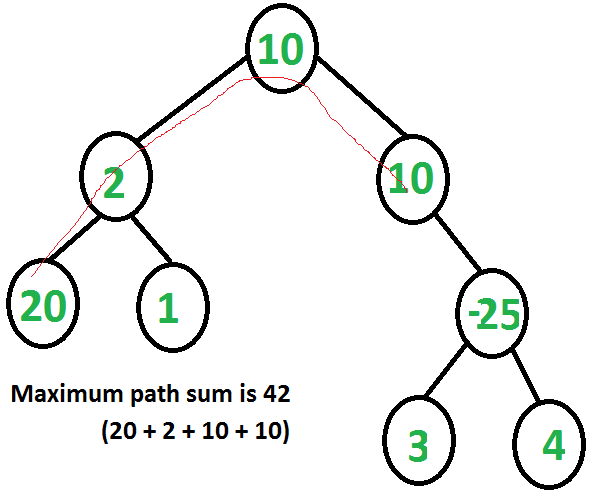
Trees
Prefix Sums
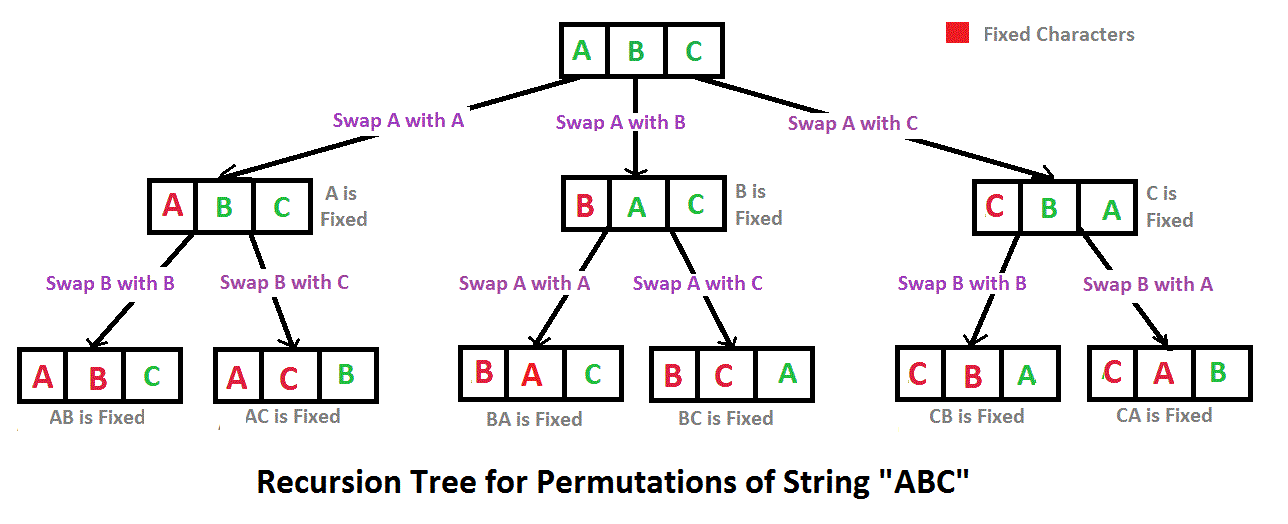
Backtracking