[css-easing-2] Complex easing/timing functions

[rachelnabors]

In light of the Webkit team's implementation of spring(), it's apparent we need to attend to the issue of complex timing functions sooner rather than later.

The problem

Designers often need more advanced timing functions than can be described with cubic-beziers. They are not limited to spring functions, either. A common problem is there is no effective way to export a timing graph from Adobe After Effects to a timing function that could be used with CSS or with the Web Animations API. Currently designers have to hack together individual timing functions using CSS animation keyframes, which is impossible to do by hand in all but the most trifling instances.

spring() is just a bandaid.

The solution

We need a format to write functions like spring() in, one that we can export to from software like AfterEffects and prototyping tools that have yet to be built.

I am not in a position to propose the technical specifications of this solution. But there are people who have that knowledge. I have invited them (@visiblecode) to share their proposals below.

[birtles]

Moving this to [css-timing-2] since I believe that is where we will end up addressing this.

[AmeliaBR]

previously proposed to www-style by @AmeliaBR.

I'd kind of forgotten about that. I'd definitely forgotten that I'd made nice figures to go with it. It would probably be helpful if they were copied over here. Pulling out the key points from my August 2015 proposal here, with some updated links.

---

Make the definition of cubic Bézier curves:

A cubic Bézier curve is defined by a series of control points, P0 through Pn (see [the figure] for an example where n=4). P0 and Pn are always set to (0,0) and (1,1), respectively. The parameters to the easing function are used to specify the values for points P1 to Pn-1. These can be set to preset values using the keywords listed below, or can be set to specific values using the cubic-bezier() function. In the cubic-bezier() function, each point Pi is specified by both an X and Y value.

Then farther down, the syntax and definition of the cubic-bezier function is replaced as follows:

 cubic-bezier([<number>, <number>]*)

Specifies a cubic-polybezier curve. Each pair of values specifies a point Pi in the form x1,y1; an odd-numbered sequence of values is invalid. All x values must be in the range [0, 1] and each x value must be equal to or greater than the previous; otherwise, the definition is invalid. The y values are unrestricted. The series of points is converted to a series of connected cubic Bézier curve segments by grouping into sets of three: two control points followed by a vertex point. If the number of points (plus the implicit 1,1 end point) is not a multiple of three, the sequence is padded with the point 1,1 to create complete cubic Bézier segments.

For example,

• A cubic-bezier function with no parameters is equal to cubic-bezier(1,1, 1,1), which is essentially a linear timing function.
• The ease-in function could also be written as cubic-bezier(0.42,0).

• A multiple bounce transition could be written as follows, resulting in the curve visualized in [Figure]:

   cubic-bezier(0.25,0.25, 0.25,0.75, 0.3,1,
                0.5,0.5, 0.6,0.5, 0.7,1,
                0.85,0.8 0.9,0.8)

  

Finally, a new function could be added to make it easier to make smooth curves:

smooth-cubic-bezier([, ]*) Specifies a cubic-polybezier curve with automatically-calculated smooth connections between segments. Each pair of values specifies a point Pi in the form (x1, y1); an odd-numbered sequence of values is invalid. All x values must be in the range [0, 1], each x value must be equal to or greater than the previous; otherwise, the definition is invalid. The y values are unrestricted.

If there are 1 or 2 pairs of values provided, the result is the same as for the cubic-bezier function. For 3 or more points, an implicit control point is inserted after every vertex point, that is equal to that vertex point plus the vector from the previous control point to that vector point. The remaining explicit points therefore alternate between control points and vertex points. Again, the sequence of points is padded with 1,1 if necessary to make complete cubic Bézier segments.

For example, the following two functions specify the same curve:

smooth-cubic-bezier(0,0.75, 0,1, 0.5,0.5)
cubic-bezier(0,0.75, 0,1, 0.5,0.5, 1,0, 1,1)

Both result in the curve visualized in [Figure]

A first approximation at the figures are attached; if you want to play around quickly, you can also fork from https://jsfiddle.net/L1o71c1c/1/ Or, you know, write a script to generate the SVG markup automatically from a function specification.

Things to discuss:

Given these definitions, should new pre-defined functions be introduced to represent bounce/elastic timing functions in popular JS libraries?

Is the restriction on x values appropriate? We need to ensure that the final curve is a proper function, with each x value having a single corresponding y value. Forcing vertex and control points to be in sorted x order should ensure this, but may be overly restrictive.

It is nonetheless possible to draw a completely vertical arc segment with the current wording. We could address this by adding another restriction (the x values for vertex points must be strictly greater, not just greater or equal to) or we could add an interpretation rule (apply the maximum value, consistent with how the steps function works).

Are the commas between every number in the cubic-bezier function necessary? Do current implementations enforce that syntax? Compare with (a) the Shapes spec which requires commas between points in a polygon, but does not allow them between x y pairs, and (b) SVG syntax, which allows commas and whitespace interchangeably, so many people with mathematical background use commas to join x y pairs and whitespace to separate them, like x1,y1 x2,y2.

[Note that there were comments on the proposal at the time from Brian Birtles, including a link to an even older proposal, that I'll copy into a separate comment to get everything in one place.]

[AmeliaBR]

Proposal for "Stacked Timing Functions" from (I think) a face-to-face breakout session in May 2015, as sent to the fx mailing list in June 2015 by @birtles.

---

STACKED TIMING FUNCTIONS

• Stacked timing functions would allow you to emulate the effect of nested groups.
• However, Brian points out that chained timing functions have the same ability to emulate arbitrary easings, and are also more accessible and more widely applicable - e.g. to produce spring-like easings.

We worked on a syntax for chained timing functions and came up with:

easing: [ tf? point? ]?

Concretely, easings look like

easing: cubic-bezier(a,b,c,d) (x, y) cubic-bezier(e,f,g,h) (x2,y2) ...

You can leave out the points (they're evenly distributed between provided points, where easings always start at (0,0) and end at (1,1).

You can leave out the timing functions (in which case they'll default to linear).

cubic-bezier parameters are always in global (0,0,1,1)-space. This means that you can accidentally provide erroneous easings, e.g.:

easing: cubic-bezier(0.2, 0.8, 0.6, 0.6) (0.5, 0.3) cubic-bezier( 0.6, 0.9, 0.7, 1.0)

Here the first point has an x coordinate that is less than the second x control point of the first bezier (0.5 < 0.6). Concretely, an easing is OK as long as all of the x coordinates (specified and inferred) are in nondescending== increasing order.

So this is incorrect too, although it's hard to see why:

easing: cubic-bezier(0.2, 0.8, 0.6, 0.6) cubic-bezier( 0.6, 0.9, 0.7, 1.0)

becomes:

easing: cubic-bezier(0.2, 0.8, 0.6, 0.6) (0.5,0.5) cubic-bezier( 0.6, 0.9, 0.7, 1.0)

(because that's what easing: linear linear would do)

We could instead infer point x coordinates to be evenly spaced between adjacent specified x coordinates, which would mean that the above would be equivalent to

easing: cubic-bezier(0.2, 0.8, 0.6, 0.6) (0.6,0.5) cubic-bezier( 0.6, 0.9, 0.7, 1.0)

which is actually fine. But if we're doing that, should we do the same thing for the y coordinate?

easing: cubic-bezier(0.2, 0.8, 0.6, 0.6) (0.6,0.75) cubic-bezier( 0.6, 0.9, 0.7, 1.0)

Google to polyfill this. If it's good then we'll add something to L2.

[argyleink]

moving comments from #3838 to here. looks like what I'd specified and more has been covered in this thread, but I'll share what I'd said anyway.

Why

Physics aren't likely to land any time soon to help folks with spring, bounce or cliff effects, and there's big demand for these engaging and lifelike animation tactics. Due to lacking phsyics, folks bring in javascript animation libraries to do the work, or visit websites that generate 100s of keyframes, or just flat out abuse the cubic-bezier() function. JS libraries and cubic-bezier() abuse being the most common, since it's the easiest.

Most of these workarounds result in difficult to manage, rigid or uncanny animations that don't make the web look very great at animation.

Examples

cubic-bezier() https://codepen.io/AdrienBachmann/pen/VYVvGo

JS library (34kb) https://codepen.io/rossorthwein/pen/XorVVV

Proposal

I think we could pacify the need for physics by adding the ability for cubic-bezier() to take more points. Extend cubic-bezier() to chain/concat points together.

Current

Proposed Where we currently have 2 pairs passed into cubic-bezier(), we allow passing additional pairs so more points could be created.

Explode out: source

.animated-layer {
  transition: .2s cubic-bezier(.17,.67,.83,.67,.2,.02,.73,.59, ...);
}

[argyleink]

I'm feeling partial to @AmeliaBR's proposal of smooth-cubic-bezier() as well as adding additional pre-defined functions for things like bounce and elasticity. Cool work! It would be nice to get rid of the commas as well, good call.

[AmeliaBR]

@Lange, that is helpful.

What would also be helpful is a write-up of what values / options are supported (or not) in the major animation software that support complex custom easing curves. Anyone have good resources for that?

Looking at the Adobe help pages for After Effects, it looks like the complex easing can be a mix of smooth or sharp changes, or even steps.

So I'm now starting to doubt whether it is enough to swap between smooth and full beziers for the entire sequence. Maybe it make more sense to focus on chaining arbitrary segments. Making a syntax easy to write by hand is good. But it's probably more important to ensure that it can accurately represent easings that are already being used in design tools.

I like @vidhill's suggestion of trying to define the easing using a syntax that defines the progress as a direct function of time, instead of a syntax that defines an arbitrary 2D curve and then tries to constrain it to only having one progress value for each time point. But the question again is: can existing software export to the syntax without loosing information?

[SebastianZ]

As @visiblecode mentioned earlier, we could simply reuse the path() function currently defined in the Motion Path Module and referring to SVG paths.

That allows combinations of straight lines, quadratic and cubic Beziérs, gaps, and more, in short, should cover all use cases and is consistent to what we already have.

Btw., the timing functions were generalized to also cover color gradients and therefore were renamed to "easing functions". I assume, everything discussed here also applies to gradients, so, maybe someone could rename the summary of this issue accordingly?

Sebastian

[AmeliaBR]

@SebastianZ Path syntax is certainly the most expressive, but it requires extra work to calculate a y-value (interpolated value) at a given x value (time progress or position). And there is no guarantee that you'd get a single y value for any x value.

And yes, we are now talking about generic interpolation functions (although the use cases here all seem to be animation), so I've updated the title to refer to the current name of the spec.

[SebastianZ]

... it requires extra work to calculate a y-value (interpolated value) at a given x value (time progress or position).

Can you please elaborate on that? I don't see why that's work than multiple Beziérs.

And there is no guarantee that you'd get a single y value for any x value.

Right, same issue for Beziérs.

I see two solutions for this problem:

1. Invalidate those paths or Beziérs as you mentioned earlier.
2. Clamp the x coordinate so that the path always increases in x direction. This possibly manipulates the path but makes all paths or Beziérs valid.

Visualisation for the latter:

Input path:

Normalized path:

Sebastian

[visiblecode]

That sort of normalization is pretty rough to pull off in a robust/understandable/easy to implement way.

The big issue we're up against here is that cubic beziers (and SVG paths) aren't really suited for defining easing functions, because they treat x and y independently.

This is good for drawing 2d shapes that are supposed to be able to overlap themselves in arbitrary ways. But for reasons that are pretty obvious above this is super awkward for applications where y is supposed to depend on x, like for easing functions.

Honestly the ideal tool for this is something like a cubic hermite spline. Apart from being about as simple as you can get from an implementation perspective, they're friendlier to hand authoring than beziers are going to be. You'd just need to supplement them with a way to indicate instantaneous jumps in position/speed.

[visiblecode]

Let's look at that in practical terms. To define a cubic hermite spline, you just need a list of (x, y, y') triples.

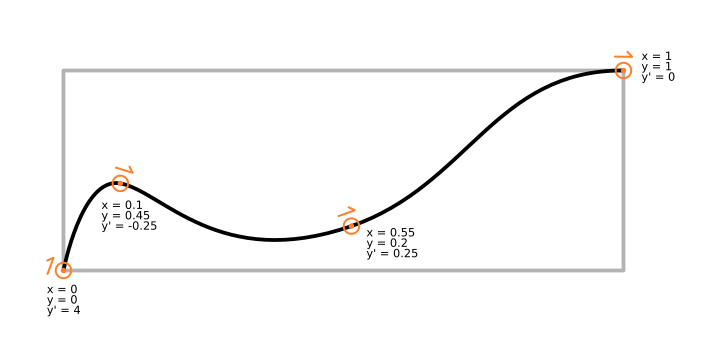
In this context, x would be time, y position, and y' speed. Which should make some intuitive sense from an animation point of view.

[visiblecode]

Right there, that's enough to do most any kind of motion, including springy animations etc. The missing piece is animations where speed or position change abruptly.

So, for the impact point in bounce animations you have to be able to give the incoming and outgoing speed separately.

Animations with jumps in position are similar-ish, except you also need to say which of the incoming or outgoing position gets used when the time is exactly x.

So, without getting too much into syntax, this means you might have a choice of four keyframe/control point "types" for easing splines:

• smooth - (x, y, y')
• sudden speed change - (x, y, y'_in, y'_out)
• sudden position change, use incoming position - (x, y_in, y'_in, y_out, y'_out)
• sudden position change, use outgoing position - (x, y_in, y'_in, y_out, y'_out)

Seems decent for hand-authoring, and it's also general enough to support export from most animation software, either exactly or as an extremely close approximation.

[visiblecode]

Also worth adding that segments of cubic splines are easy to convert into Bernstein form, so implementors can re-use code they already have around for evaluating Beziers.

[tabatkins]

Note that step easings have already made a decision of whether the moment of transition uses prev or next value: they use the next value. So presumably we'd be consistent there, as the use-case for making it controllable seems extremely minimal - you'd only see the difference if you purposely advanced a paused animation to exactly that progress %.

---

Overall, uh, that sounds like a pretty good idea, and the fact that the curve is automatically c1-continuous is nice (unless you purposely drop to c0- or non-continuous by providing additional arguments). I like the physicality of being able to provide a velocity directly, which enables realistic-looking bounces really easily by just inverting the y velocity, like your example shows. (Versus chained beziers, which require much more guess-and-checking to get a realistic-looking bounce.)

[visiblecode]

I think I can sweeten the pot a bit more for hand-authoring. Let's say there's also an auto option for velocity that picks a velocity for you.

For a smooth node with neighbors on both sides, auto would mean choose the velocity to get C2 continuity. That way, if you wanted you could spell out just the times and positions by hand, and automatically get buttery smooth motion.

In the remaining situations, auto would pick the velocity assuming no acceleration. That gives you an easy shorthand for linear motion, which would otherwise be a little clunky to do by hand.

[AmeliaBR]

I do like @visiblecode's proposal for hand-authoring friendliness (especially with an automatic curve fitting option), and for the fact that it directly defines y as a function of x, so doesn't need arbitrary limits or fix-ups.

But hand-authoring is only half of the argument. The other is compatibility with existing tools.

Also worth adding that segments of cubic splines are easy to convert into Bernstein form, so implementors can re-use code they already have around for evaluating Béziers.

Do you have a link to the relevant formulae? Are these exact conversions or approximations?

Ideally, this would become the new "master" syntax, that could represent all the keyword and function-notation easings defined in the current spec. In particular, I'd be interested to know if your definition of "automatic" velocity calculations matched Blender's automatic handles.

But we'd also want to directly represent curves that can be generated in popular animation software, like AfterEffects and Blender, which seem to use a mix of straight lines and cubic curves (with internally-enforced limits on the curves to keep them always increasing in the x direction).

We'd also want to make it possible to convert from software that currently uses path notation, like Greensock. Which, based on my testing with their visualizer, seems to use the rule proposed by @SebastianZ to convert arbitrary paths into functions.

[visiblecode]

My take-away from the couple years I spent on this is:

1. There's too much variation in the way different software represents animation curves to allow for a "master" representation that can seamlessly roundtrip with all of them
2. Some popular ways of specifying animation curves only allow approximate implementations to begin with
3. Where round-tripping the original representation isn't a concern, any animation curve can be converted to cubic splines with good fidelity (sometimes with added control points)

[visiblecode]

brief overview on the math, I can go into more detail on specific things if you want

Every segment of a cubic spline translates to a cubic polynomial. There are a number of ways to represent a cubic polynomial, which are all exactly convertible (within the limits of floating point precision etc.), including:

• the obvious way: ax³ + bx² + cx + d
• Hermite form: starting value, starting tangent, ending tangent, ending value
• Bernstein form: starting value, two control values, ending value

The thing is, Bézier curves are based on Bernstein polynomials (the bezier handles map to the control values). The catch is that a 2D Bézier curve segment consists of two polynomials, one for x and one for y. For drawing curves on screen that's perfect, the two polynomials can be evaluated directly, independently, with all the usual advantages of cubics. Mathematically precise, versatile, and efficient to evaluate.

But, for uses like CSS's cubic-bezier(), you have to solve for the unique root of the x polynomial (with things constrained so there is one), and plug the result into the y polynomial. The root finding part isn't possible to do super efficiently, so in practice what most implementations of cubic-bezier() do is precompute a rough approximation and linearly interpolate over that. It works okay, but there's a big speed/accuracy tradeoff. Probably there's more variation between implementations than people realize, especially in extreme cases.

TBH, in general implementors would probably get better results (both in terms of accuracy and also performance) converting each cubic-bezier() segment to a cubic spline (of ~1-3 segments) rather than trying to approximate cubic-bezier() directly in realtime.

There are a bunch of other animation curve representations which get used as well, NURBS and so on. Some of these superficially resemble Béziers (they have similar handles, etc.), but don't allow exact conversion to/from them.

Blender's smoothing is a bit different to the auto thing I described above (which is based on spline interpolation). Blender's curves can still be approximated by cubic splines but you wouldn't use auto to do it.

[visiblecode]

We'd also want to make it possible to convert from software that currently uses path notation, like Greensock. Which, based on my testing with their visualizer, seems to use the rule proposed by @SebastianZ to convert arbitrary paths into functions.

What Greensock does is discard the parts of the path between where x starts decreasing to where it catches up again. I don't know the details of the implementation, but bezier path intersections tend to have rough edge cases to account for.

Obviously any reasonable easing representation should be able to support export of a "baked" representation (after pruning, etc). But should browsers be expected to implement on-the-fly pruning themselves?

[AmeliaBR]

But should browsers be expected to implement on-the-fly pruning themselves?

If we adopt a system where you can directly use SVG path notation, then yes, I would expect some sort of reasonable error handling like that. So that comment was more of an aside, going back to the discussion of the alternative.

But if we adopt something like the cubic spline syntax, the main question is can a tool like Greensock implement an algorithm to convert (with a reasonable degree of fidelity) their fixed-up path into the standard notation.

[flackr]

I have on occasion found myself wanting to supply a formula to express timing functions for example when I wanted to perfectly invert another timing function to implement an accelerated expanding reveal animation. We ended up approximating this inverse scale with a generated linear animation with lots of keyframes but it could have been expressed as a single formula. Could supplying a formula solve some of these other express-ability use cases as well?

[visiblecode]

@AmeliaBR wrote:

If we adopt a system where you can directly use SVG path notation, then yes, I would expect some sort of reasonable error handling like that.

Fair!

But if we adopt something like the cubic spline syntax, the main question is can a tool like Greensock implement an algorithm to convert (with a reasonable degree of fidelity) their fixed-up path into the standard notation.

Yes.

@flackr wrote:

We ended up approximating this inverse scale with a generated linear animation with lots of keyframes but it could have been expressed as a single formula. Could supplying a formula solve some of these other express-ability use cases as well?

Mostly no. (Though having calc() available as an option for easing functions is kind of tempting anyhow.) The problem is many functions don't have a (practical) formula representation -- including functions that result from cubic-bezier()'s (ab)use of Béziers!

The simplest general-purpose solution for representing arbitrary functions (including ones that can't be expressed as formulas) is to use a piecewise polynomial approximation.

Piecewise linear (degree 1) is one version of that, but as you discovered needs a lot of keyframes.

Piecewise cubic (degree 3), which we're discussing here, is kind of a sweet spot where you don't need that many extra keyframes, but it's still cheap to evaluate and can't go uncontrollably wiggly as can be a problem for degree >= 4.

[visiblecode]

But if we adopt something like the cubic spline syntax, the main question is can a tool like Greensock implement an algorithm to convert (with a reasonable degree of fidelity) their fixed-up path into the standard notation.

Apparently this isn't a requirement for Greensock. I chatted with the Greensock author about this today, and the way he explained it was instead of generating CSS and delegating to the browser, Greensock always drives animations from JavaScript.

Greensock has its own internal representation for easings that's optimized for efficiency vs perfect accuracy, and it always converts everything (CSS-style easings, SVG path easings, etc) to that internal representation before animating.

[visiblecode]

Probably exporting animations from Blender is a better model use case.

[visiblecode]

I had a thought this week -- knots in a spline are a lot like stops in a gradient, just with value+slope instead of colors.

...what if the syntax for splines worked like the syntax for gradients?

animation-timing-function: cubic-spline(<position> <speed> <time%>, ...);

So for example:

animation-timing-function: cubic-spline(0 0 0%, 0.1 auto 25%, 0.5 auto 50%, 0.9 auto 75%, 1 0 100%);

It probably makes sense to support some shorthands.

To start with, using the rules for gradient stops, if you just want equal spacing you can leave off the knot times/percentages:

animation-timing-function: cubic-spline(0 0, 0.1 auto, 0.5 auto, 0.9 auto, 1 0);

It'd probably also make sense to make speed optional (defaulting to auto):

animation-timing-function: cubic-spline(0 0, 0.1, 0.5, 0.9, 1 0);

(Both of these give the same result as the original above.)

That feels pretty nice.

If we go with the same rules as for gradients, you can create abrupt changes by doubling up knots:

animation-timing-function: cubic-spline(0, 1 50%, 1 50%, 0);

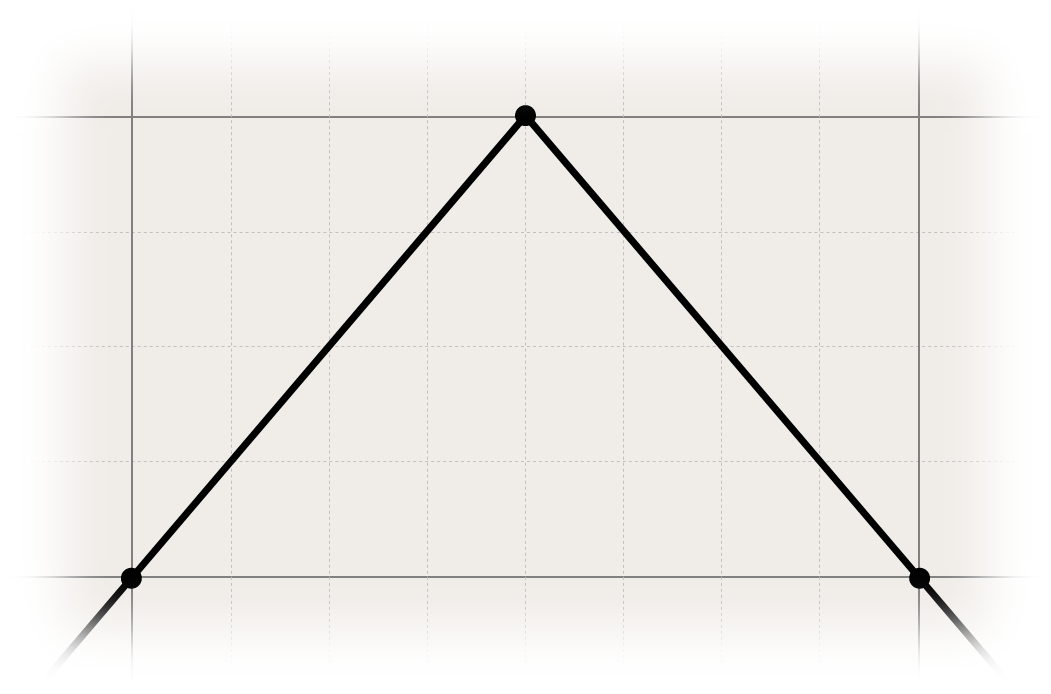
animation-timing-function: cubic-spline(0.5, 1 50%, 0 50%, 0.5);

animation-timing-function: cubic-spline(1 0, 0 -3 50%, 0 3 50%, 1 0);

EBNF syntax for this idea might look something like:

<cubic-spline-easing-function> = cubic-spline( <cubic-spline-knot-list> )

<cubic-spline-knot-list> = <cubic-spline-knot> [, <cubic-spline-knot># ]?
<cubic-spline-knot> = <cubic-spline-knot-position> <cubic-spline-knot-speed>? <cubic-spline-knot-time>?

<cubic-spline-knot-position> = <number>
<cubic-spline-knot-speed> = auto | <number>
<cubic-spline-knot-time> = <percentage>

[visiblecode]

Also, here's a bounce easing I prepared by hand:

animation-timing-function: cubic-spline(0 0, 1 50%, 1 50%, 0.5, 1 75%, 1 75%, 0.75, 1 87.5%, 1 87.5%, 0.875, 1 93.75%, 1 93.75%, 0.9375, 1 96.8%, 1 96.8%, 0.968, 1 98.4%, 1 98.4%, 1);

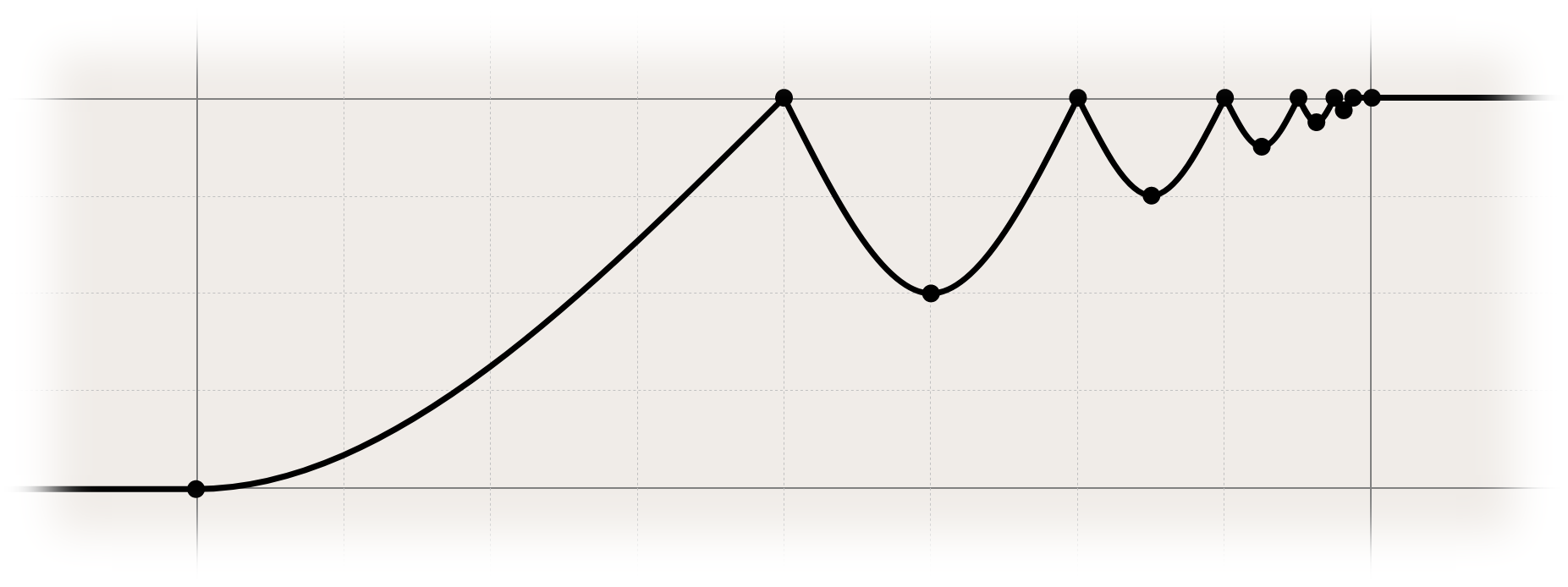
Edit: Also, a handmade spring easing.

animation-timing-function: cubic-spline(0 0, 1.5 0 50%, 0.75 0 75%, 1.125 0 87.5%, 0.9375 0 93.75%, 1.031 0 96.8%, 0.984 0 98.4%, 1 0);

[birtles]

Those are neat diagrams and the effects you've produced look great. They seem to cover the different use cases well.

As someone who is not very familiar with gradients (I need to look it up every time) I don't find the parallel with gradient syntax particularly helpful. In particular, putting the "y" value (<cubic-spline-knot-position>) before the "x" offset (<cubic-spline-knot-time>) feels back-to-front compared to how I'm used to thinking with regards to keyframe offsets. However, that may be just me, and given that these easing functions may be used with gradients, aligning the syntax probably makes sense.

Currently all easing functions go from (0,0) to (1,1). I'm unsure if we should break that invariant or not (as this syntax currently allows). I seem to recall it had unfortunate implications in the realm of GroupEffects (where timing functions are effectively layered on top of one another) but perhaps it's ok.

[visiblecode]

Since it's already allowed in a more limited way, letting the dependent variable (progress) to go outside the 0..1 range shouldn't be much of a problem.

For the independent variable (time), though -- I'd imagined we'd just use the section of the timing function between 0 and 100%, regardless of where the first/final knots are, extrapolating past the end knots with straight lines if necessary.

animation-timing-function: cubic-spline(0 0 30%, 1 0 66%);

[visiblecode]

I'm not super attached to the gradient syntax, it just seemed like a nice opportunity for syntactic uniformity with the rest of CSS.

[birtles]

Since it's already allowed in a more limited way, letting the dependent variable (progress) to go outside the 0..1 range shouldn't be much of a problem.

Right, that part is fine.

For the independent variable (time), though -- I'd imagined we'd just use the section of the timing function between 0 and 100%, regardless of where the first/final knots are, extrapolating past the end knots with straight lines if necessary.

What I'm more concerned about is when f(0) != 0 or f(1) != 1. There certainly used to be places where we assumed that. With step-start you can already have f(0) != 0 but only when the "before flag" is false.

I recall that in the past that invariant proved useful but perhaps it's fine now. (It may have been when we were trying to chain timing functions together, or when we were trying to invert them in order to work out when to dispatch events -- but we don't do either of those things anymore).

[visiblecode]

What I'm more concerned about is when f(0) != 0 or f(1) != 1. There certainly used to be places where we assumed that. With step-start you can already have f(0) != 0 but only when the "before flag" is false.

I recall that in the past that invariant proved useful but perhaps it's fine now. (It may have been when we were trying to chain timing functions together, or when we were trying to invert them in order to work out when to dispatch events -- but we don't do either of those things anymore).

It'd be worth grounding out on whether there are any lingering issues with lifting this restriction, for both Gecko and WebKit. As long as the restriction is in place, there's a whole family of complex animations left that can't be expressed except the "long way", with multiple keyframes.

For example:

Without the requirement that f(0) == 0 and f(1) == 1, this animation could be expressed the same way as other complex animations (using the gradient-style strawman syntax):

@keyframes bouncy {
    0% {
        transform: translate(0px);
        animation-timing-function: cubic-spline(0, 1, 0 33%, 0 33%, 0.33, 0 66%, 0 66%, 0.11, 0);
    }
    100% {
        transform: translate(90px);
    }
}

But, if the restriction were in force, for certain animations like this one you'd be forced to fall back to something like:

@keyframes bouncy {
    0% {
        transform: translate(0px);
        animation-timing-function: cubic-spline(0, 1 0);
    }
    16% {
        transform: translate(90px);
        animation-timing-function: cubic-spline(0 0, 1);
    }
    33% {
        transform: translate(0px);
        animation-timing-function: cubic-spline(0, 1 0);
    }
    49% {
        transform: translate(30px);
        animation-timing-function: cubic-spline(0 0, 1);
    }
    66% {
        transform: translate(0px);
        animation-timing-function: cubic-spline(0, 1 0);
    }
    82% {
        transform: translate(10px);
        animation-timing-function: cubic-spline(0 0, 1);
    }
    100% {
        transform: translate(0px);
    }
}

(There's still a somewhat shorter way to write this, which I'll leave as an exercise for the reader because it requires a re-parameterization that's annoying to do by hand.)

[AmeliaBR]

@visiblecode How would you handle transitions, or filled animations, if the easing function doesn't reach the the target “end” value at the end time? Would the value jump suddenly to match?

[visiblecode]

@visiblecode How would you handle transitions, or filled animations, if the easing function doesn't reach the the target “end” value at the end time? Would the value jump suddenly to match?

Yes, similar to the current situation with some step easings.

Edit: For fills, I guess it might make sense to hold the last computed value to make animations like the above possible. Which would be different to the behavior for step.

[birtles]

Edit: For fills, I guess it might make sense to hold the last computed value to make animations like the above possible. Which would be different to the behavior for step.

Right, for fills it is already possible to fill at the mid-point of an interval by using animation-iteration-count: 0.5 for example.

[visiblecode]

That's an interesting point. I think we can get away without having any special fill behavior.

For use cases involving complex exported animations, multiple intermediate keyframes would be the norm anyhow.

[css-meeting-bot]

The CSS Working Group just discussed easing timing functions.

The full IRC log of that discussion

<fremy> Topic: easing timing functions
<astearns> github: https://github.com/w3c/csswg-drafts/issues/229
<fremy> AmeliaBR: this is another old issue, that had a lot of discussion for a while, but every so often somebody finds it again, and revives the issue
<fremy> AmeliaBR: the issue is that all the easing functions are only continuous curves
<fremy> AmeliaBR: you can use strong coefficients to create a slight overshoot, but that doesn't allow rebounds
<fremy> AmeliaBR: so the request is to have more complex functions
<fremy> AmeliaBR: most animation software have ways to create those functions, but now they can't be exported to css
<hober> q+
<fremy> AmeliaBR: and they have to be exported to huge keyframe sequences which are difficult to maintain and understand
<hober> https://lists.w3.org/Archives/Public/www-style/2016Jun/0181.html
<astearns> https://github.com/w3c/csswg-drafts/issues/229#issuecomment-492367598
<fremy> AmeliaBR: there is a proposal to use cubic bezier but it allows too much for what we want
<fremy> AmeliaBR: there is also a more recent proposal, and I happen to like it
<dbaron> cubic beziers as defined currently are well-defined functions since we give only 2 of the 4 control points and the x values are constrained to [0,1]
<fremy> AmeliaBR: but there is also the option of using the cubic bezier syntax and let the browser fix that up if the function isn't pure
<astearns> ack hober
<fremy> AmeliaBR: so our first question, what should we do first, get a great syntax or extend the type of syntax we have now
<hober> spring(mass stiffness damping initialVelocity)
<fremy> hober: we think this is a good idea
<fremy> hober: we like this syntax, and we are all for it
<fremy> astearns: any other comment?
<fremy> heycam: what's the unit that this proposal used?
<fremy> heycam: css values should have the answer
<flackr> q+
<fremy> astearns: dbaron pointed out on irc that cubic-bezier can work as functions
<astearns> ack flackr
<fremy> AmeliaBR: yes because we remove some parameters, but as you try to add expressivity, it's difficult to maintain that
<majidvp> q+
<astearns> ack majidvp
<fremy> majidvp: one thing I like about this idea, it's possible to approximate a spring using the proposal, which is great because other we have to specify ourselves all the types of bounds we want, but authors will still want more
<hober> s/we think this is a good idea/dean proposed a spring timing function a few years ago. we're supportive of having such a thing./
<fremy> AmeliaBR: yes, if we have a generic expression syntax that handles many things, we can get spring to be an alias to that
<hober> s/we like this syntax, and we are all for it//
<argyle> 😍
<fremy> astearns: I don't see much desire to discuss the precise syntax, but there is some interest
<fremy> fantasai: should we add somebody to edit the spec?
<fremy> astearns: but I don't see enough interest to add this to a spec
<fremy> myles_: AmeliaBR what are you trying to achieve here?
<fremy> AmeliaBR: get agreement that a generic mechanism would be great to add to easing-2
<fremy> myles_: my problem with the generic approach, is that the end result is just complex math, and doesn't explain what the end result should look like
<fremy> myles_: which is why I prefer `spring` because it has clear intent
<fremy> myles_: also, as designer, I think I would draw what I want in a software, as a piece-wise function
<astearns> ack dbaron
<fremy> myles_: and that is not easy to express as a cubic-bezier
<fremy> dbaron: I think adding new things in that space is reasonable, but I think I would want to weight the implementation cost, but in general I'm in favor of adding expessivity in the spec here
<fremy> AmeliaBR: the last proposal has very nice pictures, and seem well accepted
<dbaron> dbaron: nice pictures and few/no equations
<fremy> astearns: one way to make progress is to find the contributor that submitted the various comments, and convince that person to collect them in a spec in wicg
<fremy> AmeliaBR: I'm willing to try to get that to happen, if there are other people interested they are welcome to join me
<majidvp> q+
<fremy> flackr: I'm interested in the space as well, but didn't evaluate
<fremy> flackr: the current proposal
<astearns> ack majidvp
<fremy> flackr: but my attention will be about ease of write, and ease of parse
<fremy> fantasai: and ease-of-read as well
<fremy> flackr: yes
<fremy> majidvp: i would also want to note that if you have an houdini approach, we can allow any js function, then sample it
<fremy> majidvp: previously houdini was a big leap in the space
<fremy> majidvp: but right now, we have a lot of things ready, and this would be easily doable
<fremy> hober: I'm weary of putting off very desirable features to js
<fremy> majidvp: I'm not saying we shouldn't do a declarative approach, but I don't see why both can't be pursued at the same time
<fremy> hober: sure
<fremy> myles_: we are fine with a houdini approach
<fremy> myles_: but that shouldn't prevent us from delivering features that are directly relevant to authors
<hober> s/to js/until houdini is ready/
<myles_> s/we are fine with a houdini approach/the presence of houdini doesn't allow us to stop making good features for our users/
<majidvp> I agree with that sentiment :)
<fremy> AmeliaBR: ok, so the conclusion is that we are going to try to gather a community to make this happen, thanks everyone for the feedback
<fremy> <br /> (after which we would talk about motion-blur)

[visiblecode]

dbaron: nice pictures and few/no equations

I wasn't sure if spelling out the equations would be necessary at this stage. As mentioned upthread, the piecewise curves here are supposed to be Cubic Hermite splines. They are a standard thing and very closely related to Bezier curves.

Hermite splines can be given as a sequence of (t, p, m) triples, corresponding to the knots. In this context those correspond to (time, progress, velocity), with time and progress ranging between 0 and 1, apart from under/overshoot.

(n.b. the strawman CSS syntax from earlier gives t last, and as a percentage, just because it's trying to imitate CSS gradient syntax.)

I'll use t₀ to mean the t from the first knot, t₁ from the second knot, and so on...

For evaluating the curve in between knots, it's probably easiest to convert the segments to Bernstein form. (Bezier curves are made of polynomials in Bernstein form.)

Converting one Hermite segment, between knots n and n+1, to Bernstein form and re-parameterizing for the unit interval:

Δt_n = t_n+1 - t_n

C₀ = p_n C₁ = p_n + m_n Δt_n / 3 C₂ = p_n+1 - m_n+1 Δt_n / 3 C₃ = p_n+1

Evaluating the converted segment for some t, using De Casteljau's algorithm, as is commonly done for Beziers:

lerp(a, b, x) = (1 - x) a + x b

t_unit = (t - t_n) / Δt_n

B₀ = lerp(C₀, C₁, t_unit) B₁ = lerp(C₁, C₂, t_unit) B₂ = lerp(C₂, C₃, t_unit)

A₀ = lerp(B₀, B₁, t_unit) A₁ = lerp(B₁, B₂, t_unit)

result = lerp(A₀, A₁, t_unit)

One non-standard thing is that I'm allowing zero length segments (where t_n == t_n+1) to represent abrupt changes in the curve; these trivial segments shouldn't get evaluated.

When I have a chance, I'll follow up on how to compute unspecified m_n values (missing or auto in the strawman syntax).

[visiblecode]

Missing m_n values (slopes) can be worked out by solving a system of linear equations with an equation per knot.

If a knot's slope is already known, the equation is trivial:

m_n = the slope

Otherwise, assuming:

Δt_n = t_n+1 - t_n Δp_n = p_n+1 - p_n

It's a choice between:

A. m_n = 0 B. 2 m_n / Δt_n + m_n+1 / Δt_n = 3 Δp_n / Δt_n² C. m_n-1 / Δt_n-1 + 2 m_n / Δt_n-1 = 3 Δp_n-1 / Δt_n-1² D. m_n-1 / Δt_n-1 + 2 m_n (1 / Δt_n-1 + 1 / Δt_n) + m_n+1 / Δt_n = 3 * (Δp_n-1 / Δt_n-1² + Δp_n / Δt_n²)

Which equation to use depends on the knot's neighbors:

Previous Knot	Next Knot	Equation
none	none	A
none	same t	A
same t	none	A
none	different t	B
same t	different t	B
different t	none	C
different t	same t	C
different t	different t	D

This choice of equations amounts to doing standard spline interpolation for each unbroken section of curve with unknown slopes.

The tridiagonal matrix algorithm is a good fit for solving the resulting system of equations and is easy to implement.

[AmeliaBR]

Thanks for the equations, @visiblecode !

What did you think about turning this into a WICG proposal? That would have two benefits:

1. People would be able to edit and keep track of the final proposal without reading this entire thread!
2. It would involve you confirming that you're contributing all your intellectual property claims in your proposal under a licence that is compatible with W3C specs.

Myself and @argyleink have said we'd be able to help coordinate & deal with the formatting aspects of the proposal, but we'd need the IP contributions sorted out first.

[visiblecode]

Okay, I'm willing to give it a shot, though it may be a couple weeks before I can get back to you.

[argyleink]

wanted to share for potential reference and relevance https://github.com/lunelson/split-ease

[okikio]

I personally prefer Jake Archibalds @jakearchibald easing-worklet proposal, it seems a little more straight forward, what do you guys think?

[jakearchibald]

I wonder if it'd be even simpler to provide multiple points and just linear interpolate between them. You can produce almost any effect with enough points.

The more complex curves can land later, when folks figure them out.

[okikio]

Krill Vastletov discussed something similar in this article https://www.kirillvasiltsov.com/writing/how-to-create-a-spring-animation-with-web-animation-api/, if so we may not need to even finalize the api and can just start with custom made point easing today.

[jakearchibald]

Yeah, you can hack it with keyframes today, but it'd be nice if it could be could be used within keyframes. Something like linear-easing(0, 0.1, 0.3, 0.6, 0.8, 1) or whatever would be enough.

[flackr]

Yeah, you can hack it with keyframes today, but it'd be nice if it could be could be used within keyframes. Something like linear-easing(0, 0.1, 0.3, 0.6, 0.8, 1) or whatever would be enough.

Agreed, having to calculate interpolated keyframe values can be complicated depending on property values being interpolated and is destructive (i.e. your animation's original keyframes are now lost).

[jakearchibald]

@birtles @grorg @smfr how do you feel about going forward with something like linear-easing(0, 0.1, 0.3, 0.6, 0.8, 1), which defines a set of easing points with linear interpolation in between?

I imagine the definitions of linear-easing could get pretty long, with enough points to look smooth, but now we have custom properties they can be turned into a library.

It still leaves the door open for a curve-based solution like cubic-spline.

[birtles]

@birtles @grorg @smfr how do you feel about going forward with something like linear-easing(0, 0.1, 0.3, 0.6, 0.8, 1), which defines a set of easing points with linear interpolation in between?

I'd be in favour of that. Particularly for a < 1s animation I imagine it wouldn't require too many points to produce a convincing effect.

[jakearchibald]

Here's a little demo to test that https://static-misc-3.glitch.me/linear-easing/.

Cases like bounce are tricky due to sudden changes of direction, but 50 points seems to do well.

[benlesh]

I guess people would need to lean on SASS and LESS even harder to generate these series of points. It seems like something that could be evaluated would be better. Something like calc being the precedent.