Matrix valued coefficients as input to Wilson

[MJKirk]

When matching from a UV theory onto the SMEFT, often one gets pretty simple generic formulas for the SMEFT coefficients. As an example, take this from the wilson paper (bottom of page 9) But actually typing out all the coefficients is tedious and error prone. Again from there, you give the example code 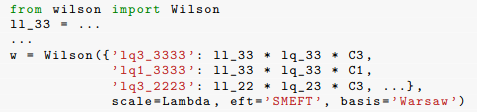If I'm correct, there are actually another 17 coefficients hidden in that "..." that you didn't bother to type out, and of course you have to remember which are the non-redundant ones.

Instead, it's pretty easy to use the following code

# Some example values
 ll_33 = 1
lq_33 = 1
ll_23 = 0.2
lq_23 = -0.1
C1 = -0.05
C3 = 0.02

ll = np.array(((0,0,0),(0,ll_23**2, ll_23), (0, ll_23, ll_33)))
lq = np.array(((0,0,0),(0,lq_23**2, lq_23), (0, lq_23, lq_33)))
Clq1 = C1*np.einsum("ij,kl->ijkl", ll, lq)
Clq3 = C1*np.einsum("ij,kl->ijkl", ll, lq)

to generate all the wilson coefficients (in what should be the basis where coefficients have the same symmetries as the operators). Then you can do

wilson.util.smeftutil.arrays2wcxf_nonred(wilson.smeftutil.add_missing({"lq3": Clq3, "lq1": Clq1}))

to get a dictionary with just the non-redundant coefficients needed to initialise a Wilson instance.

My questions are: 1) Does that combination of functions do the correct thing? I.e. take care of the symmetries correctly etc. I talked to @peterstangl last week and he agreed that there was some internal function that does this, and I believe arrays2wcxf_nonred is what I want, not arrays2wcxf. and 2) Do you think this has wider use, and if so, what about making this an official way to get a Wilson instance? I would say using the numpy summation makes it much easier to see if you have the correct formula, and much less typo prone.

[peterstangl]

Except for a small typo, I think your example should do the correct thing. However, if you want to use redundant arrays as input, you might want to check that they have been actually properly symmetrized. E.g. one could use a function like

from wilson.util import smeftutil

def C_arrays_to_C_wcxf(C_arrays):
    C_wcxf = smeftutil.arrays2wcxf_nonred(smeftutil.add_missing(C_arrays))
    C_arr_sym = smeftutil.wcxf2arrays_symmetrized(C_wcxf)
    for k,v in C_arrays.items():
        if not np.all(C_arr_sym[k] == v):
            raise ValueError(f'Input array "{k}" is not properly symmetrized.')
    return C_wcxf

We could think about including such a function in a Wilson.from_C_arrays class method that would work similar to Wilson.from_wc. We just might have to find a better name :wink:

Another idea would be to check whether the input dictionary contains keys for redundant arrays (i.e. lq1, lq3, etc.) or for non-redundant entries (i.e. lq1_1111, lq1_1112, etc.). Then both options could be accepted as inputs and for the first option one could just call C_arrays_to_C_wcxf internally.

[MJKirk]

Thanks Peter! As a physics point, regarding the symmetry check, assuming I'm taking my expressions from some UV matching, this is just a check against typos right? Matching should give you things with the right symmetries?

For the code, my quick opinion is that a Wilson.from_C_arrays class method would be clearer, as it keeps the standard that Wilson only takes the non-redundant inputs, and that going from arrays is a separate thing that you typically aren't using.

[DavidMStraub]

I agree that correct symmetrization must definitely be checked when allowing non-redundant input. Even if correct matching should give you the correctly symmetrized WCs, it's something to easily get wrong and it would lead to weird and hard to debug errors.

I advise against switching between assuming redundant and non-redundant conventions based on user input. This is prone to lead to unintended behaviour, e.g. in the case of typos. It is much better IMO to have to separate options and fail in both cases if the assumptions are not met.

[MJKirk]

An update from real world testing - the np.all(C_arr_sym[k] == v) check often fails due to tiny numerical errors. I've replaced the check with np.allclose(C_arr_sym[k], v, atol=0) and now things are working.

[MJKirk]

Spoke a little too soon, sometimes I get differences that are relatively big, but absolutely small, e.g. 3e-31 vs 1e-31. Since the rest of the array has much larger values (order 1e-10), I would guess this is just more floating point errors creeping in. So the comparison is not trivial.

[peterstangl]

I'm a bit surprised that you get such big relative differences when going to the non-redundant description and then back to the symmetrized one. Do you get this only in cases where the value is actually zero up to numerical uncertainties? Can you maybe provide an example for which you get such results?

[MJKirk]

No, the example I found was for a non-zero WC (albeit very small, as it suppressed by a bunch of CKM factors and the charm mass). Here's a simplified version of my code

from math import pi
import numpy as np
from wilson.util import smeftutil
from ckmutil.ckm import ckm_tree

xi = np.array((-0.8, 0, 0))
_Vus = 0.2253
_Vub = 0.0041
_Vcb = 0.0421
_delta = 1.14
vckm1 = ckm_tree(_Vus, _Vub, _Vcb, _delta)

vckm2 = np.array(
 ((0.974281, 0.2253, 0.00171214 - 0.0037254j),
  (-0.225172 - 0.000152808j, 0.973409 - 0.0000353365j, 0.0421),
  (0.00781865 - 0.0036264j, -0.0414033 - 0.000838595j, 0.99910))
)

print(np.allclose(vckm1, vckm2, rtol=1e-6))
print(vckm1 / vckm2 - 1)

vckm = vckm2

yudiag = np.diag((0, 1.3/174, 1))
yu = vckm.T.conj() @ yudiag
yubar = yu.conj()

qu1 = ( 3 * np.einsum("i,j,Al,Ak->ijkl", xi, xi, yu, yubar) / (128)
       +1 * np.einsum("A,j,il,Ak->ijkl", xi, xi, yu, yubar) / (192)
       +1 * np.einsum("A,i,Al,jk->ijkl", xi, xi, yu, yubar) / (192)
       -1 * np.einsum("A,A,il,jk->ijkl", xi, xi, yu, yubar) / (96) )

print(qu1[0,0,2,1])

def C_arrays_to_C_wcxf(C_arrays):
    C_wcxf = smeftutil.arrays2wcxf_nonred(smeftutil.add_missing(C_arrays))
    C_arr_sym = smeftutil.wcxf2arrays_symmetrized(C_wcxf)
    for k,v in C_arrays.items():
        # if not np.all(C_arr_sym[k] == v):
        if not np.allclose(C_arr_sym[k], v, atol=0):
            raise ValueError(f'Input array "{k}" is not properly symmetrized.')
    return C_wcxf

try:
    C_arrays_to_C_wcxf({"qu1": qu1})
except ValueError as e:
    print(e)
    C_wcxf = smeftutil.arrays2wcxf_nonred(smeftutil.add_missing({"qu1": qu1}))
    C_arr_sym = smeftutil.wcxf2arrays_symmetrized(C_wcxf)
    for i in range(3):
        for j in range(3):
            for k in range(3):
                for l in range(3):
                    if not np.isclose(qu1[i,j,k,l], C_arr_sym["qu1"][i,j,k,l], atol=0):
                        print((i,j,k,l), qu1[i,j,k,l], C_arr_sym["qu1"][i,j,k,l], qu1[i,j,k,l] / C_arr_sym["qu1"][i,j,k,l])

The only "wrong" element is the C_1132, which I print. With vckm1 (what I was using), you get the factor two I gave earlier. But if you use the other CKM values (which as this code demonstrates are different by tiny factors), then a) you don't get the error but also b) the actual value of C_1132 is larger by a factor 10^10. Which all suggests to me some numerical issues

[MJKirk]

Okay, on further investigation, in this particular case, with only a first gen NP coupling (my xi vector), the analytic expression for C_1132 can be simplified and is exactly zero (through the unitarity of the CKM matrix). So in my above code, the tiny differences between vckm1 (more precise) and vckm2 (less precise) are breaking GIM cancellation. And this somehow ends up affecting the conversion numerics such that the symmetrisation check goes through.