I've added ASERT to my fork of the kyuupichan difficulty test suite. This test suite allows for testing different algorithms with the same random seed (@zawy12, do I remember correctly that your suite uses a different random seed each time?). Unsurprisingly, ASERT performs basically identically to WTEMA on all metrics. The only differences between the two are small enough to be explained by rounding errors.
http://ml.toom.im:8051/ https://github.com/jtoomim/difficulty/blob/comparator/mining.py#L313
Also, here's Mark Lundeberg's paper about ASERT:
http://toom.im/files/da-asert.pdf










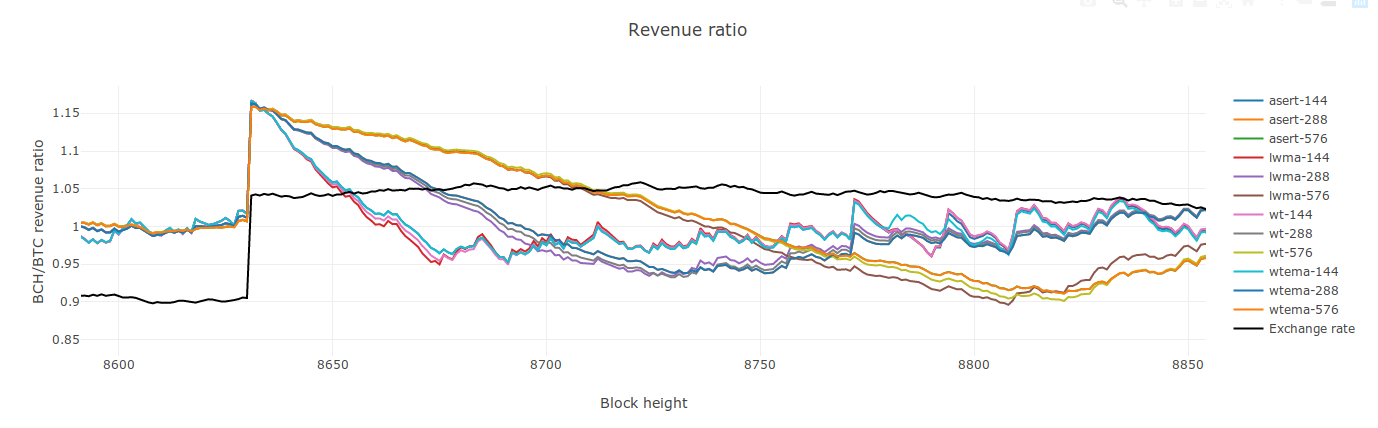
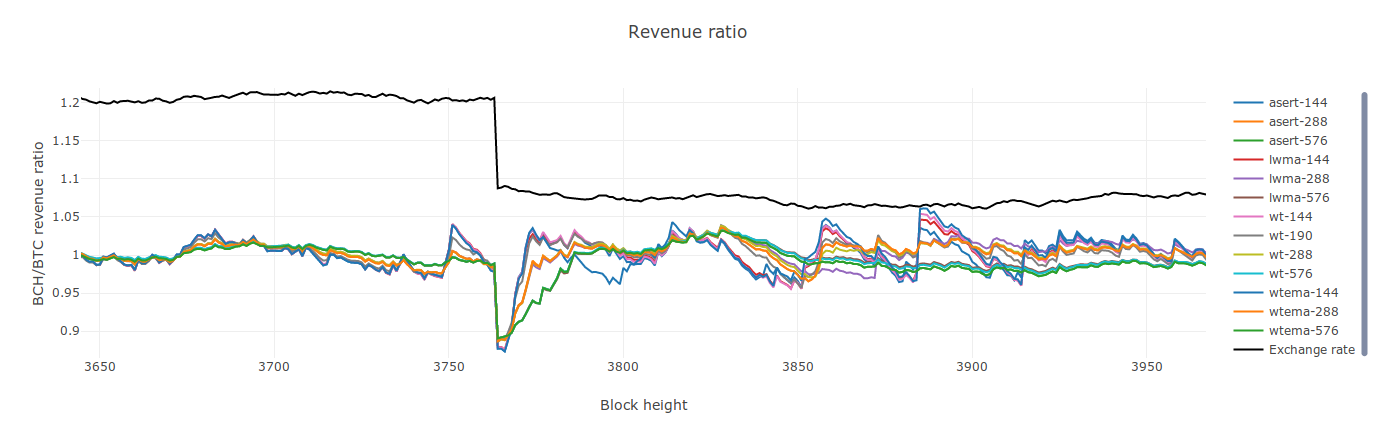
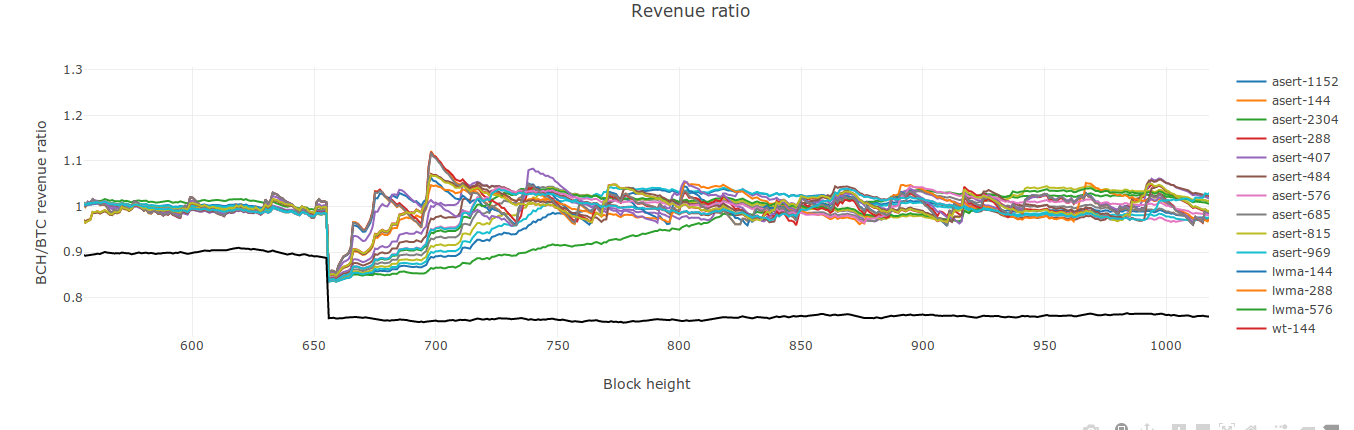




 (from:
(from: 


In a previous issue I discussed this in a different way, received feedback from Mark L, and discussed the possibility of RTT for BCH. This issue discusses everything that came up in a live stream and everything I know of surrounding changing BCH's difficulty algorithm (DA).
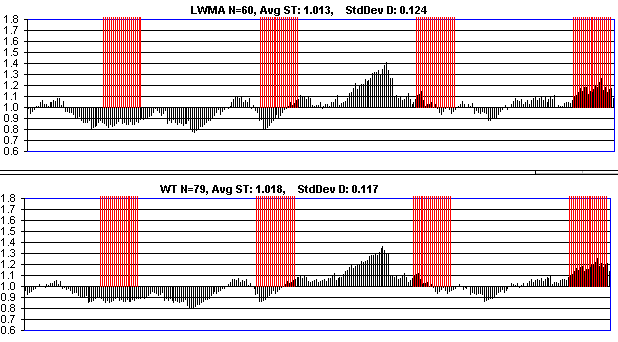
My process to find the "best algo" is this: find a window size parameter "N" for each algo that gives them the same standard deviation for constant HR. This indicates they accidentally attract on-off mining at the same rate. Then simulate on-off mining with step response that turns on and off based on a low and high difficulty value. I have "% delayed" and "% blocks stolen" metrics. Delay: add up a delay qty that is (st - 4xT) for each block over 4xT. Divide that by total blocks to get a % delayed. For "% stolen" I divide time-weighted target that the on-off miner sees by that of dedicated miners. It's how much easier his target was, while he was mining. I just now re-tested 5 DAs. Except for SMA-144, the other 4 below are pretty much the same. WT-190 has slightly lower % stolen but slightly higher delays. (WT-144 is what I kept mistakenly calling wtema in the video). Delays and % stolen are usually a tradeoff. I had been penalizing WT-144 in the past by giving it the same N as LWMA when it needs a larger value.
SMA-144 WT-190 (as opposed to wt-144) LWMA -144 ASERT / EMA - 72 [ update: See my 2nd comment below. In Jonathan's code, this value would be called 72 * ln(2) ]
I'll advocate the following for BCH in order of importance.
There's also sequential timestamps which might be the hardest to do in reality, but important on a theoretical level. It might be possible to enforce sequential timestamps by making MTP=1 instead of 11. Maybe this could prevent bricking of equipment. Sequential stamps (+1 second) must then be able to override local time & FTL. Overriding local time to keep "messages" (blocks) ordered messages is a requirement for all distributed consensus mechanisms. MTP does this indirectly.
Antony Zegers did some EMA code, using bit-shift for division.
EMA is a close enough approximation to ASERT, but here's Mark's tweet on how to do accurate integer-based e^x. https://twitter.com/MarkLundeberg/status/1191831127306031104?s=20
wtema simplifies to:
target = prev_target (1 + st/T/N - 1/N) where N is called the "mean lifetime" in blocks if it were expressed as ASERT, target = prev_target e^(st/T/N - 1/N) The other form of ASERT should give the same results, but the other form of EMA could return a negative difficulty with a large st. [ wtema-144 and asert-144 refer to N = 144 / ln(2) = 208.
If wtema is used: Negative solvetimes (st) are a potential problem for wtema if N is small and delays are long and attacker sends an MTP timestamp. See wt-144 code for how to block them. To be sure to close the exploit, you have to go back 11 blocks. Do not use anything like if (st < 0) { st = 0 } in the DA which allows a small attacker to send difficulty for everyone very low in a few blocks by simply sending timestamps at the MTP.
Std Dev of D per N blocks under constant HR for EMA/ASERT is ~1/SQRT(2*N). This is important for deciding a value for N. If HR increases 10x based on 10% drop in D, you definitely want N > 50 or the DA is motivating on-off mining. On the other hand, being at the edge of motivating on-off mining can reduce the expected variation in D. BTG's Std Dev is about 0.10 when it would have been 0.15 if HR was constant (N=45 LWMA, N=22.5 in ASERT terms). So it's paying a little to on-off miners to keep D more constant. ASERT with N=72 is same as SMA=144 in terms of D variation when HR is constant.
On the other side is wanting a sufficiently fast response to price changes. As a starting point, for ASERT N=100 it takes 6 blocks to rise 5% in response to a 2x increase in HR. This seems sufficiently fast. Std Dev is 1/SQRT(2*100) = 7% per 100 blocks which seems high. 5% accidental changes in D seems to motivate substantial HR changes, so maybe N=200 is better which will have 5% variation per 200 blocks. But this is like LWMA N=400 which would be incredibly smooth and nice if it works but this is 3x larger than my experience. BTG is very happy with LWMA N=45 with Std Dev 10%. Notice that there's bigger bang for the buck with lower N due to the 1/SQRT(N) verses N. You get more speed than you lose stability as you go to lower N. So instead of 200, I would go with 100 or 150.
None of the 60 or so LWMA coins got permanently stuck. About 5% could not get rid of bothersome oscillations. When sending the same random numbers to generate solvetimes, LWMA / EMA / ASERT are almost indistinguishable, so I do not expect them to get stuck either. Most LWMA's are N=60 which has the stability of EMA with N=30. N=100 would have probably been a lot nicer for them, if not N=200 (ASERT N=100). They are mostly T = 120 coins, so they have very fast response, reducing the chances of getting stuck.
Mark was concerned about forwarded timestamps sending difficulty very low which could allow a small attacker to do a spam attack (he would begin with setting a far-forwarded stamp for EMA/ASERT for submission later). To make this a lot harder to so, use st = min(st, 7*600). So long delays will not drop the difficulty as much as "it wants to". Most LWMA's do this as an attempt to reduce oscillations but it may not have helped any.
Combining upper and lower limits on difficulty, timespan, or solvetimes like the 4x and 1/4 in BTC, and the 2 and 1/2 in BCH is what allows unlimited blocks in < 3x the difficulty window. I'm the only one I know of that has described it. A couple of coins following me were the first to see it, losing 5,000 blocks in a couple of hours because I had the hole in LWMA but did not realize it. Some LWMA's had symmetrical limits on st, not just the 7xT upper limit. Removing the 1/2 limit on timespan in BCH will prevent it.
If FTL is dropped, the 70 minute revert from peer to local time rule should be removed (best) or set it to FTL/2 or less. It should be coded as function of FTL. There are a couple of exploits due to Sybil or eclipse attacks on peer time.
A pre-requisite for BFT is that all nodes have a reliable clock that has higher security than the BFT. The clock in POW is each node operator knowing what time it is without needing to consult the network. Any node can unilaterally reject a chain if its time is too far in the future so it's impervious to 99.99999% attacks. (Although current mining on honest chain needs to be > 50% HR of the forwarded cheating chain for the node to continue to reject the cheating chain because time going forward can make the cheating chain become valid.)