Jonas_Santos_170050653
não apagar!
Problema 3: No projeto de uma asa de uma aeronave, deseja-se saber o melhor aerofólio para este perfil. No entanto, deseja-se um valor de coeficiente de sustentação em torno de 0,8 para um ângulo de ataque de 12 graus. Para avaliação do aerofólio, escolheu-se o perfil NACA 0012. O projeto de CFD deve:
- Determinar, com a simulação, um valor de coeficientes de arrasto e sustentação para o aerofólio NACA 0012 para o ângulo de ataque de 12 graus.
- Determinar se está ocorrendo o fenômeno de stall neste ângulo de ataque.
- Usando a simulação apresentada, realizar um estudo paramétrico da modelagem da turbulência para determinar cenários de desempenho aerodinâmico do perfil
não apagar!
Projeto de Dinâmica dos Fluidos Computacional em volta do perfil aerofólio da NACA0012
1. Modelagem
1.1 Objetivo
O objetivo é a análise bidimensional do escoamento ao redor do aerofólio da NACA0012 utilizando como recurso o ANSYS Fluent Software. Utilizando como referência o repositório da Nasa. Tal análise permitirá avaliar parâmetros do escoamento como: de pressão, velocidade e turbulência ao redor das bordas do aerofólio a fim de determinar se estar ocorrendo o fenômeno de stall para o ângulo de ataque de 12 graus.
1.2 Requisitos de Solução
O intuito desse projeto é obter um modelo de cálculo computacional que nos forneça:
-
Valores de arrasto e de sustentação para o ângulo de ataque de 12 graus;
-
Obter informações acerca do stall deste ângulo de ataque.
1.3 Finalidade do Projeto
O projeto possui finalidade acadêmica com o intuito de trabalhar habilidades requeridas para realizar um estudo paramétrico de simulação em Dinâmica dos Fluidos Computacional (CFD). Requerido tanto no meio acadêmico quanto na indústria.
1.4 Hipótese de Simplificações
Com o intuito de simplificar a modelagem do problema, facilitar as definições das condições de contorno, serão adotadas as seguintes hipóteses:
-
Que o escoamento seja 2D;
-
Que o escoamento seja turbulento;
-
Isotérmico.
1.5 Precisão dos Resultados
Como as simulações em CFD é influenciada pela precisão dos resultados. A fim de obter resultados que convergem a uma margem aceitável determina-se um domínio ‘D’ de tal forma que seja 20 vezes o tamanho da corda a partir de um perfil do aerofólio com 200 pontos. Dessa forma estabelece como precisão mínima de 5%.
1.6 Geometria do Problema

Figura 1: Domínio D
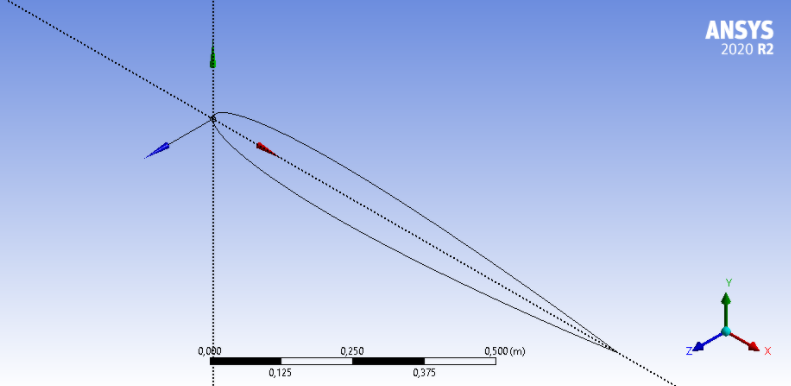
Figura 2: Perfil do aerofólio com 200 ponto
### 1.7 Metodologia
A melhor metodologia a ser aplicada nesse caso é o estudo CFD pois tem como principal vantagem a facilidade da simulação visto que para realizar o mesmo estudo, como por exemplo, em túnel de vento normalmente envolvem a forte interação entre a estrutura do modelo e o escoamento. O que significa que não apenas a estrutura deve ser corretamente modelada, mas também o escoamento além de suas características especificas de acordo com o ambiente no qual será utilizada. Uma modelagem correta em túnel de vento resulta que os parâmetros adimensionais de semelhança sejam exatamente os mesmos na estrutura real e no modelo. Entretanto a duplicação completa desses parâmetros é impraticável ou na maioria das vezes impossível.
### 1.8 Prazo de Entrega
O projeto é dividido em três etapas, sendo elas: Modelagem; Pré-Processamento e Processamento. O prazo de entrega para este trabalho será para o dia 04 de dezembro de 2020.Dessa forma a segmentação das principais partes sendo:
|Etapa do Projeto |Período |
|--------------------------------------------|----------|
|1ª Etapa: Modelagem |10 dias |
|2ª Etapa: Pré-Processamento |20 dias |
|3ª Etapa: Processamento e Pós-Processamento |45 dias |
|4ª Etapa: revisão |05 dias |
## 2. Pré-Processamento
### 2.1 Domínio e Geometria
O domínio, nesse projeto, é uma região na qual será realizado os cálculos numéricos essa região contínua é discretizada por uma malha que representa pequenos volumes de controle.A geração de malha é um processo de transformação de um domínio contínuo para um domínio discreto.O domínio ao redor do aerofólio é de 20 vezes o tamanho da corda na vertical e 10 na horizontal. O perfil é traçado a partir de 200 pontos de modo a satisfazer a precisão requerida.
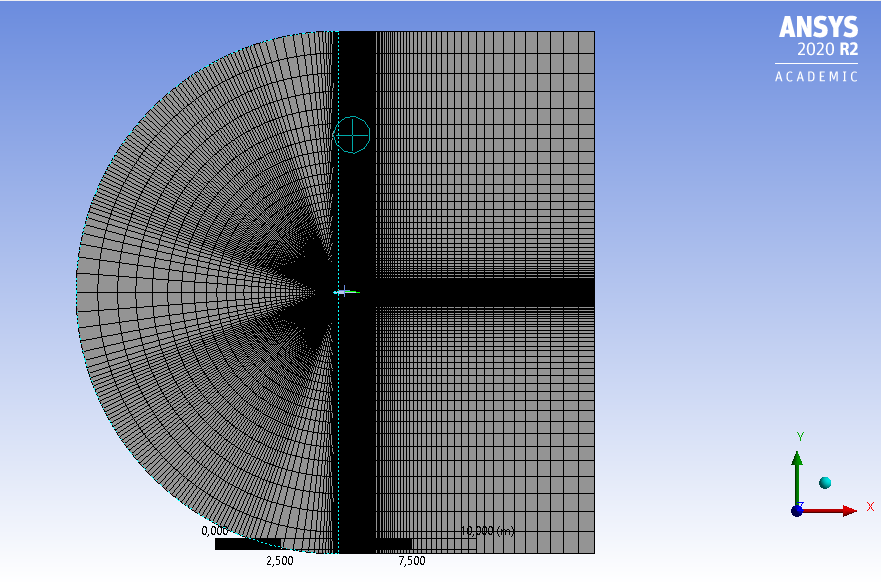
### 2.2 Malha
A malha foi obtida a partir da segmentação do domínio em 6 partes gerando uma malha hexaédrica a partir do modelo SpalartAllmaras, ao redor do perfil (y+ menor do que 5). Sendo essa uma malha não estruturada composta de elementos quadriláteros com volumes finitos. Na condição da malha está adequada utilizam um software de calculadora online para o Y+.
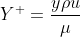
Analisando a malha mais de perto para verificar se obedece a condição estipulada para Y+.
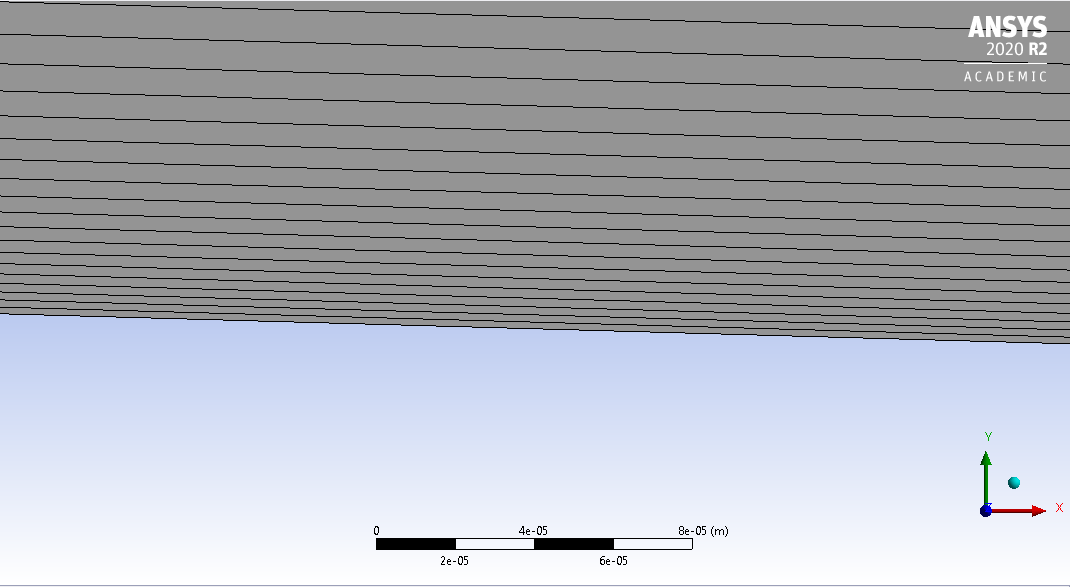
Visto que para o número de Reynolds estabelecido nesse projeto estabeleceram o valor de Y plus < 1. O Y+ fornece uma distância entre a superfície do aerofólio até a parede menor ou igual a 4.5e-6. Ele é necessário para essa simulação para avaliação da malha estabelecida. Dessa forma como o Y+ foi satisfeito a malha gerada é de alta qualidade.
### 2.3 Inputs
* Re = 6000000;
* Massa específica do ar de 1,2754 kg/m3;
* Escoamento incompreensível (Ma<0.3);
* u=88.65m/s;
* Ma = 0.258.
### 2.4 Escolhas do pré-processamento no Fluent
A partir do repositório da Nasa, utilizado na validação de resultados e comprovação dos métodos utilizados nessa simulação, tem-se a velocidade e ângulo de ataque da entrada de fluido. Estes valores são de 88,65m/s e 0ºgraus.Entretanto o objetivo desse projeto é obter os coeficientes de sustentação e arrasto para o ângulo de 12ºgraus além de obter Informações acerca do stall deste ângulo de ataque. O software é inicializado de forma hibrida e a simulação é realizada com 5000 iterações.
A seguir os principais valores de entrada:
| Número de Reynolds |6000000 |
|-----------------------------------|--------------|
| Massa específica do ar |1,2754 kg/m3 |
|Velocidade |u=88.65m/s |
|Escoamento incompressível (Ma<0.3) |Ma = 0.258 |
|Viscosidade |1.81E-5 Km /ms|
|Para traçar o domínio| |
|-----------------------------------|--------------|
|H |H1=10m|
|V |V1=20m|
|Solver| |
|-----------------------------------|--------------|
|Pressure-Based |Velocity formulation:Absolute|
|Time : steady |2D Space planer|
|Viscosus Model| |
|-----------------------------------|--------------|
| |Scarlat-Allaras ( 1 eqn) |
|Scarlat-Allaras | Straing velocity based |
|Options |Curvature correction |
| Inlet| |
|-----------------------------------|--------------|
|Velocity Specification Method |Magnitude and direction|
|Velocity magnitude |88.65 m/s |
|Turbulence | |
|-----------------------------------|--------------|
|Specfication method |Turbulance Viscosity radio|
|Turbulence viscosity ratio |1 |
|Outlet||
|-----------------------------------|--------------|
|Specfication method| Turbulance Viscosity radio|
|Turbulence viscosity ratio| 1|
|Wall| |
|-----------------------------------|--------------|
|Wall motion |Stationary wall|
|Shear condition |no slip|
|Wall roughness| |
|-----------------------------------|--------------|
|Roughness models | standard|
|Roughness height(m) |0|
|Roughness constant |0.5|
|Reference Values| |
|-----------------------------------|--------------|
|Area(m2) | 1 |
|Density(kg/m3) |1.225 |
|Depth(m) | 1|
|Enthalp(j/kg) |0 |
|Lenght(m) |1 |
|Pressure(pa) |0 |
|Temperature(K) |288.16 |
|Velocity(m/s) |1 |
|Viscosity(kg/m-s) |1,79E-01|
|Ratio of specific heats |1.4 |
|Yplus for heat tran.coef |300 |
O modelo para escoamento SpalartAllmaras utiliza apenas 1 equação para descrever o problema ele é baseado em deformação e vorticidade. O escoamento estabelecido como 2D, em regime permanente, sendo incompreensível (Ma<0.3)e isotérmico. Os parâmetros de entrada utilizam o método magnitude and Direction que será utilizado para mudar o ângulo de ataque de 0º para 12º graus.
### 2.5 Recursos Computacionais
## 3. Processamento e Pós-Processamento:
### 3.1 Histórico de convergência
Emprega-se um teste para o ângulo de ataque de 0° graus a fim de comparar os valores obtidos com o repositório da NASA, seguindo os critérios de precisão estabelecidos nesse projeto. As figuras abaixo mostram o valor dos coeficientes ao longo das iterações.
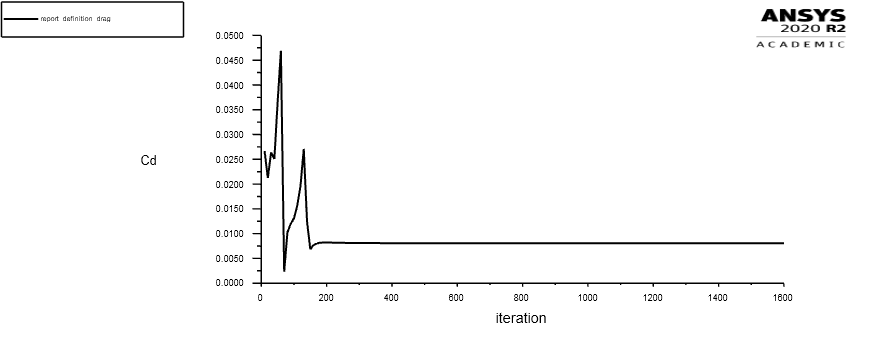
Figura 5: cd para o ângulo de ataque de 0°graus
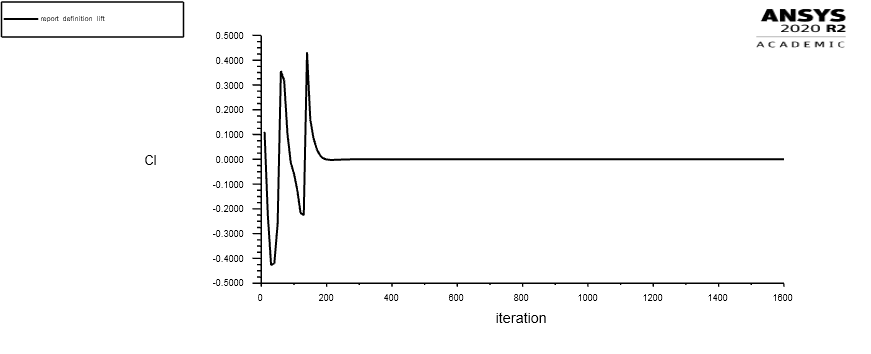
Figura 6: cl para o ângulo de ataque de 0°graus
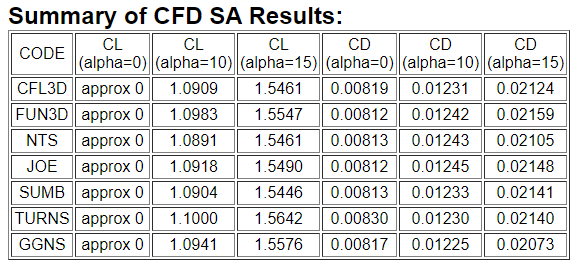
No início do projeto foi estipulado um erro aceitável de até 5% para isso compara-se os valores obtidos de cl e cd para o esse ângulo de ataque com o repositório de referência.

Sendo a fórmula do erro:
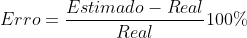
Substituindo os valores:
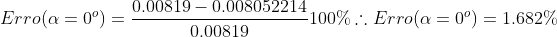
Para o cl de cordo com o repositório da NASA possui valor aproximadamente zero. Nesse projeto obtém-se o valor cl = 1.470869e-06, muito próximo do que foi requerido. Como o erro foi menor que o estipulado para esse projeto o histórico de convergência do cálculo está adequado.
### 3.2 Residuais
Os residuais precisam diminuir para 1e-3. Então, isso significa que não importa de onde o residual começa, ele deve finalmente diminuir para 1e-3. Como nessa simulação os resíduos se encontram em valores próximos a 1e-05, significando que o resultado convergiu bem.
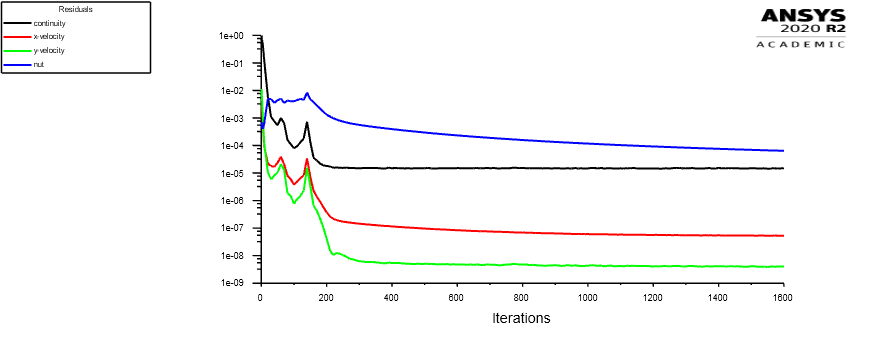
Figura 7: residuais para o ângulo de ataque de 0°graus
### 3.4 Tempo de Processamento
A inicialização ocorreu de forma hibrida com 5000 interações. Cada interação varia em 1e-4. Cada interação ocorreu média de 0,600s. Dessa forma o processo de simulação geral teve aproximadamente 3000s .
### 3.5 Análise da física do escoamento
Observa-se que não ocorre variações bruscas de pressão e velocidade para o ângulo de ataque de 0° graus. O que descreve a natureza fisica do experimento um vez que o perfil do aerofólio é simétrico e não produz sustentação a 0º que pode ser observado a partir dos valores dos coeficientes de arrasto e sustentação.
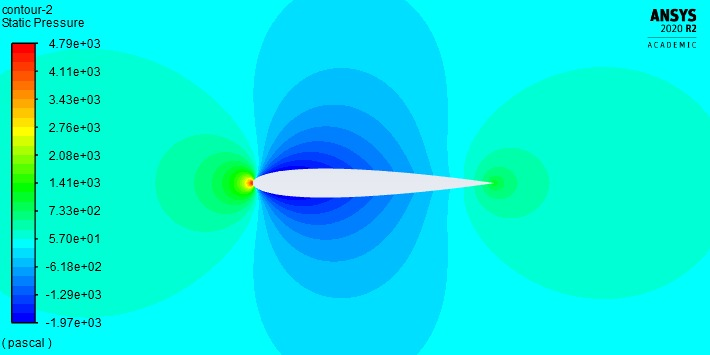
Figura 8: Pressão para o ângulo de ataque de 0°graus

Figura 9: velocidade para o ângulo de ataque de 0°graus
## 4. Análise para o ângulo de ataque de 12 graus
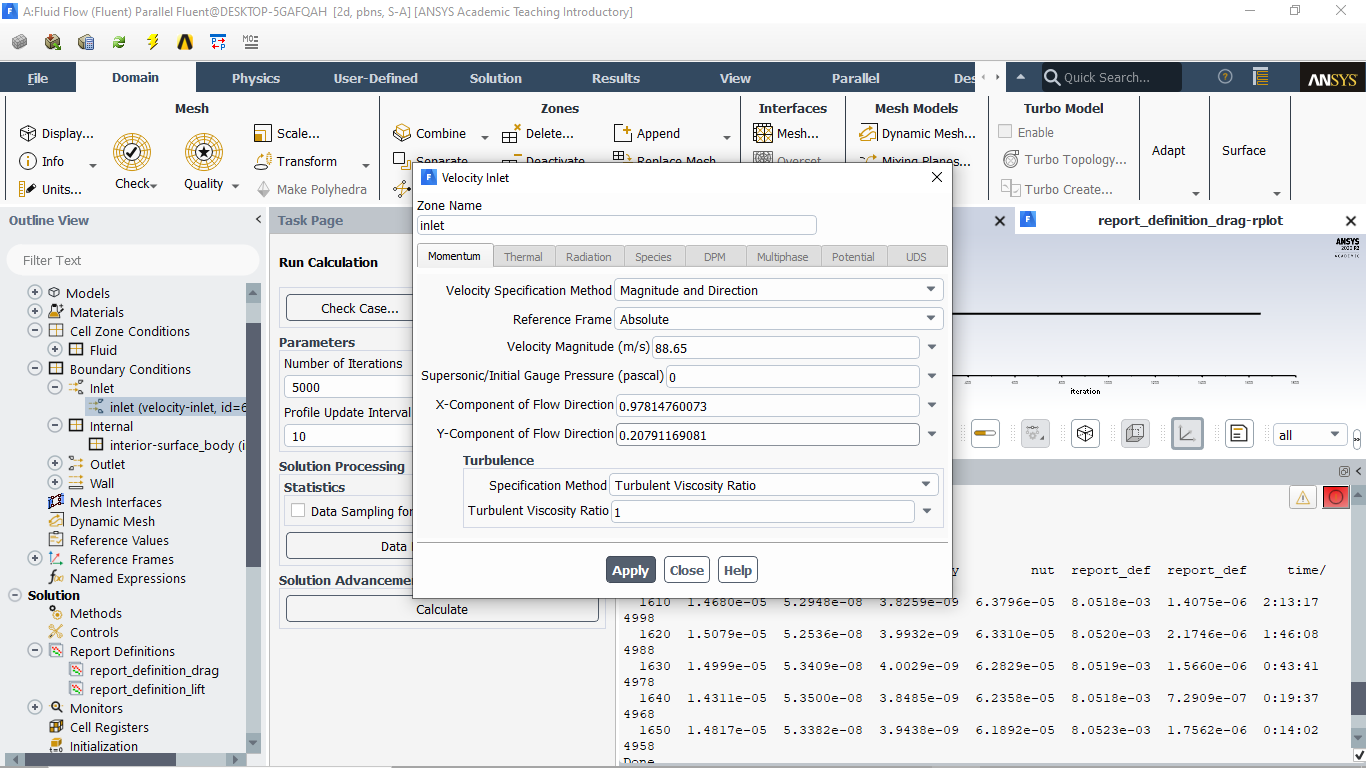
O motivo de reiniciar a simulação para o ângulo de ataque de 12° tem como finalidade satisfazer o objetivo do projeto, que por sua vez, é realizar uma análise que permitirá avaliar parâmetros do escoamento como: de pressão, velocidade e turbulência ao redor das bordas do aerofólio a fim observar a ocorrência ou não do fenômeno de stall para esse o ângulo de ataque. Assim deverão substituir os valores de setup em relação ao ângulo de ataque assim utilizarão os valores de seno e cosseno para o ataque de 12 graus.
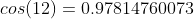
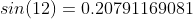
Substitui-se os parâmetros de entrada nas condições de borda.
O repositório de definições tanto do Drag quanto do lift ficam:
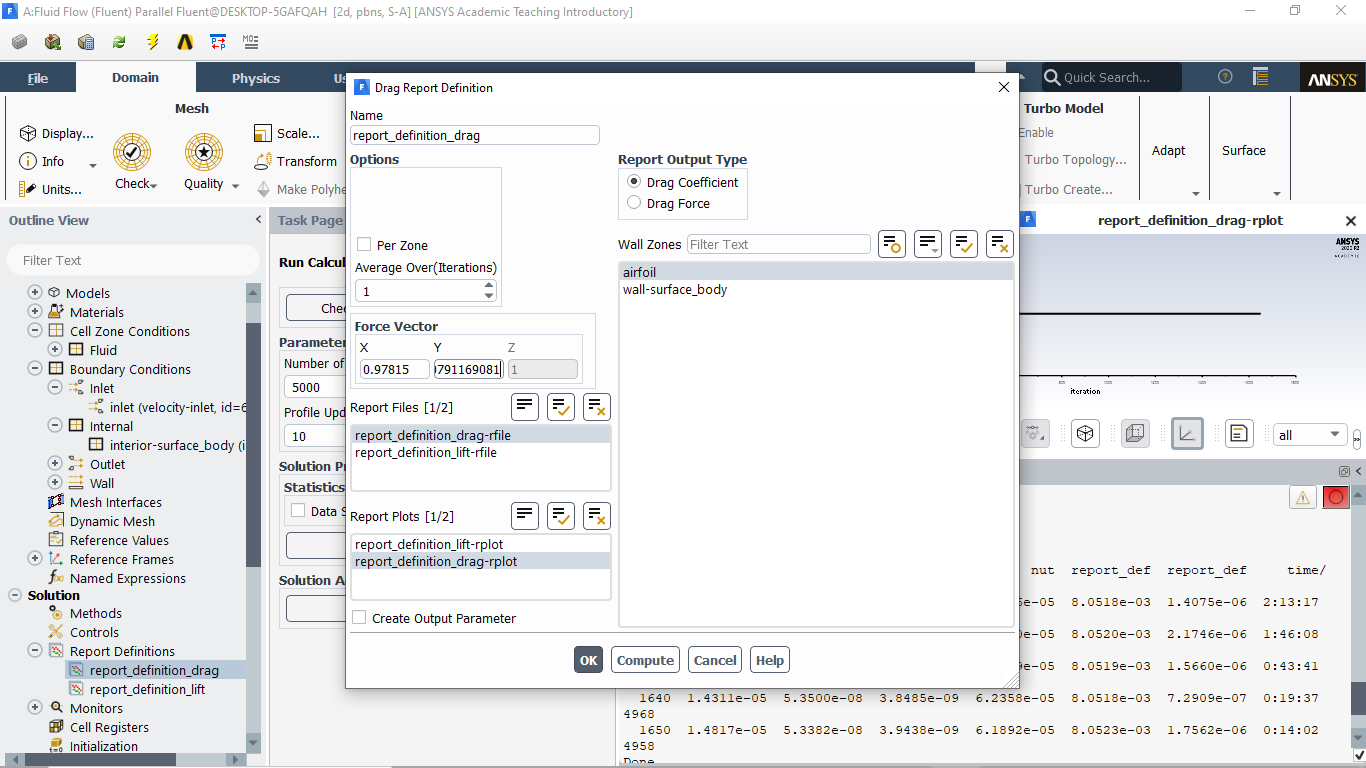
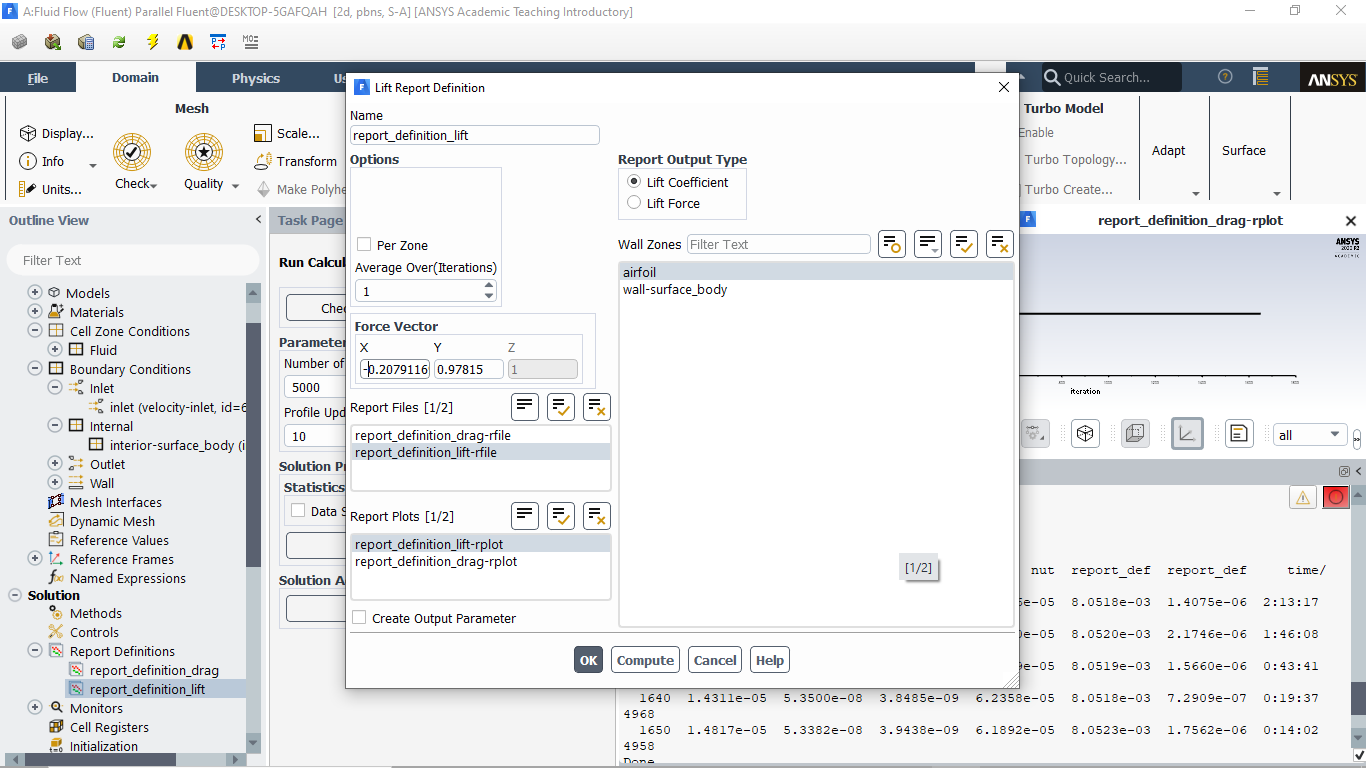
É importante salientar que em relação ao valor de X do lift colocarão - sin(12), pois lift e drag são sempre relativos a movimentação do fluido. Sendo lift perpendicular ao drag enquanto o drag está na direção do movimento do fluido.
### 4.1 Análise da física do escoamento
Segundo os gráficos das condições de contorno para o ângulo de ataque de 12° observam que aparecerá uma força de sustentação, uma vez que na parte inferior do aerofólio, a pressão é maior e a velocidade é menor que na parte superior. Pode ser demonstrado pela lei de Bernoulli que em pontos específicos do aerofólio onde tem um acréscimo nos gradientes de pressão e descrêssemos nos gradientes de velocidade.
A força de sustentação é a componente da resultante aerodinâmica perpendicular à direção do vento relativo, sendo uma força útil ao aerofólio. A força de arrasto é a componente da resultante aerodinâmica paralela à direção do vento relativo, sendo nociva e deve ser reduzida ao mínimo possível.
Percebe-se que com o aumento do ângulo de ataque houve, como esperado, uma mudança significativa entre as diferenças de pressão no intradorso quanto no extradorso. Observa-se que a pressão na parte inferior do perfil é maior que na parte superior. Nota-se com o aumento do ângulo de ataque as velocidades ao logo do perfil não estão mais constantes quanto guando estava posicionada em 0 graus.
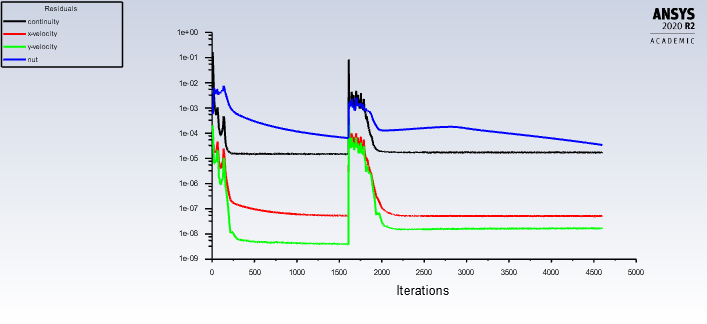
Figura 11: valores residuais para o ângulo de ataque de 12°graus
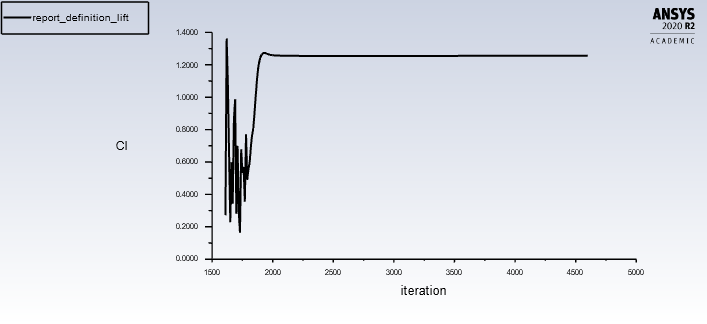
Figura 12: valores de cl para o ângulo de ataque de 12°graus
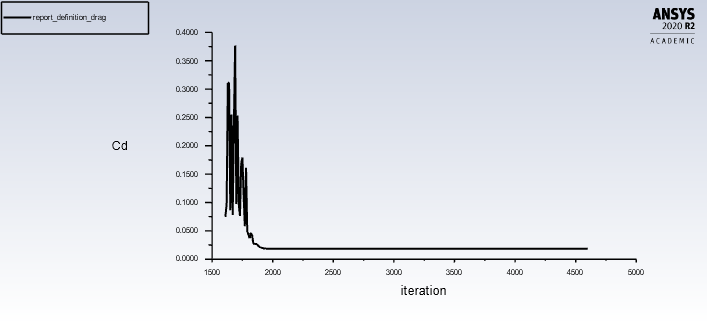
Figura 13: valores de cd para o ângulo de ataque de 12°graus
Comparando os valores e calculando o erro:
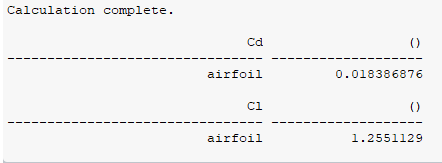
Utiliza como referência os valores tabelados no repositório da NASA. Obtém-se:
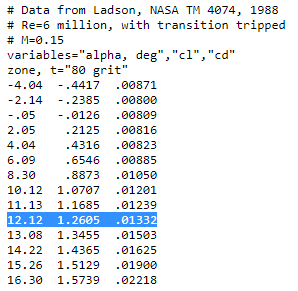
Dessa maneira o erro do cl será de:
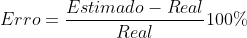
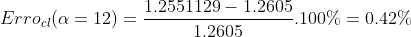
enquanto o do cd:
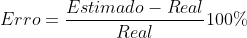
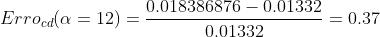

Figura 14: Pressão para o ângulo de ataque de 12°graus

Figura 15: Velocidade para o ângulo de ataque de 12°graus

Figura 16:Turbulence viscosity ratio para o ângulo de ataque de 12°graus
# Conclusão
Portanto, de maneira geral, segundo os gráficos acima não está ocorrendo o fenômeno de *stall* para o ângulo de ataque de 12 graus. Mostra que a ferramenta CFD é bastante poderosa para resolver diversos problemas da indústria em geral e de pesquisa, pois é fiel em seus resultados e condizente com a física em geral.
# Referências
Fox, R.W., McDonald, A.T. and Pritchard, P.J.; “ Introdução à Mecânica dos Fluidos”, LTC, 6a ed. (2004)
Anderson Jr., John D., Mateus, Fundamentos de Engenharia Aeronáutica: Introdução ao Voo 6aed.