证书

想象日常访问网站的场景，用户在使用浏览器客户端（Google、Safari等）访问Gmail的网站，输入www.mail.google.com的域名，客户端会先访问DNS服务器，获取该域名对应的IP地址，然后根据该IP地址链接Gmail的服务器

但存在被攻击的情况

比如：黑客截获访问DNS的请求，然后发送一个不正确的IP地址给用户，该假的IP地址，可能会提供一个Web网站，获取不知情用户下提交的账户和密码，甚至最终给你跳转到正确的Gmail网站上，在不知情的情况下被人获取了密码

在90年代中期，人们想出了证书的使用：SSL、TLS、HTTPS

同样适用gmail的场景，gmail存放自身网址所对应的私钥，人们访问gmail时，会通过私钥验证是否真正是gmail，而私钥是通过gmail网址向CA（==证书授权部门==）申请授权颁发的

当用户访问数据时

访问gmail.com，同时提供一个随机数
gmail.com返回给用户证书，以及上述随机数通过私钥的签名
用户根据该签名，可以在CA中通过CA保存的public key（公钥）来进行验证

想象下在这种情况下攻击访问过程的例子，设置一个流氓服务器，截获了用户的DNS请求，此时流氓服务器不能给用户提供gmail的私钥！也就不能给用户提供可以在CA中验证的签名

CA 监管不当引起的新需求

由于证书颁发机构的兴起，出现了数百个CA，此时引起了多起证书颁发机构事件制造假证书的案例

==解决该问题的可能性是拥有一个包含所有有效证书的单一在线数据库==

问题在于：

不知道如何区分正确颁发的有效证书和伪造证书，因为通常情况下，不知道DNS名称的真正所有者是谁
此外，还需要允许证书所有者更改证书颁发机构或续订他们的证书，或者他们可能丢失了私钥、需要一个新的证书了来更换他们的旧证书
即使技术上有可能区分正确的证书和伪造的证书，没有所有人都信任的实体来做这件事

此时，CT应运而生。CT（Certifcate Transparency）是一个所有人都可以验证的提供证书的方式

Certificate Transparency（CT）

CT 启动类似于审计的功能，CT是一个是所有信息公开的系统

他甚至允许假证书的颁发，但是该系统能确保这些证书是公开的，人们能看到该证书，包括拥有这个证书的所有人名称

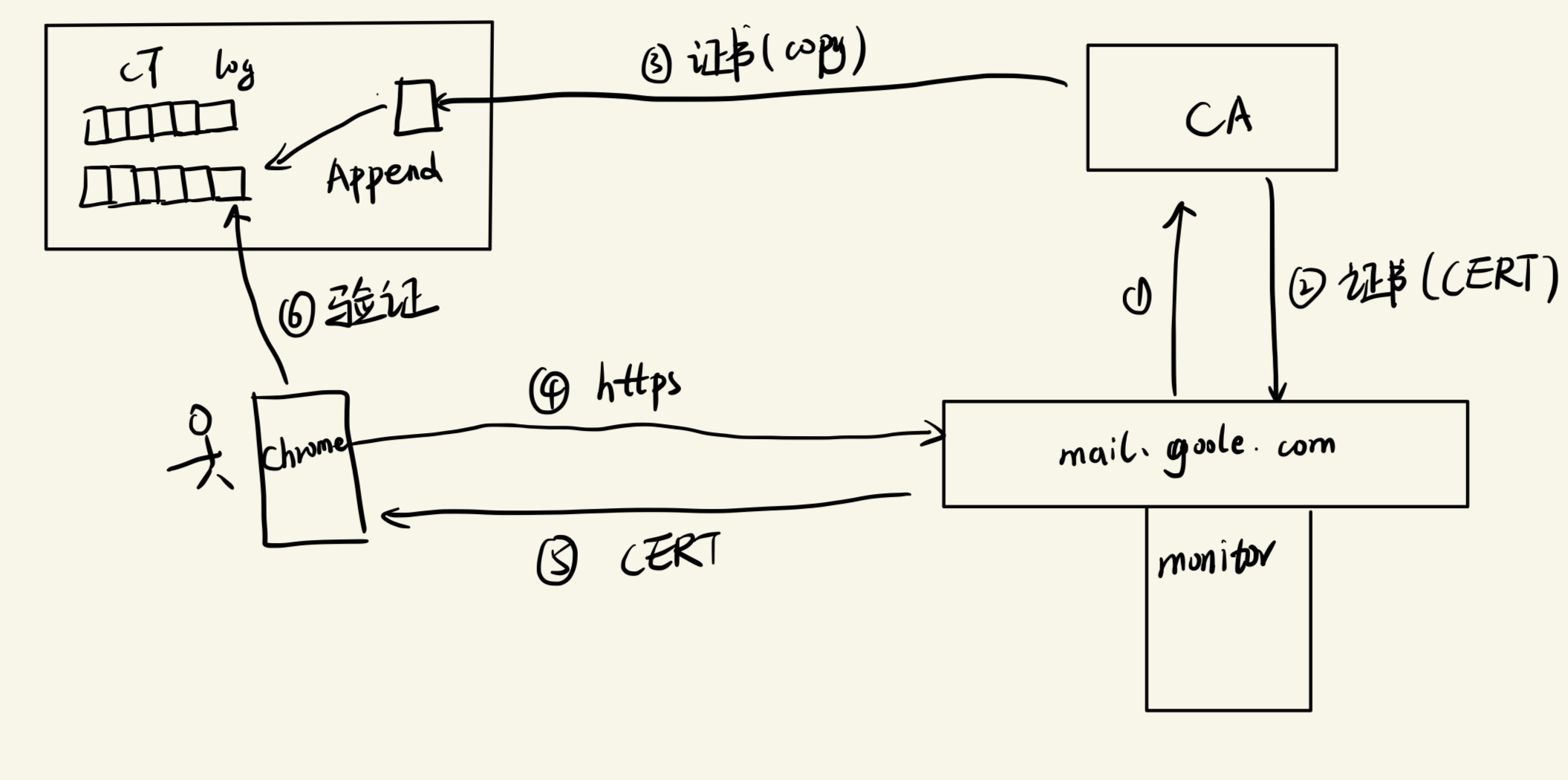
流程

gmail向CA 申请证书
CA 向 gmail返回该域名对应的证书
CA 向 CT 中写入该证书
用户通过Chrome 浏览器访问gmail网站
gmail 返回给用户该证书
用户此时可以拿着这个返还的证书向CT中校验，看是否是真实无误的证书

Gmail.com 还维护一个监视器，定期与证书日志服务器对话，他将知道有哪些日志在日志服务器里

如果某个流氓CA给gmail.com 颁发不正确的证书（该证书会被写入到日志服务器中），MONITOR可以在日志服务器中偶然发现它

CT 的特点

独立、可靠的日志

CT 依赖于独立、可靠的日志，因为它是一个分布式生态系统。日志使用 Merkle 树构建，可公开验证、仅附加且防篡改
日志可公开获取并受到监控

感谢 CT，域名所有者、浏览器、学者和其他感兴趣的人可以分析和监控日志。他们能够查看哪些 CA 在何时以及为哪些域颁发了哪些证书。
通过运行 CT 日志来保护网络

为了帮助确保网络安全，CT 需要由不同组织、不同司法管辖区运行的大量可靠日志。

CT 可能是由 Google 的工程师发起的，但它之所以有效，是因为独立组织设置并运行监视器和日志。为了互联网，也为了互联网

CT的完整使用流程

网站所有者向证书颁发机构 (CA) 请求证书

证书将域和公钥联系在一起。证书透明度与 Web PKI/SSL 证书系统配合使用，提供透明度和验证。仅附加日志是防篡改的，用户代理检查日志在加密上是否一致，并且证书颁发机构的监视器将检查可疑日志。
CA颁发预证书

CA 收到域所有者的证书请求。它检查域所有者是否有权请求证书，并创建一个预证书，将域与公钥联系起来。 预证书包含证书的所有信息。它还具有有毒扩展（poison extension），因此用户代理不会接受它。 预证书有助于打破 CT 领域的僵局。在 CA 记录证书之前，证书需要 SCT（签名证书时间戳）。但要使证书获得 SCT，需要将其提交到日志。
CA 将预证书发送到日志

任何人都可以向日志提交证书，但大多数是由 CA 提交的。当 CA 将其中一项提交到日志时，日志会使用签名证书时间戳 (SCT) 进行响应。这是在称为最大合并延迟 (MMD) 的时间段内将证书添加到日志的承诺。
预证书已添加到日志中
日志维护证书的记录。他们使用一种特殊的加密机制，即默克尔树，来允许公共审计。日志是：
- 仅追加。证书只能添加到日志中，不能删除、修改或追溯插入。
- 加密保证。 他们使用 Merkle 树来防止篡改和不当行为。
- 可公开审核。任何人都可以查询日志并验证其行为是否良好，或者验证 SSL 证书或预证书是否已合法附加到日志中。
Merkle 树是简单的二叉树，由叶子和节点组成。在 CT 中，叶子是已附加到日志中的各个证书的哈希值。 节点是成对子叶或成对子节点的哈希值。所有节点和叶子都源于根哈希，它也是一棵 Merkle 树。当日志服务器对根 Merkle 树进行签名时，它会创建一个签名树头 (STH)。 日志会定期将所有新证书附加到日志中。 它使用新证书创建一个单独的 Merkle 树哈希。 然后，它将这棵 Merkle 树与旧的 Merkle 树结合起来，形成一棵新的 Merkle 树。 然后对新的 Merkle 树哈希进行签名以创建新的签名树头。
日志将 SCT 返回给 CA

每个日志都会立即向 CA 返回一个 SCT，并承诺在最大合并延迟(MMD)内包含该证书。 MMD 通常为 24 小时：此时间跨度旨在让日志操作员有时间修复出现的任何问题，然后再将其从批准的日志列表中排除。 MMD 还有助于确保日志不会阻止证书的颁发或使用。

CA 使用 X.509v3 扩展将 SCT 附加到证书。他们签署证书并将证书交付给服务器操作员。（还有另外两种不太常见的方法可以实现此目的：OCSP 装订和 TLS 扩展。）CT 不需要服务器修改，因此服务器运营商可以按照他们一贯的方式管理 SSL 证书。
CA 将证书发送给域所有者

SCT 伴随证书的整个生命周期。服务器必须在 TLS 握手期间传递带有证书的 SCT。（TLS 握手是指加密通信的双方相互验证并同意使用哪些加密算法和密钥。在这里，当用户访问 HTTPS 网站并且 Web 服务器响应 HTTPS 请求时，该过程就开始了。）
浏览器和用户代理有助于确保网络安全

某些浏览器（例如 Chrome 和 Safari）有助于实施 CT。

日志数量以及 CA 选择记录的日志选择均由用户代理策略决定。 Safari 和 Chrome 用户代理都需要至少 2 个 SCT，具体取决于证书的生命周期。
日志受到加密监控

监视器是公共运行的服务器。他们定期联系所有日志服务器并监视可疑证书。监控人员与网站运营商合作，帮助他们了解是否为某个域颁发了未经授权的证书。他们可以监视具有异常扩展或权限的证书，例如具有 CA 功能的证书。监控器可以高效、快速地证明所有证书都已一致地附加到日志中。

他们还可以证明特定证书已附加到日志中。对于检查特定日志的一致性的监视器，它本身计算一致性证明，然后使用它来验证日志的一致性。 一致的更高版本包含早期版本中的所有内容，并遵循旧版本中的条目。

如果监视器需要验证日志中是否存在特定证书，它可以自行计算审核证明并使用它来验证该证书是否存在。

一些监控器由公司和组织运行。其他服务将作为域名所有者和证书颁发机构的订阅服务运行。个人也可以运行自己的监视器

CT 所需要满足的日志属性

需要：

对于长度为 N 的日志中的任何特定记录 R，我们可以构造一个长度为 O(lg N) 的证明，允许客户端验证 R 是否在日志中。
对于客户端观察到并记住的任何较早的日志，我们可以构造一个长度为 O(lg N) 的证明，允许客户端验证较早的日志是当前日志的前缀。
审核员可以有效地迭代日志中的记录。

CT在此类日志中发布TLS证书，谷歌浏览器使用这些属性，

使用属性(1) 来验证增强验证证书是否已记录在已知日志中。
使用属性 (2) 确保接受的证书以后不会在未被检测到的情况下从日志中消失。
使用属性 (3) 允许审核员在以后随时扫描整个证书日志，以检测错误颁发或被盗的证书。

所有这一切都是在不盲目相信日志本身运行正常的情况下发生的。相反，日志的客户端（Chrome 和任何审核员）会在访问日志时验证日志的正确操作。（所有人对日志的正确性持怀疑态度，都可以进行验证）

这篇文章解释了这种可验证的防篡改日志（也称为透明日志Transparency Log）的设计和实现。首先，我们需要一些加密构建块。

此时Merkle Tree 完美的契合了所需要的日志属性

Merkle Tree

加密Hash、身份验证、承诺

在介绍Merkle Tree之前，先简单介绍一下加密的一些内容

Hash 函数：可以将任意大小的消息M 映射为一个固定大小的输出 H(M)

利用该性质，在实践中产生任何一对具有相同哈希值 H(M1) = H(M2) 的不同消息 M1 ≠ M2 是不可行的。

传统加密算法SHA-1在95年提出，在17年破解，现在使用的加密算法为SHA-256，但未来依然会被破解

（未损坏的）加密哈希函数提供了一种将少量可信数据引导为大量数据的方法。

加密过程

两个人同时拥有文件的SHA-256哈希值（只有两个人有），发送文件后，接收方可以使用该hash值对文件的进行检查。

SHA-256 哈希可以验证文件的真实性，它只有 256 位。

单个哈希可以是任意大量数据的认证或承诺，但验证则需要对整个数据集进行哈希处理。为了允许对数据子集进行选择性验证，我们不仅可以使用单个哈希，还可以使用哈希的平衡二叉树，称为 Merkle 树。

Merkle Tree 概念

Merkle Tree 由N个节点构成，其中N是2的幂
每条记录都被独立的计算Hash，产生N个Hash值
然后各自根据各自的hash值，两两合并，构建新的上一级Hash，逐层往上构建

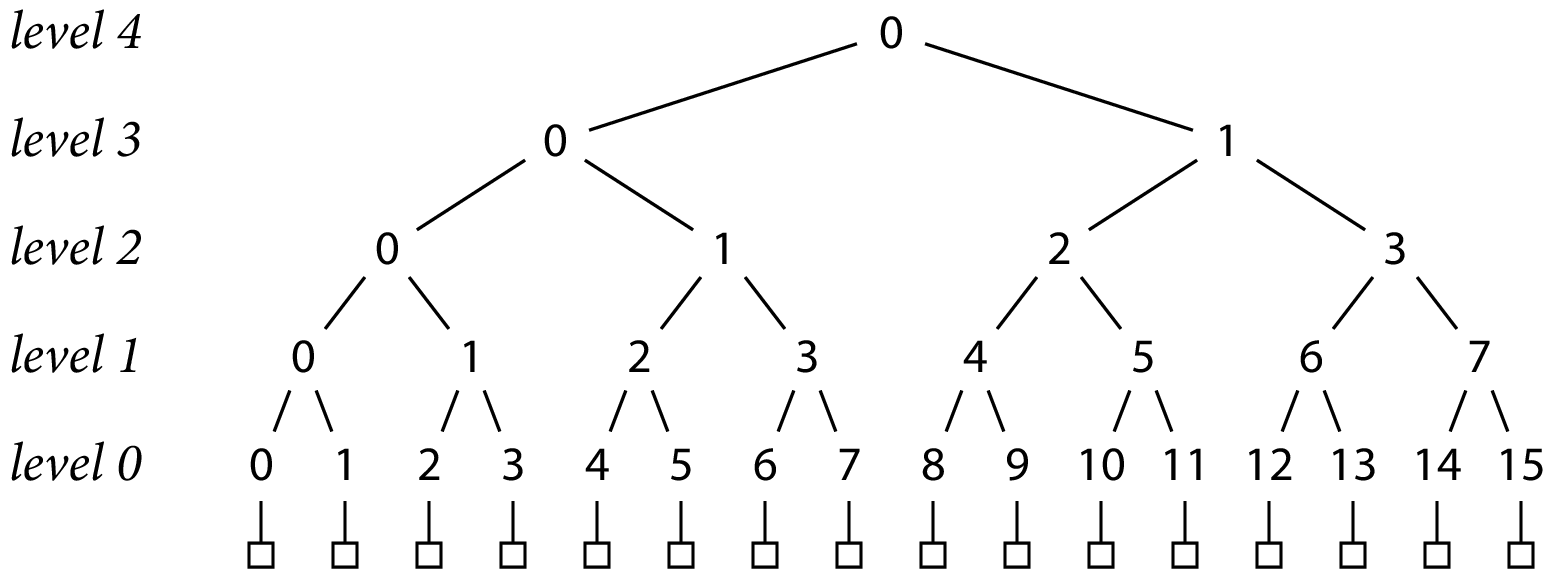
样例

底部的方框代表 16 条记录。树中的每个数字表示一个散列，输入通过向下的线连接。我们可以通过坐标来引用任何哈希：L 级哈希数 K，我们将其缩写为 h(L, K)。在级别 0，每个哈希的输入是单个记录；在较高级别，每个哈希的输入是来自较低级别的一对哈希

$$h(0,K)=H(record K) \h(L+1,K) = H(h(L,2K),h(L,2K+1))$$

为了证明特定记录包含在由给定top-level 散列表示的树中（即，允许客户端验证记录，或验证先前的承诺(commitment)，或两者兼而有之），==只需提供所需的散列即可根据记录的哈希值重新计算总体顶级哈希值。==

例如，假设我们想要证明某个位串 B 实际上是具有top-level 哈希树T（总共有16条记录）上的第9条记录。我们可以提供这些位以及重建整个树哈希所需的其他哈希输入使用这些位。具体来说，客户可以像我们一样得出：

T = h(4, 0) = H(h(3, 0), h(3, 1)) = H(h(3, 0), H(h(2, 2), h(2, 3))) = H(h(3, 0), H(H(h(1, 4), h(1, 5)), h(2, 3))) = H(h(3, 0), H(H(H(h(0, 8), h(0, 9)), h(1, 5)), h(2, 3))) = H(h(3, 0), H(H(H(h(0, 8), H(record 9)), h(1, 5)), h(2, 3))) = H(h(3, 0), H(H(H(h(0, 8), H(B)), h(1, 5)), h(2, 3)))

h(L,K): h: L层的第K个hash数值的缩写

由该公式可知，验证Level 0的第9条数据，只需要第3层第0条Hash 值（h(3.0)）和第0层的第8条Hash值(h(0,8))，第一层的第5条数据(h(1,5))，第二层的第三条数据(h(2,3))，以及所需要验证数据的原始文件记录(H(B))

[h(3.0),h(0,8),h(1,5),h(2,3),H(B)]

此时我们可以验证文件内容B，来自于T这个Merkle 树上

实际上，证明 B 是带有哈希 T 的 Merkle 树中的记录是通过以 H(B) 作为输入给出 T 的可验证计算来完成的。

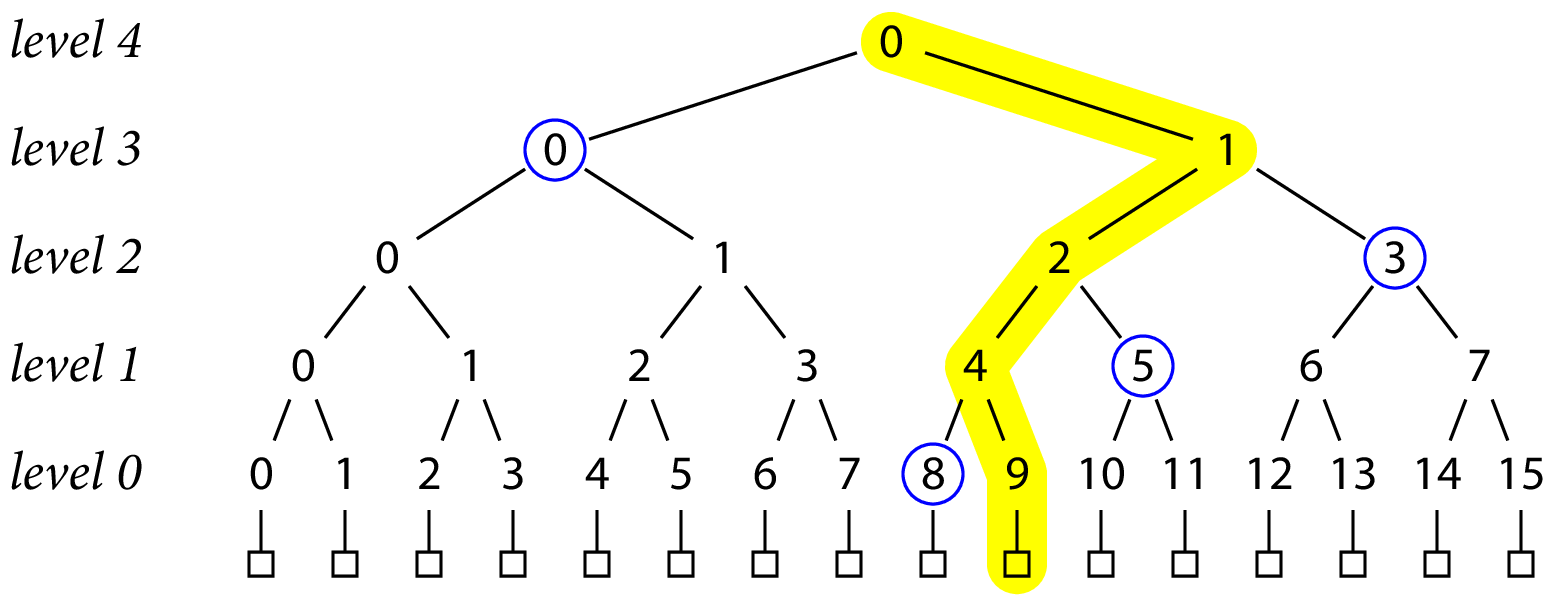
从图形上看，证明由从被证明的记录到树根的沿路径（以黄色突出显示）的节点的兄弟散列（以蓝色圈出）组成。

一般来说，证明给定记录包含在树中需要 lg N（本例中是$log_216 = 4$, 分别对应图中的蓝色圆圈节点）个哈希值，==根以下的每一层都有一个哈希值。==

将我们的日志构建为在 Merkle 树中散列的记录序列将为我们提供一种编写有效（lg N 长度）证明特定记录在日志中的方法。

但是有两个相关的问题需要解决：

我们的日志需要定义为任意长度 N，而不仅仅是 2 的幂，
我们需要能够编写一个有效的证明，证明一个日志是另一个日志的前缀

Merkle 树状结构日志

为了将 Merkle 树推广到非 2 的幂大小（任意数字，不是1、2、4、8、16这类二进制的幂次结果），==我们可以将 N 写为 2 的递减幂之和==，然后为输入的连续部分构建这些大小的完整 Merkle 树，最后对at-most-lg N(位于当前二进制幂次结果数量级的最大值) 个完整的树一起生成单个顶级哈希。例如，13 = 8 + 4 + 1；

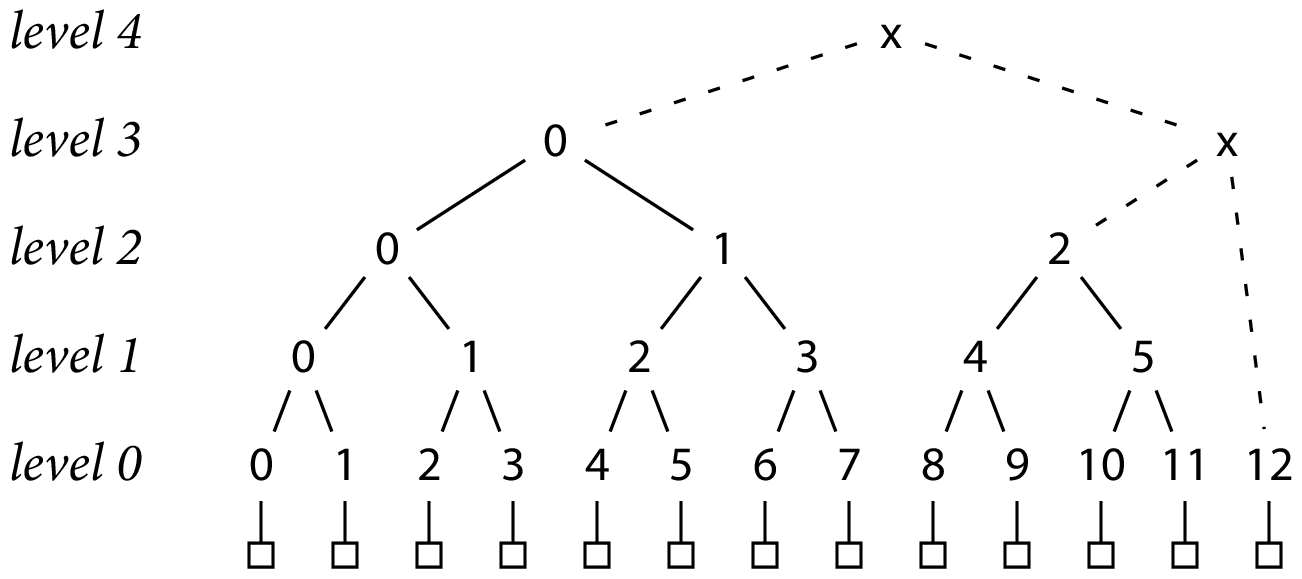
==标记为“x”的新哈希组合了完整的树，从右到左构建，以生成整体树哈希==。请注意，这些散列必然结合不同大小的树，因此来自不同级别的散列；例如，h(3,x) = H(h(2,2), h(0,12))

==完整 Merkle 树的证明策略同样适用于这些不完整的树==。例如，记录 9 在大小为 13 的树中的证明是 [h(3, 0), h(0, 8), h(1, 5), h(0, 12)]：

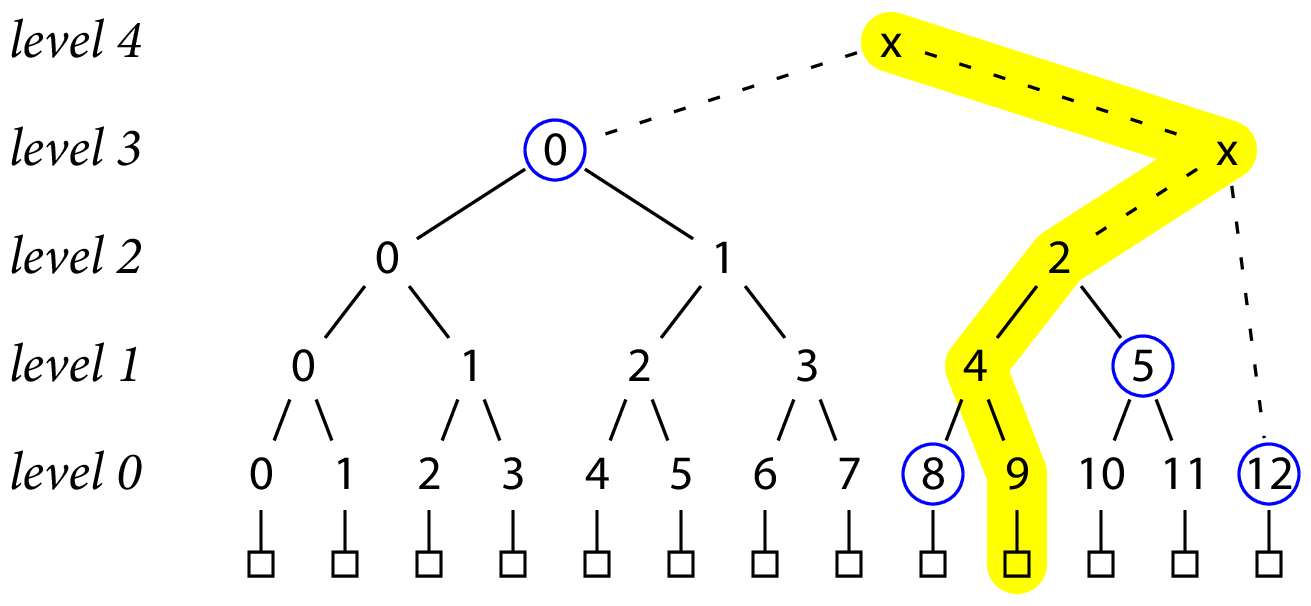
==请注意，h(0, 12) 包含在证明中，因为在 h(3, x) 的计算中它是 h(2, 2) 的同级。==

证明完整 Merkle 树的证明策略同样适用于这些不完整的树

需要证明：具有树哈希 T 的大小为 N 的日志是具有树哈希 $T^{'}$的大小 $N^{'}( > N)$的日志的前缀。

为了证明树哈希T的日志包含在树哈希$T^{'}$的日志中，我们可以遵循相同的思路：给出T和$T^{'}$的可验证计算，其中T计算的所有输入也是计算的输入德克萨斯州。例如，考虑大小为 7 和 13 的树：

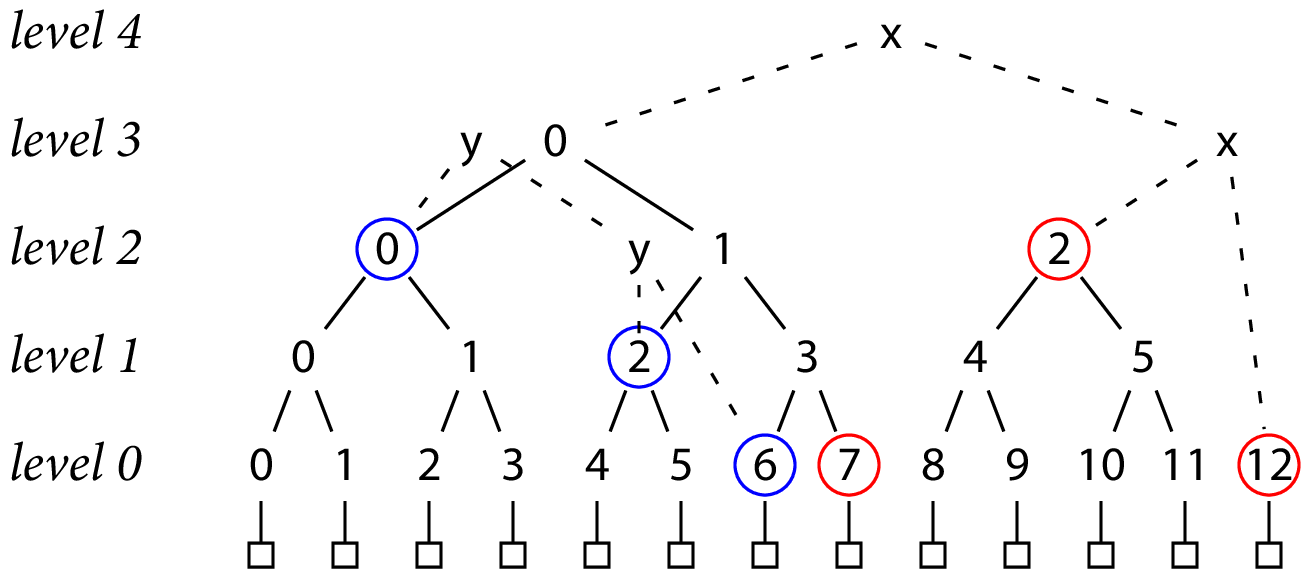
在图中，“x”节点使用哈希 T₁₃ 完成大小为 13 的树，而“y”节点使用哈希 T₇ 完成大小为 7 的树。

为了证明T₇的叶子包含在T₁₃中，我们首先以完整子树的形式给出T₇的计算（蓝色圆圈），（没有考虑右侧不完整子树）：

$T₇ = H(h(2, 0), H(h(1, 2), h(0, 6)))$

然后我们给出 T₁₃ 的计算，根据需要扩展哈希以暴露相同的子树。这样做会暴露同级子树（用红色圈出）：

T₁₃ = H(h(3, 0), H(h(2, 2), h(0, 12)))

= H(H(h(2, 0), h(2, 1)), H(h(2, 2), h(0, 12)))

= H(H(h(2, 0), H(h(1, 2), h(1, 3))), H(h(2, 2), h(0, 12)))

= H(H(h(2, 0), H(h(1, 2), H(h(0, 6), h(0, 7)))), H(h(2, 2), h(0, 12)))

假设客户端知道树的大小为 7 和 13，它可以自行导出所需的分解。我们只需要提供哈希值 [h(2, 0), h(1, 2), h(0, 6), h(0, 7), h(2, 2), h(0, 12)]。 客户端重新计算哈希值隐含的 T₇ 和 T₁₃，并检查它们是否与原始值匹配。

请注意，这些证明仅使用完整子树的哈希值，即编号哈希值，而不是组合不同大小子树的“x”或“y”哈希值。

编号的哈希值是永久性的，从某种意义上说，一旦这样的哈希值出现在给定大小的树中，相同的哈希值将出现在所有更大大小的树中。相比之下，“x”和“y”哈希值是针对单个树计算的，并且不会再次出现。

因此，两个不同大小的树的分解所共有的散列必须始终是永久散列。 较大树的分解可以利用暴露的同级树的临时哈希值，但我们可以轻松地仅使用永久哈希值。在上面的示例中，从 T₇ 的部分重建 T₁₃ 使用 h(2, 2) 和 h(0, 12)，而不是假设访问 T₁₃ 的 h(3, x)。避免临时哈希将最大记录证明大小从 lg N 哈希扩展为 2 lg N 哈希，并将最大树证明大小从 2 lg N 哈希扩展为 3 lg N 哈希。请注意，大多数顶级哈希（包括 T₇ 和 T₁₃）本身就是临时哈希，需要最多 lg N 个永久哈希来计算。例外情况是两倍大小的树 T₁、T2、T₄、T₈ 等。（结合完整树图看）

Merkle Tree 应用： Storing a Log

对每个文件单独哈希，然后生成一个256位长的hash码

这种情况下,只有这些日志记录的这个序列才能产生那个hash值，找不到其他的替代来生成与此日志项序列相同的最终树哈希

最顶层的哈希值称之为签名树头（STH，Signature Tree Head），日志服务器把这个缓存放在树的顶部，用他们的私钥签名，然后把它交给客户、浏览器和监视器。此结果已经产生，就不能否认该签名由该日志的所有人产生，方便捕获流氓CA

一旦日志服务器表现了一个特定的STH给浏览器和监视器，该STH会被提交到一些特定的日志内容中，因为他将无法产生不同的日志内容来生成相同的hash，所以本质上来说，这个hash值应该是一种承诺

Storing a Log

存储日志只需要一些仅附加文件

CA发送新证书添加到日志中：会添加一个新的树头(此时讲解的是按照2的倍数数量添加到日志系统上)，随着CA的不断添加，日志也不会不断增长，会产生一系列越来越高的树头

第一个文件保存连接的日志记录数据。第二个文件是第一个文件的索引，包含一系列 int64 值，给出第一个文件中每个记录的起始偏移量。该索引允许通过记录号有效地随机访问任何记录。

日志还会存放某些文件中每个记录的"起始偏移量"

“Efficient generation of proofs”（有效生成证明）类似于某个文件的偏移量

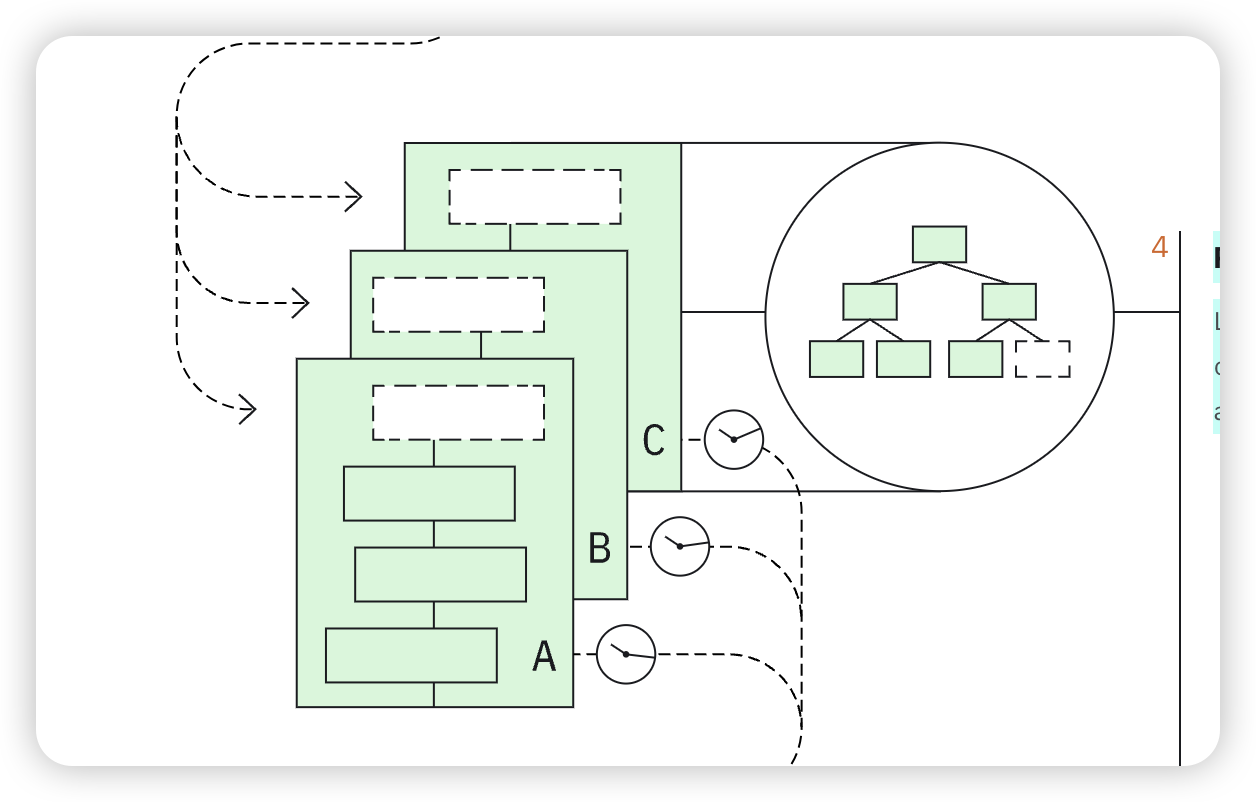
正如我们在上一节中指出的，树之间存在显着的共性。 特别是，最新的哈希树包括所有早期哈希树的所有永久哈希，因此“仅”存储最新的哈希树就足够了。

一种简单的方法是维护 lg N 个仅附加文件，每个文件在树的一层保存哈希序列。由于哈希值是固定大小的，因此可以通过从文件中适当的偏移量读取来有效地读取任何特定的哈希值

写入新的日志记录的步骤：

将记录数据追加到数据文件中
将数据的偏移量追加到索引文件中
将数据的哈希值追加到0级哈希文件中。
如果在 0 级哈希文件中完成了一对哈希，则将该对的哈希追加到 1 级哈希文件中；如果完成了一级哈希文件中的一对哈希，我们将该对的哈希附加到二级哈希文件中；依此类推。每个日志记录写入都会将一个散列附加到至少一个、最多 lg N 个散列文件，每次写入平均略低于两个新散列。（具有 N 个叶子的二叉树有 N–1 个内部节点。）

除了上述写入新的日志记录的方法外，还可以

将lgN 个仅追加哈希文件交错为单个近追加文件
1. 目的：让日志仅存储在Record data、Record index、和Hashes中
将日志文件存储在一对数据库表中，一个用于记录数据，一个用于散列（数据库本身可以提供记录索引

==无论是在文件中还是数据库表中，日志的存储形式都是追加的==，因此缓存的数据永远不会过时，从而使得拥有日志的并行只读副本变得微不足道

相反，写入日志本质上是集中式的，需要对所有记录进行密集的序列编号（并且在许多情况下还需要抑制重复）。

使用双表数据库表示的实现可以将写入的复制和协调委托给底层数据库，特别是如果底层数据库是全局复制且一致的，例如 Google Cloud Spanner 或 CockroachDB。（有点儿贴合CA的原理）

Serving a log（提供日志服务）

仅仅存储日志当然是不够的，我们还必须将其提供给客户

请记住，每个使用日志的客户端都对日志的正确操作持怀疑态度。日志服务器必须使客户端能够轻松验证两件事：

任何特定记录都在日志中
当前日志是先前观察到的较早日志的仅附加扩展。（比如记录事务，当前完成的最新事务，是在之前所有事务执行的结果之上完成的）

为了发挥作用，日志服务器还必须能够在给定某种查找键的情况下轻松查找记录（使用偏移量等，或者直接使用数据存储），并且它必须允许审核员迭代整个日志以查找不属于的条目。

为了完成这两个任务，日志服务器必须回答五个查询

Lastest():返回当前日志大小和顶级哈希值，由服务器进行加密签名以确保不可否认性。
RecordProof(R,N):返回记录 R 包含在大小为 N 的树中的证明。
TreeProof(N,N'):返回大小为 N 的树是大小为 NX 的树的前缀的证明。
Lookup(K):返回与查找键 K 匹配的记录索引 R（如果有）。
Data(R):返回与记录 R 关联的数据

Verifying a log

客户端使用前三个查询来维护其观察到的最新日志的缓存副本，并确保服务器永远不会从观察到的日志中删除任何内容。

当想知道Web服务器刚刚给出的证书是否在日志系统中，他会拿着该证书询问日志系统，该日志服务器将返回该证明、证书在日志上的位置，以及一些其他内容，由客户本地自己来判断该证书是否合法（因为日志服务器有可能作假）

用户浏览器也会保存一部分日志服务器的index（保存日志偏移量的内容）

当用户访问时，通过浏览器保存的STH（只保存了STH的信息）的信息，访问STH上保存的hash值

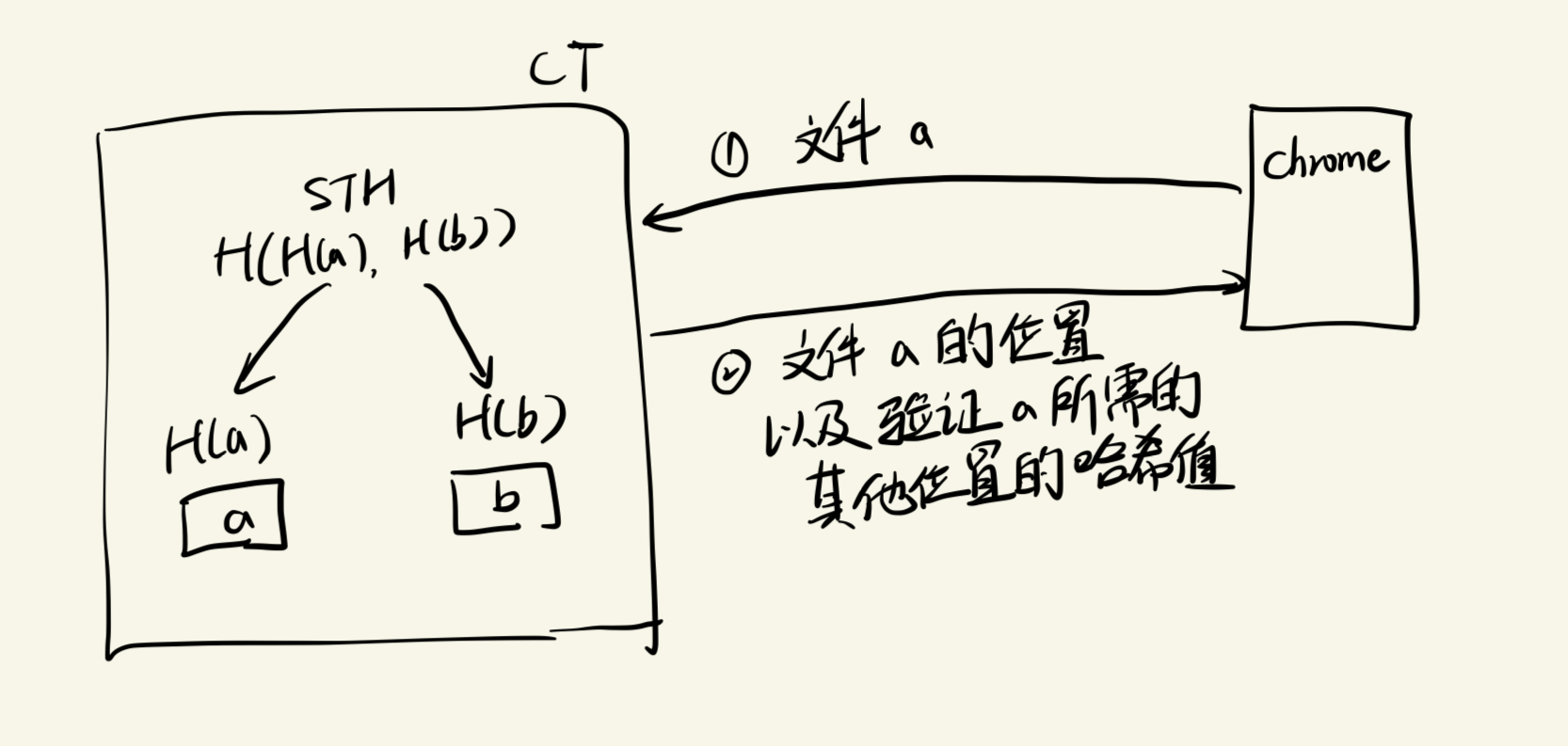
为此，客户端缓存最近观察到的日志大小 N 和顶级哈希 T。

然后，在接受数据位 B 作为记录号 R 之前，

客户端验证 R 是否包含在该日志中。如果有必要（即，如果 R ≥ 其缓存的 N）

客户端会将其缓存的 N、T 更新为最新日志的内容，但前提是验证最新日志包含当前缓存日志中的所有内容。在伪代码中：

validate(bits B as record R):
if R >= cached.N // R不在缓存的日志中
    N,T = server.Latest()  // 获取新的日志大小和顶级哈希T
    if server.TreeProof(cached.N,N) cannot be verified: // 如果前缀证明没有成功，则报错
        fail loudly
    cached.N cached.T = N, T //保存新的N和T
if server.RecordProof(R,cached.N) cannot be verified using B: // 验证R包含在大小为N的树上的证明
    fail loudly
accept B as record R

客户端的证明验证确保日志服务器行为正确，至少从客户端的观察来看是这样。

Summary

综上所述，我们已经了解了如何发布具有以下属性的透明（防篡改、不可变、仅附加）日志：

客户端可以使用 O(lg N) 下载字节来验证任何特定记录。
客户端可以使用 O(lg N) 下载字节来验证任何新日志是否包含旧日志。
即使对于很大的日志，这些验证也可以在 3 个 RPC（每个约 8 kB）中完成。
用于验证的 RPC 可以很好地代理和缓存，无论是为了网络效率还是可能为了隐私。
审核员可以遍历整个日志以查找错误条目。
写入N条记录定义了N个哈希树的序列，其中第n棵树包含2 n – 1个哈希值，总共N2个哈希值。但不需要存储 N2个哈希值，而是可以将整个序列压缩为最多 2N 个哈希值，从特定树重建特定哈希值最多需要 lg N 次读取。
这些 2N 哈希值本身可以压缩为 1.06N 哈希值，代价是可能读取 8 个相邻哈希值以从 2N 中重建任何一个哈希值。（文章中的Tiles 过程带来的效果）

总体而言，这种结构使得日志服务器本身本质上是不可信的。它无法在不被发现的情况下删除观察到的记录。 它无法对一个客户撒谎，除非该客户永远处于另一条时间线上，从而通过与另一客户进行比较来轻松检测。日志本身也很容易被代理和缓存，因此即使主服务器消失，副本也可以继续为缓存的日志提供服务。最后，审计员可以检查日志中是否存在不应该存在的条目，以便可以从日志的使用中异步验证日志的实际内容。

Fork Consistency

在上一节验证的过程中时

假设日志服务器说慌，但此时它已经暴露了自己的STH，包含A、B日志，日志服务器想诱骗客户端进入虚假的浏览器

此时假设日志服务器中并没有该证书，但是它假装他在，它就需要给你提供证明，此时除了要提供x的位置外，还需要另一个同一层次的hash值 y,使得

$H(H(x),H(y)) = STH = H(H(a),H(b))$

这只是有两个日志的情况，如果是多级N个节点的Merkle Tree，则需要大概$log_2 N-1$个这样的数据

如果狡猾的服务器可以区分各个客户端，它仍然可以向不同的客户端提供不同的日志，以便受害客户端看到从未暴露给其他客户端或审核员的无效条目。

但是，如果服务器确实对受害者撒谎，那么受害者要求任何以后的日志都包含它之前看到的内容，这一事实意味着服务器必须保持谎言，永远提供包含谎言的备用日志。这使得最终检测到的可能性更大。

例如，如果受害者通过代理到达或将其缓存的日志与另一个客户端进行比较，或者如果服务器在向哪些客户端撒谎方面犯了错误，则不一致很容易暴露。要求服务器签署最新（）响应使得服务器不可能否认不一致，除非声称已完全受到损害。

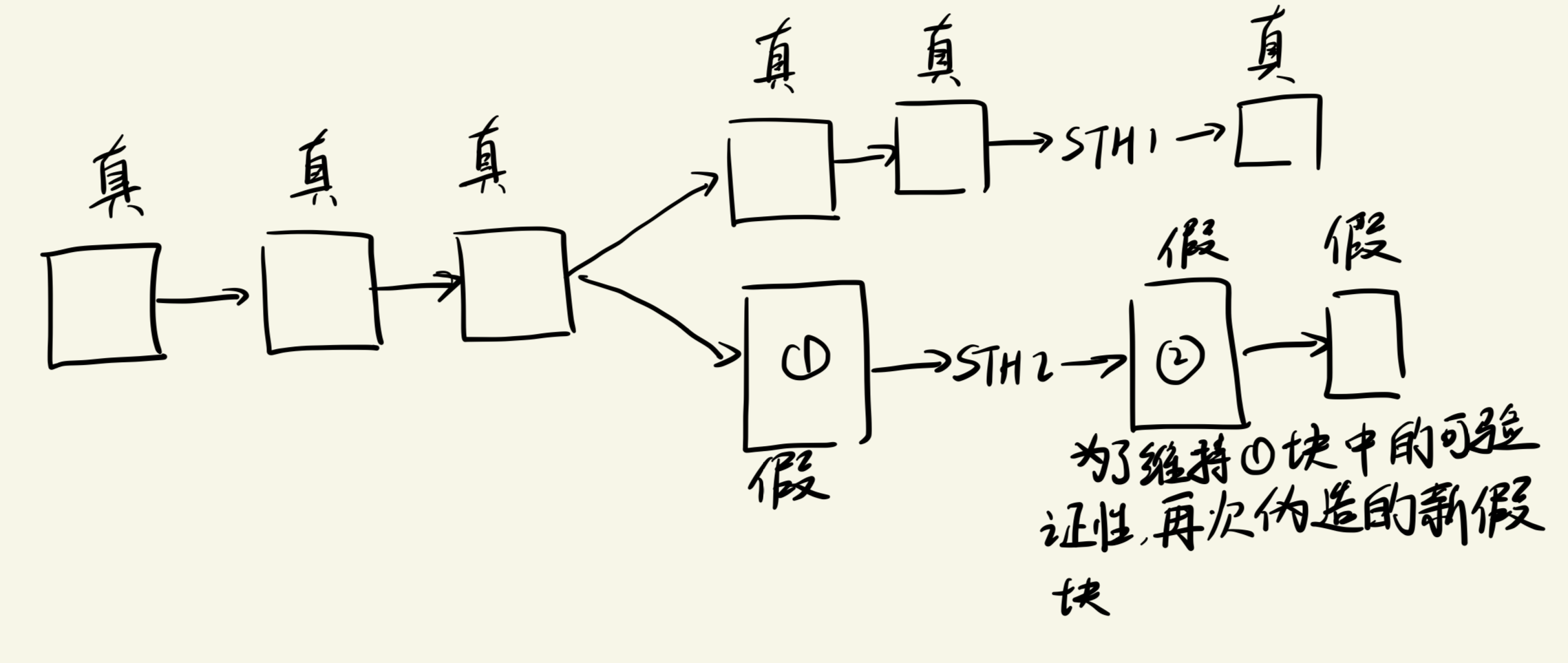
客户端检查有点像 Git 客户端如何维护自己的远程存储库的缓存副本，然后在 git pull 期间接受更新之前，验证远程存储库是否包含所有本地提交。

区别：但透明日志客户端只需要下载 lg N 哈希值来进行验证，而 Git 会下载所有缓存的 N – N 个新数据记录，更一般地，透明日志客户端可以有选择地读取和验证日志中的各个条目，而无需需要下载并存储整个日志的完整副本（不需要比较完整的日志数据）。

意味着日志服务器需要找到两个不同的输入，并且产生相同输出的哈希函数，这对于哈希密码来说是不可能的

总结：此时，即出现了分叉的情况，只不过在Merkle Tree的帮助下，即使有人伪造了某个证书，并且能通过Hash本次的Hash验证，但随着其他证书的加入，为了能一直伪造证书的合法性，需要不断伪造新的hash值来满足Hash验证，这在理论上来说是不可能实现的，因此Merkle Tree 实现的日志系统能保证一条完全合法的证书日志，以此实现了Fork consistency。

实际场景

在本处讲的像是单一服务器提供CA验证，但实际上由多个服务器组成，当Chrome 实际上需要证书和证书颁发机构的时候，Chrome 提交他们所有的证书到多个日志服务器上，==不同的日志服务器实际上并不保存相同的日志==，约定是证书颁发机构将提交一个新的证书来说明。

比如有五个不同的日志服务器，实际上在网站告诉浏览器的证书信息中，它包括证书的日志服务器的标识，日志服务器的日志中有证书，因此你的浏览器知道要与哪些日志服务器对话

为什么要有多个：

当发生损害
当被证明是恶意的时候，

他们不比完全相同，只要有一个日志中保存了证书即可

良好的日志服务器应该有不分岔的日志，通过监视器和浏览器

只要出现可以日志，监视器最终一定会注意到

通常情况下，CT的日志服务器分散在各地，而浏览器供应商只有少数几个

思考

有时候如果想不出防止不良行为的方法，也许你可以建造一些至少可用的东西，比如此处使用的审计，而不是通过阻止，这往往比防止坏事容易得多

Merkle Tree 的一些替代

Merkle Tree的一些缺点：

Merkle Tree 更适合对Array数组求Hash，人们提出了一些其他方式来针对其他数据类型

Merkle Patricia Tree

也叫Radix Tree，和Trie

用于针对Map构建merkle 树

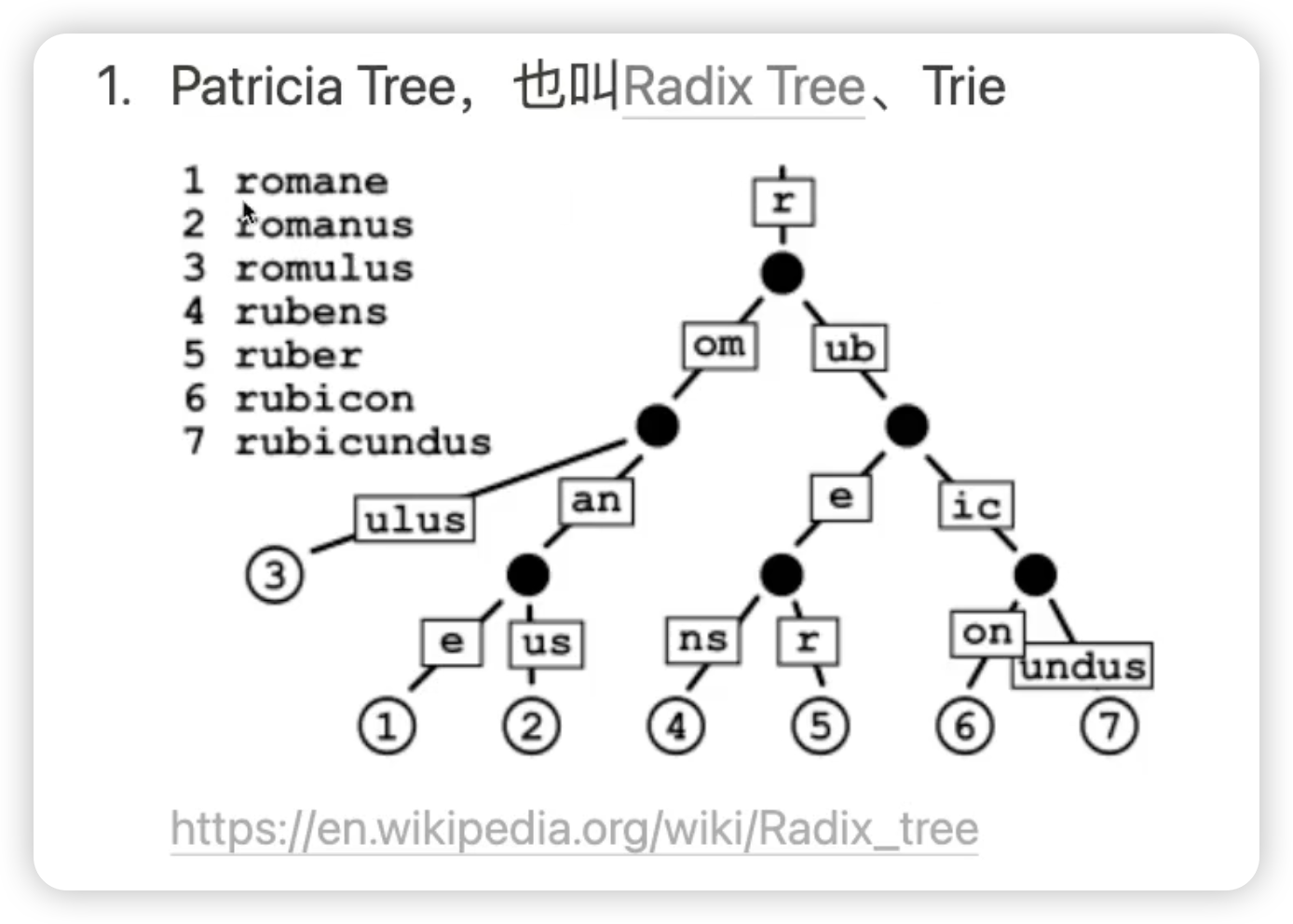
左上角为Map中的数据，key在右边，Value在左边

Trie 是Map的一种数据结构，根据key的前缀进行索引
1. 类比Hash Map（hash+bucket），Binary search Tree：比较key的大小
Patricia Tree 理解为Trie的一种优化实现，对相同路径的node进行了聚合
Patricia Tree 的特点在于
1. 高效支持按key前缀的范围查找
2. 🌲结构的确定性，和插入顺序无关
3. 增删查的时间复杂度是O（k），k是key的长度
4. 理解和实现起来简单

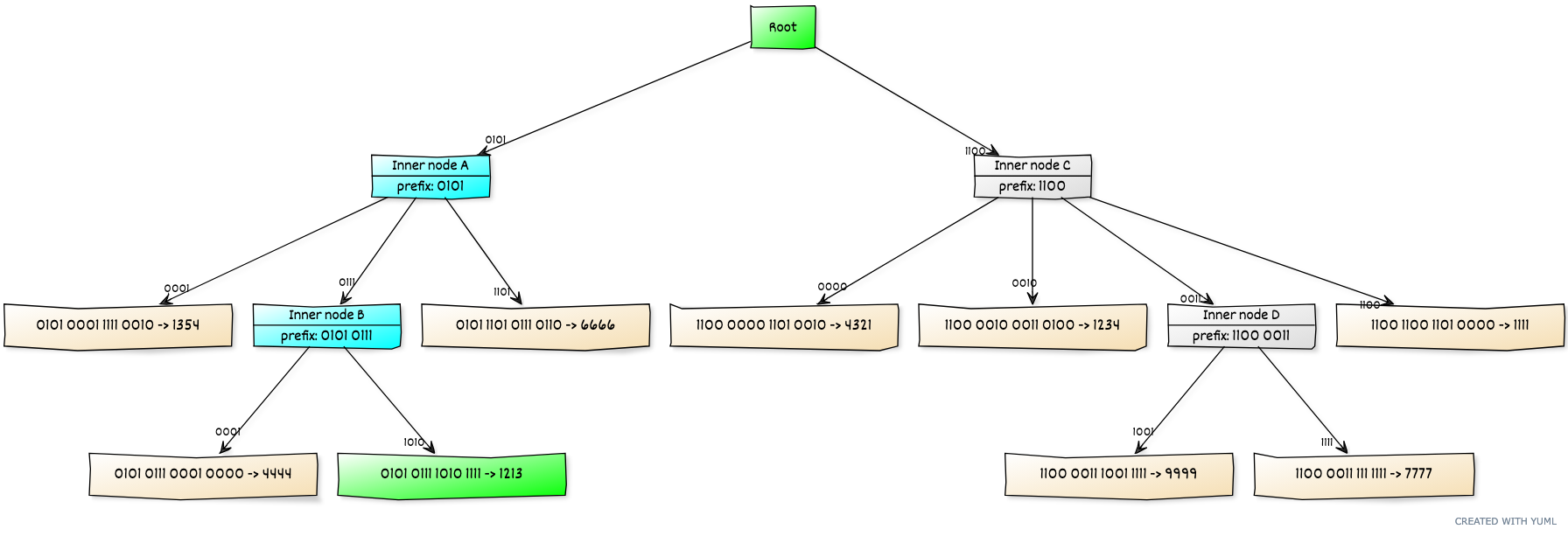
Merkle Patricia Tree

可以理解为把Merkle Tree 从二叉树变成16叉树，再加个Value字段

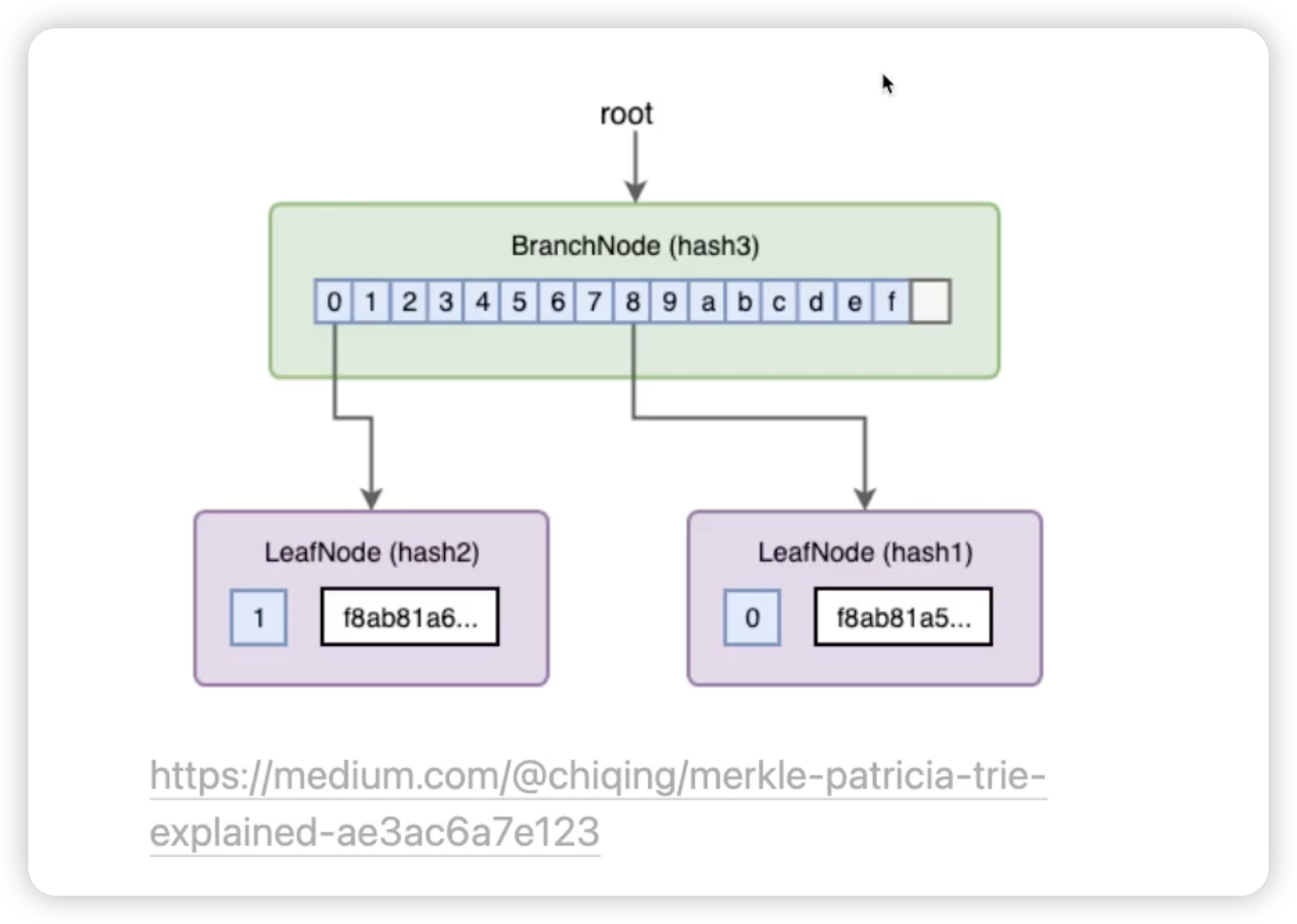
把所有的node存到key-value DB里面，以hash（node)作为key
把node里面叶子的指针替换为叶子的hash(node)

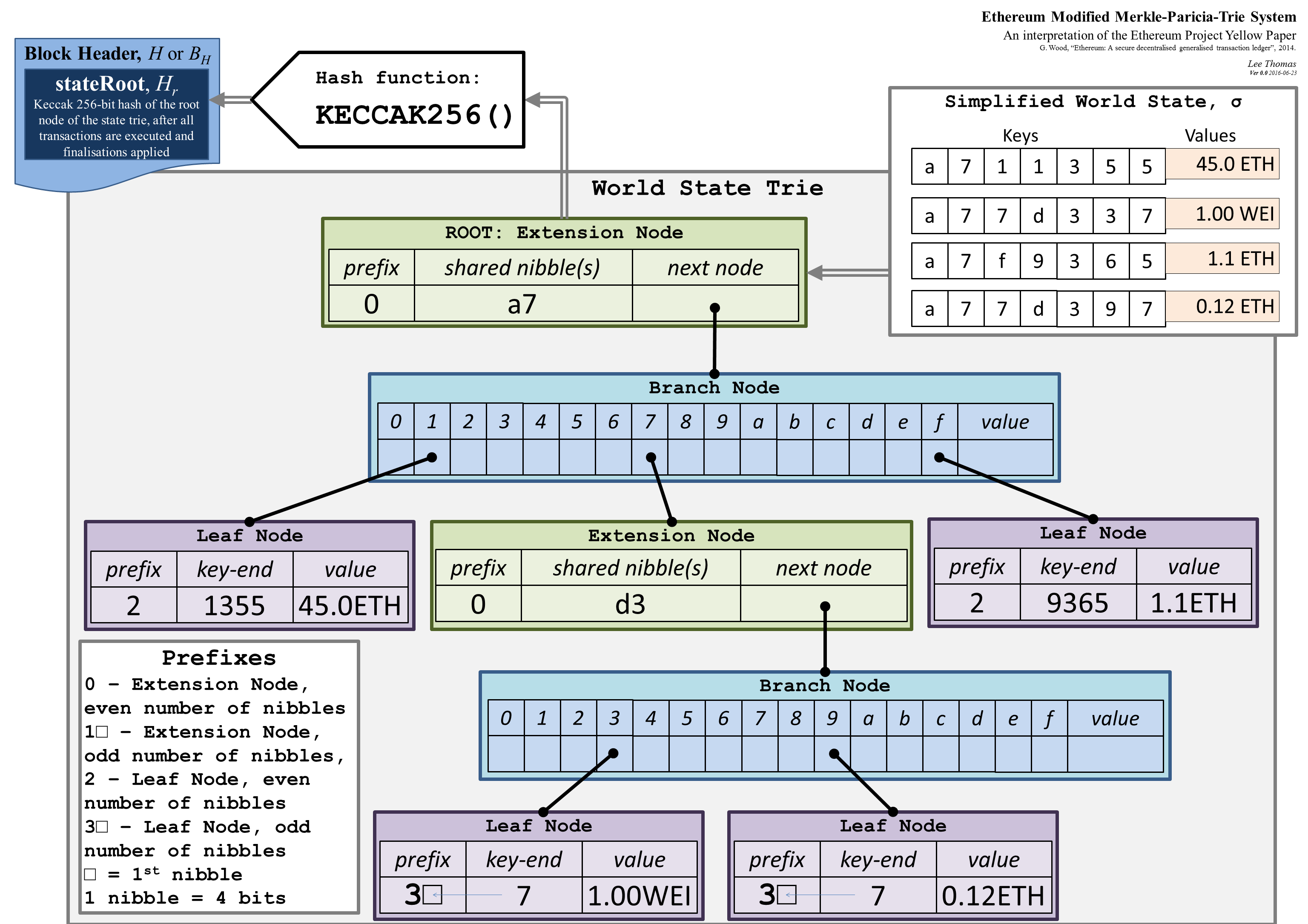
key-end 对应的是图中左侧数据被压缩的ulus

Merkle Patrizia Tree 的问题

索引时，需要$O(log{16}N)$次DB请求，比普通Map的1次DB请求慢很多，时间复杂度$O(K)\rightarrow O(K *log{16}N)$
PoI时，空间复杂度$O(16 * log_{16}N)$, 比普通Merkle Tree的O(log N)慢
改成二叉树，则索引的DB请求次数更多

Rollup的State Tree

Rollup的state Tree 对性能要求高：需要在合约验证Pol
对Map的key- value pairs 排序后建立 Merkle Tree，==讲PoI过程和索引过程分开，索引归索引，Merkle 归Merkle==
1. {Address0: State0, Address1:State1,...} ->
  1. Map索引(有序）：{Address0: Index0, Address1:Index1,...} +
  2. Key-value pairs排序：[(Address0, State0),(Address1, State1),...]
2. 举例：{Alice :50, Bob:100, Charlie:150,...} ->
  1. Map:{Alice:0, Bob:6, Charlie:12}
  2. Key-value pairs ：{Alice: 50, Bob:100, Charlie:150}
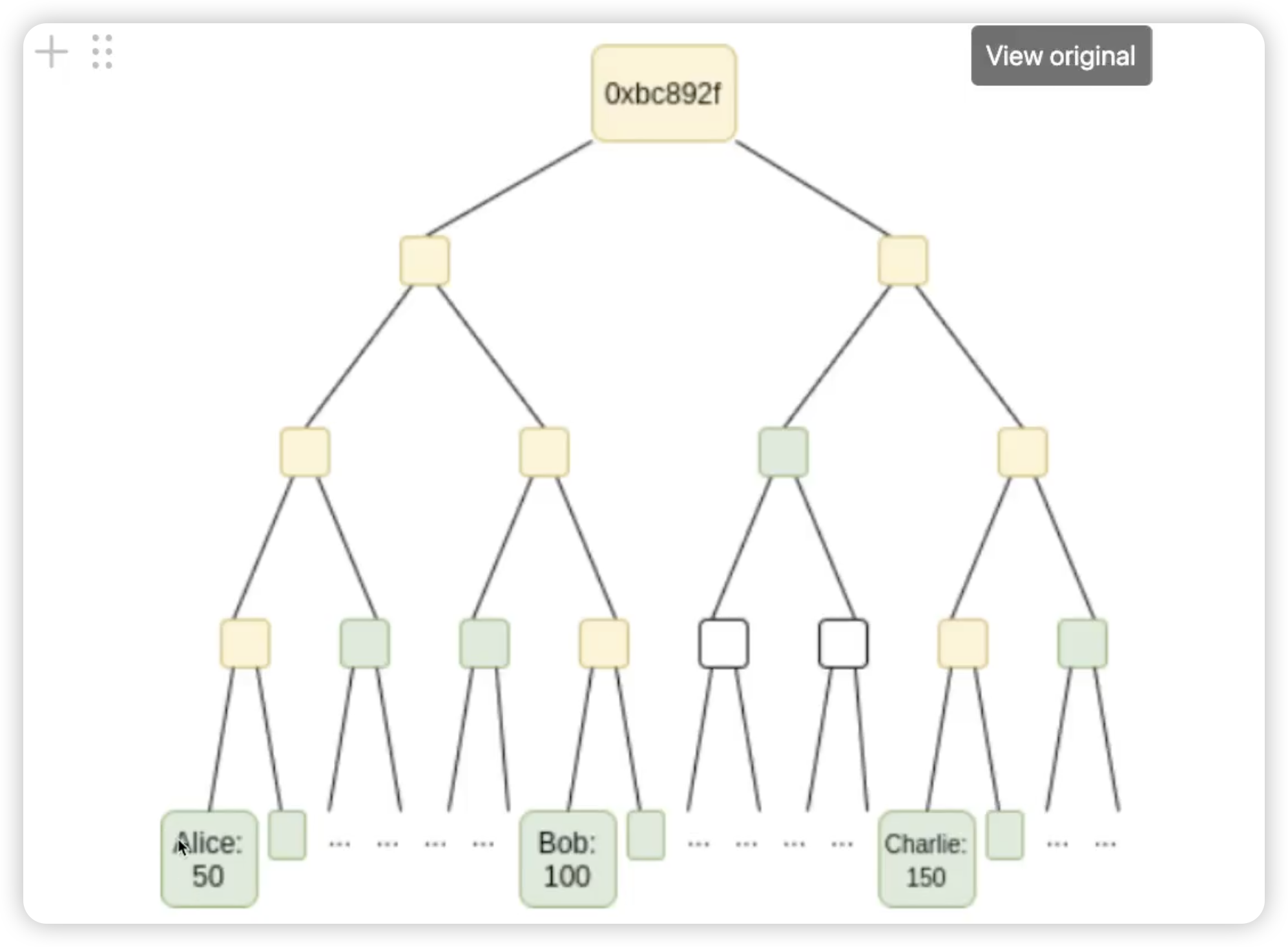
  此时Alice 对应的数组第0位（Index0），Bob对应数组第6位（Index1），Charlie对应数组12位(Index2)
分析
- Map和PoI的数据结构分离，互不影响
- 索引的性能和Map查找一致
- 16叉树回归2叉树，PoI性能等同于Merkle Tree

Verkle Tree

需求：Stateless Client
1. 节点不保存完整的State Tree，只获取需要的State 来验证Block
2. Portal Network
3. 对State Tree的 PoI更高的性能要求
回顾Data Availability 的 KZG commitment
1. 每个leaf 都是polynomial(多项式)上的点
2. constant size proof，和leaf数量无关

Verkel Tree 多叉树

空间复杂度从Merkle Partricia Tree的$O(16 * log_{16}N)$、merkle Tree的O（log N），提升为O(log_16 N)

Merkle Tree的其他用例：AirDrop

Conclusion

这篇文章内容含量有点儿多，包括了CT的介绍，CT所使用的数据结构Merkle tree，Merkle Tree的原理，Merkle Tree 的验证，Merkle tree的替代，关于Fork Consistency还是有一些不太明白（主要是加入客户端、客户端缓存的STH表头信息等），但解决Fork consistency的思想还是比较清楚的。

KTurnura / paper-notes

Fork Consistency：The use of Merkle Tree in untrusted systems #22

证书