search

LayerXcom / safety-oracle

MIT License
1 stars 1 forks source link

readme

Safety Oracle

This document is a comprehensive summary of safety oracles, finality detection mechanisms of CBC Casper.
(See this slide for a general introduction of CBC Casper and this post about finality detection in CBC Casper.)
We introduce various existing proposals on safety oracles, describe the algorithms, and compare them. The goal of this project is here.

Table of Contents

Definitions

t: Byzantine (or equivocation) fault tolerance.

CAN_ESTIMATE: The candidate estimate.

ADV_ESTIMATE: The estimate that the adversary wants to finalize.

MessageDAG

MessageDAG is a DAG (directed acyclic graph) of messages where edges are directed from a message to the messages in its justification.

Message types

Example

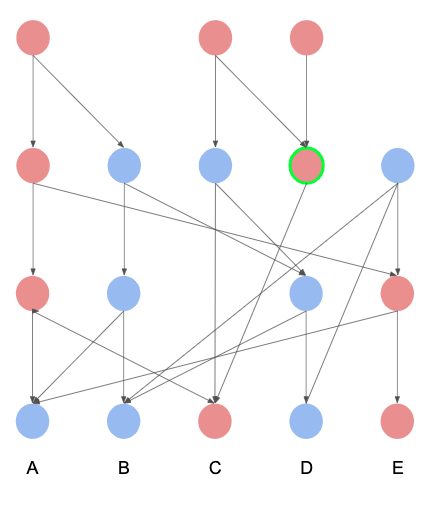
Notations

V: The number of validators.

M: The number of messages(vertices) in the MessageDAG.

J: The number of edges in the MessageDAG.

In practice, we can assume that V <= M <= J <= MV.

Lobbying Graph

We construct a lobbying graph G(V, E) as follows.

  1. Let V be a set of validators that estimates CAN_ESTIMATE in their latest message and G be a directed graph with a set of vertices V.

  2. An edge is directed from v1 to v2 that satisfies the following conditions.

    • v1 ≠ v2
    • The justification of the latest message of v1 includes a message of v2
    • The justification of the latest message of v2 includes a message of v1
    • The latest message of v2 in the justification of the latest message of v1 does not conflict with CAN_ESTIMATE
    • The latest message of v1 in the justification of the latest message of v2 does not conflict with CAN_ESTIMATE
    • No message conflicts with CAN_ESTIMATE among the messages of v2 that v1 have not seen yet
    • No message conflicts with CAN_ESTIMATE among the messages of v1 that v2 have not seen yet

Example

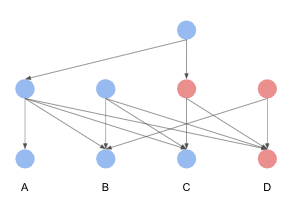
The lobbying graph constructed from the above MessageDAG is:

Complexity

Construct Update for a new message
Time O(V^2 + VM) O(V)
Space O(V^2) -

In 2, it requires O(1) time on average to check if the justification of a message includes another validator using a hash table. For each validator, it requires O(M) to get the latest messages of the other validators (to check if the latest message conflicts with CAN_ESTIMATE). Therefore, the overall complexity is O(VM).

However, if you keep the lobbying graph and update every time you receive a message, this process can be improved. It only requires O(V) to update the graph in receiving a message because the number of newly connected edges in the MessageDAG is at most V for a message.

The space complexity is O(V^2) because E is O(V^2) for any graph. Of course, the space complexity of the MessageDAG is O(J). However, a validator must always have it, so we do not consider it's space in safety oracles.

Clique Oracle

The clique oracle is a family of algorithms to find a clique of validators.

2-round Clique Oracle

This oracle is the most naive clique oracle which tries to find a maximal weight clique.

Algorithm

  1. Construct the lobbying graph or get it.

  2. Convert the lobbying graph to an undirected graph by connecting vertices (validators) connected bidirectionally.

  3. Find the maximum weighted clique C of G in exponential time.

  4. Byzantine fault tolerance is t = ceil(W(C) - W(V)/2) - 1. (q > n/2 + t)

See: https://en.wikipedia.org/wiki/Clique_problem#Finding_maximum_cliques_in_arbitrary_graphs

Metrics

From scratch For a new message
Time complexity exponential exponential
Space complexity - -

Finding a clique requires O*(2^V) time. Even the fastest algorithm requires O*(1.1888^V). ( O*(f(k)) = O(f(k) poly(x)) )

Why q > n/2 + t?

q > n/2 + t, so t < q - n/2.

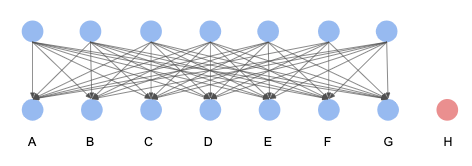
In the above case, n = 8, q = 7, t < 7 - 8/2 = 3.

This result means that up to t-1=2 equivocation failures can be tolerated.

2 equivocating validators:

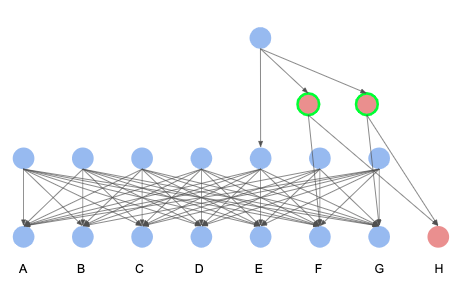
3 equivocating validators:

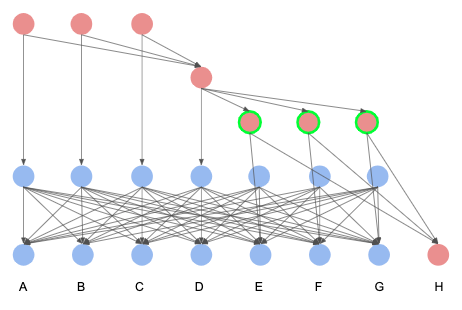
Therefore, the clique oracle fault tolerant threshold formula is not q > n/2 + t/2.

When satisfying the formula q > n/2 + t/2, t < 2q - n = 14 - 8 = 6.

Turán Oracle

Turán theorem

This theorem gives a lower bound on the size of a clique in graphs. If a graph has many edges, it contains a large clique.

Let G be any graph with n vertices, such that G is K_{r+1}-free graph that does not contain (r+1)-vertex clique.

The upper bound of the number of edges is

.

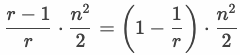Let E be the set of edges in G.

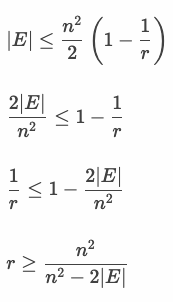
r is a lower bound on the size of a clique in graphs with n vertices and |E| edges.

Algorithm

  1. Construct the lobbying graph or get it.

  2. Convert the lobbying graph to an undirected graph by connecting edges (validators) connected bidirectionally.

  3. Calculate the minimum size of the maximum weighted clique using the above formula in O(1) time.

  4. Calculate the maximum weighted clique C.

  5. t = ceil(W(C) - W(V)/2) - 1. (q > n/2 + t)

Metrics

From scratch For a new message
Time complexity O(V^2 + VM) O(1)
Space complexity O(V^2) -

Finality Inspector

Simple Inspector

The Simple Inspector is a generalization of 2-round clique oracle.

Algorithm

  1. Construct the lobbying graph G or get it.
  2. Let q > n/2 + t.
  3. Compute outdegree of vertices in G.
  4. C = V
  5. Look for the vertice with outdegree of q or less in C, remove it from C, and update the outdegree counters.
  6. Repeat 5.
  7. If W(C) >= q, the property is considered finalized.

Metrics

From scratch For a new message
Time complexity O(V^2 + VM) O(V^2)
Space complexity O(V^2) -

Inspector

Algorithm

See: https://hackingresear.ch/cbc-inspector/

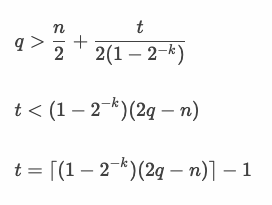
For some q (<= V), the algorithm needs to find the maximum t.

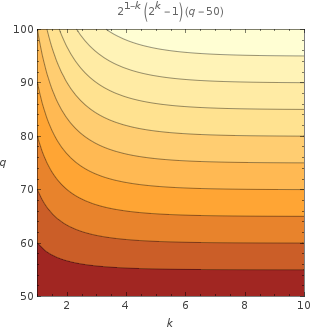
This image is the contour plot about t where n = 100.

Computing the levels takes V times at worst, and the computation runs in O(J) time.

Therefore the total time complexity is O(V * V * J) = O(V^2J).

Metrics

From scratch For a new message
Time complexity O(V^2J) O(V^2J)
Space complexity O(J) -

Adversary Oracle

Adversary oracles is a family of algorithms based on the simulation of an adversary.

Adversary Oracle (straightforward)

Ref: ethereum/cbc-casper

This oracle is a simple simulation-based algorithm.

Algorithm

  1. Construct the lobbying graph or get it.

  2. From view, we can see that there are validators from which the estimate of the latest messages is CAN_ESTIMATE or ADV_ESTIMATE or unknown.

  3. If the estimate is unknown, we assume that it is ADV_ESTIMATE in O(V^2) time.

    C = set()
for v in V:
    if v in view.latest_messages and view.latest_messages[v].estimate == CAN_ESTIMATE:
        C.add(v)

  4. Build viewables with the following pseudocode in O(V^2) time.

    for v1 in V:
    for v2 in V:
        justification = view.latest_messages[v1].justification
        if v2 not in justification:
            viewables[v1][v2] = ADV_ESTIMATE
        elif (there is a v2 message that estimate ADV_ESTIMATE and have seen from v1):
            viewables[v1][v2] = ADV_ESTIMATE
        else:
            viewables[v1][v2] = (message estimate that the hash is justification[v2])

  5. Assume that all validator estimates that may change from CAN_ESTIMATE to ADV_ESTIMATE are ADV_ESTIMATE.

    progress_mode = True
while progress_mode:
    progress_mode = False

    to_remove = set()
    fault_tolerance = -1
    for v in C:
        can_weight = sum(v2.weight for v2 in viewables[v] if viewables[v2] == CAN_ESTIMATE and v2 in C))
        adv_weight = sum(v2.weight for v2 in viewables[v] if viewables[v2] == ADV_ESTIMATE or v2 not in C))

        if can_weight <= adv_weight:
            to_remove.add(v)
            progress_mode = True
        else:
            if fault_tolerance == -1:
                fault_tolerance = can_weight - adv_weight
            fault_tolerance = ceil(min(fault_tolerance, can_weight - adv_weight) / 2) - 1

    C.difference_update(to_remove)

if (total weight of CAN_ESTIMATE) > (total weight of ADV_ESTIMATE):
    the property is finalized

  6. If (total weight of CAN_ESTIMATE) > (total weight of ADV_ESTIMATE) is finally satisfied, the property is finalized.

  7. t = ceil(min_{v in C}{(can_weight of v) - (adv_weight of v)} / 2) - 1.

N.B. The original ethereum/casper's fault tolerance t is the minimum validator weight in C, but we think that it is min{can_weight - adv_weight}/2

Metrics

From scratch For a new message
Time complexity O(V^3 + VM) O(V^3)
Space complexity O(V^2) -

Adversary Oracle with Priority Queue (WIP)

We improve the above algorithm using a priority queue.

Metrics

From scratch For a new message
Time complexity O(V^2 + VM) O(V^2)
Space complexity O(V^2) -

Ideal Oracle

We can construct an oracle which is equivalent to the necessary and sufficient conditions of finality by simulating all the possible state transitions. If the consensus value does not change in any reachable future states, the property is considered finalized. Although this is the best about the completeness, it would be extraordinary inefficient, so we omit here about the detail.

Comparison

Complexity

Detection from scratch

Clique Oracle Turán Oracle Simple Inspector Inspector Adversary Oracle Adversary Oracle with Priority Queue
Time exponential O(V^2 + VM) O(V^2 + VM) O(V^2J) O(V^3 + VM) O(V^2 + VM)
Space - O(V^2) O(V^2) O(J) O(V^2) O(V^2)

Detection for a new message

Clique Oracle Turán Oracle Simple Inspector Inspector Adversary Oracle Adversary Oracle with Priority Queue
Time exponential O(1) O(V^2) O(V^2J) O(V^3) O(V^2)

Fault tolerance and quorum

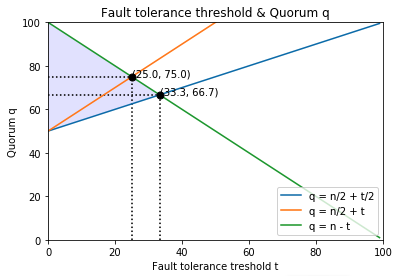
This image shows the relationship between Byzantine fault tolerance (for both safety and liveness) and the quorum of safety oracles. The q = n - t line is the maximum number of honest validators. For liveness, the quorum must be less than or equal to this line. The safety oracles whose quorum condition is q > n/2 + t achieve n/4 Byzantine fault tolerance. On the other hand, safety oracles that use q > n/2 + t/2 achieve n/3.

Example 1

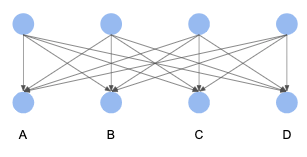
Clique Oracle Turán Oracle Simple Inspector Inspector Adversary Oracle
t 1 1 1 1 1

Example 2

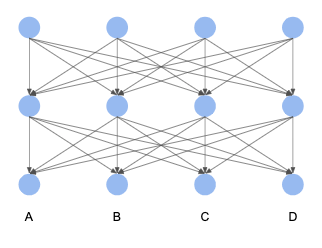
Clique Oracle Turán Oracle Simple Inspector Inspector Adversary Oracle
t 1 1 1 2 1

In this sample, the Inspector fault tolerance threshold is:

t = ceil((1-2^(-2))(2q - n)) - 1 = ceil((3/4)*(8-4)) - 1 = 2.

Example 3

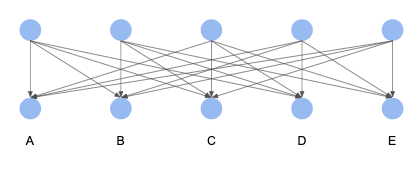
Clique Oracle Turán Oracle Simple Inspector Inspector Adversary Oracle
t N/A N/A 1 1 1

In this case, the clique oracle and the Turán oracle have not yet detected finality.

{A,B,C,D,E} is the quorum set and q = 4, so fault tolerance threshold of the Simple Inspector and the Inspector t = ceil(q - n/2) - 1 = ceil(4 - 5/2) - 1 = 1.

The t of the adversary oracle is also ceil((4-1)/2) - 1 = 1.

Example 4

Clique Oracle Turán Oracle Simple Inspector Inspector Adversary Oracle
t 2 N/A 2 2 2

In the Turán oracle, n^2/(n^2-2|E|) = 8^2 / (8^2 - 7*6) = 64/22 = 2.9... < n/2.

Conclusion