MatchingMarkets

A python toolbox for simulation of matching markets in economics.

The toolbox uses generic abstractions and python lambdas to produce simulations of general matching markets. Examples of matchings markets are organ exchanges, school/student assignment or matching goods and individuals in a barter economy. These markets can last one period, or can evolve over many time periods. Here is an example of a graph produced with the package of a market evolving over many periods:

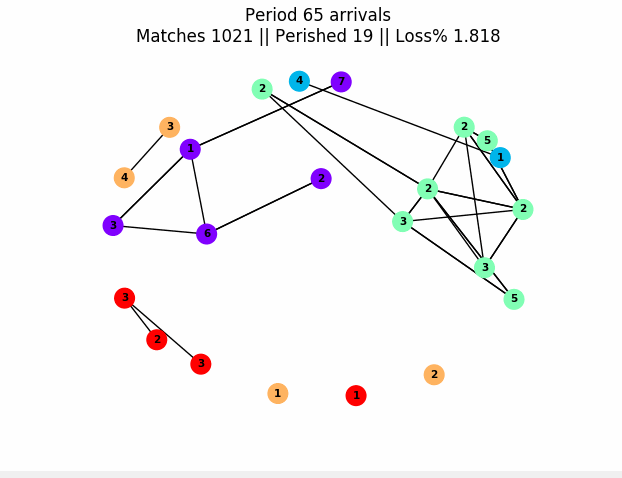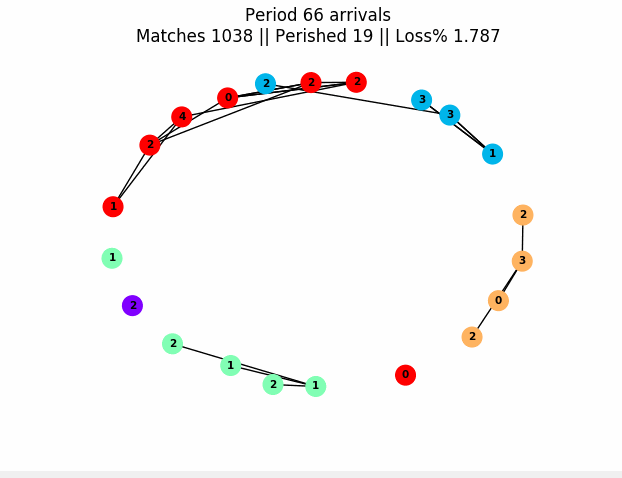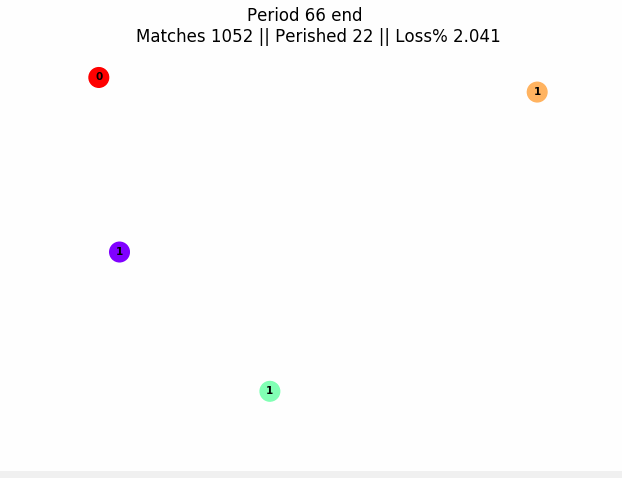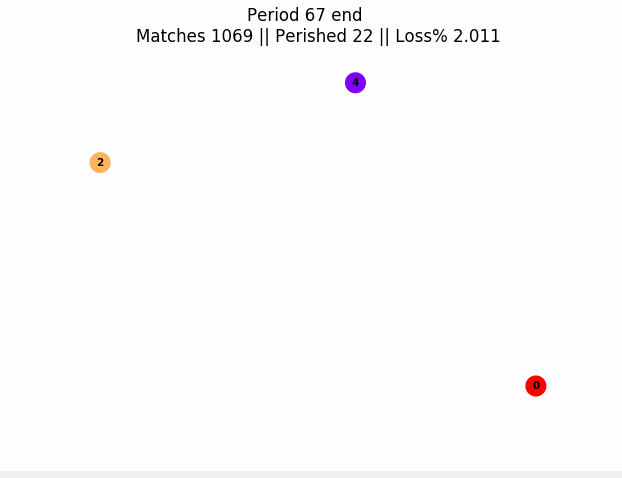
In this graph, nodes are people and node color is their "type" (think patient or donor blood type in organ transplants). The number on a node is periods of life left before death if not matched. An edge means they are compatible (it can be weighed if there's risk of failure). Edges get highlighted red before matches. In this simulation, only people of the same type can be compatible, and we naively match two compatible individuals at random. Our timing decision rule here is to naively try to match everyone each period.

The figure can be produced with this code:

import matchingmarkets as mm
import numpy.random as rng

newsim = mm.simulation(time_per_run=100, max_agents=5000,
                       arrival_rate=15, average_success_prob=lambda: 0.3,
                       typeGenerator=rng.randint,
                       compatFct=mm.stochastic_neighborSameType,
                       crit_input=3, numTypes=5)

# Make sure matplotlib is __not__ inline for this
newsim.graph(plot_time=0.8)

Dependencies

MatchingMarkets.py aims to be "batteries included". If you use the Anaconda distribution with python 3, you should have no problems using the package.

Formally, it requires Python 3.6+, Numpy/scipy, NetworkX, matplotlib with qt5agg backend (for interactive graph plotting) This backend can be changed manually in "Markets.py" A PuLP installation is included by default in matchingmarkets/algorithms/pulp for kidney solvers. This uses the COIN-OR cbc solver by default and can be changed to Gurobi, CPLEX or other compatible solvers manually

Included algorithms

• Random pairwise match (default)

• Top Trading cycle

• Gale-Shapley deferred acceptance algorithm

• Serial dictatorship (serial ordering is user definable with lambda input)

• Max weight matching (Based on blossom algorithm)

• Max cardinality matching

• Modern kidney solvers are not functional yet.

Market Generating

It can be useful to try out a few settings on generators and visualize the output to see if the simuation is what you want. The current suite of generators is in this file. Currently we have:

• Random or deterministic assignment of one or multiple abstract types

• Blood types (for organ transplants)

• It's easy to write a lambda and pass it in the typeGenerator attribute in a mm.simulation object. The lambda should respect the format of generator functions.

More important is the function defining match compatibility based on types of agents. This is in the same file as above. Using abstract types and cutoff values for the RNG, you can simulate many classic matching problems easily. It is also easy to write a lambda which simulates the compatibility you desire as long as it respects the form f(sourceAgent, receivingAgent, cutoff=1) -> float in [0,1] where the result is the match success probability, and cutoff is an optional parameter usually used in an RNG.

Use

Please refer to the tutorial notebook for more in depth instructions.

Download the package, change directory to the one containing it in your python console, and import matchingmarkets as mm.

Intended use is through the simulation object, as follows:

newsim = mm.simulation(
                      # Simulation parameters here
                      )
newsim.run()

#prints output of a simulation
newsim.stats()

out[5]:
Simulation Results
1  periods
50  runs
Stat      value  (std dev)
==================================
Welfare:   50.04 ( 6.7675 )
matches:   50.04  ( 6.7675 )
perished:  0.0  ( 0.0000 )
loss%:     0.0000  ( 0.0000 )

One way to get as much information about your simulation as possible is to run it with the verbose flag on, and plot a few periods:

newsim.verbose = True
newsim.graph(period=10)
# This will print all relevant information to console, and graph the output

The simulation class has many attributes to simulate static (single period) or dynamic (multi-period) matching markets. When creating the simulation class, you can pass the following parameters:

      runs: int
        number of trials when runs

      time_per_run: int
          number of time periods in a run

       max_agents: int
          maximum number of agents over a run overall

       logAllData: bool
          log every single period on every iteration
          Takes much longer, but outputs pretty plots in the stats() function
          if false, only logs final results on each run

        arrival_rate: int
            average number of new agents per period
            the lambda in a poisson distribution

        average_success_prob: f() -> float[0,1]
            cutoff value passed in neighborfct
            1 - pr(failure of match) for average of mrkt

        algorithm: f(list<agent>) -> dict{agent.name : agent.name}
            Matching Algorithm
            takes current agents in market as input
            returns a list of matches
            see algorithms.py for details

        arrival_fct: fct(float) -> int
            function that returns number of arrival this period
            poisson distribution draw by default

        crit_input:int
            input in time_to_crit, usually param in a rng fct

        discount: fct() -> [0,1]
            function generating agent discount rate

        matchUtilFct: fct(agent1, agent2, float) -> float
            returns utility for agent1 of matching to agent2

        metaAlgorithm: f(market, algorithm, **kwargs)
                            -> dict{agent.name : agent.name}
            Algorithm responsible for timing decisions
            Decides when to match, and who participates
            in the matching algorithm

        metaParams: dict{string: value}
            kwargs passed into the metaAlgorithm
            This can then be passed into the Algorithm

        neighborFct: fct(agent1, agent2, float) -> float
            rng function returning agents who are
            compatible matches based on input
            float parameter is a cutoff value for rng

        numTypes: int
            input in typeGenerator
            usually # of types

        utilityFctInput: float
            input for matchUtilFct (usually rng cutoff value)

        selfMatch: bool
            true if an agent can match himself
            ex: House market
            false if an agent has to match another
            ex: marriage market

        time_to_crit: fct() -> int
            function generating agent time to crit

        typeGenerator: fct(int) -> int
            function generating agent type

        verbose: bool
            print on relevant actions in update

TODO:

replace plotting animations with Celluloid