search

eboigne / PyTV-4D

Python routines to compute the Total Variation (TV) of 2D, 3D and 4D images on CPU & GPU. Compatible with proximal algorithms (ADMM, Chambolle & Pock, ...)
GNU General Public License v3.0
32 stars 6 forks source link
admm-algorithm chambolle-pock computed-tomography proximal-operators tomography total-variation total-variation-loss total-variation-minimization totalvariation

readme

PyTV-4D

A set of Python routines to compute the Total Variation (TV) of 2D, 3D and 4D (3D and time) images on CPU & GPU, in application to image denoizing and iterative Computed Tomography (CT) reconstructions. The time-resolved capabilities are useful for dynamic CT or motion artifact corrections. This is the code used in this article.

Current features

Installation

CPU & GPU

Conda [Recommended]

First, install PyTorch (version at least 1.5.0) following the guidelines on the official website. Make sure to install the correct version for your setup to enable GPU computations.

Then, the PyTV-4D files can be installed as a package using anaconda:

conda install -c eboigne pytv

Manual installation

PyTV-4D can also be installed manually with (dependencies need to be set properly):

python setup.py install

CPU Only

For a quick installation running the CPU routines only, install numpy and PyTV-4D using anaconda, skipping the PyTorch dependency for PyTV-4D:

conda install numpy && conda install --no-deps -c eboigne pytv

Testing

Once installed, you can run some basic tests on CPU and GPU:

import pytv

pytv.run_CPU_tests()
pytv.run_GPU_tests()

Note that the tests may fail because of bad rng, so try running it a couple times.

Getting started

See the details below and the getting started Jupyter notebook.

Computing TV and subgradient

Below is a simple example to compute the total variation and sub-gradient on CPU and GPU:

import pytv  
import numpy as np

Nz, M, N = 20, 4, 100 # 4D Image dimensions. M is for time.
np.random.seed(0)
img = np.random.rand(Nz, M, N, N)

tv1, G1 = pytv.tv_CPU.tv_hybrid(img)
tv2, G2 = pytv.tv_GPU.tv_hybrid(img)

print('TV value from CPU: '+str(tv1))
print('TV value from GPU: '+str(tv2))
print('Sub-gradients from CPU and GPU are equal: '+str(np.prod(np.abs(G1-G2)<1e-5)>0))

Output is:

TV value from CPU: 532166.8251801673
TV value from GPU: 532166.8
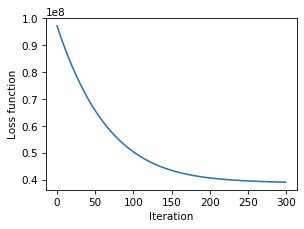
Sub-gradients from CPU and GPU are equal: True

Denoizing an image

A simple example of image denoizing using the total variation. The following loss function is minimized:

where is the current image, is the input noisy image, and is a regularization parameter. Because the TV is not everywhere differentiable, the sub-gradient descent method is used to minimize this loss function:

noise_level = 100
nb_it = 300
regularization = 25
step_size = 5e-3 # If step size is too large, loss function may not decrease at every step

np.random.seed(0)
cameraman_truth = pytv.utils.cameraman() # Open the cameraman's grayscale image
cameraman_truth = np.reshape(cameraman_truth, (1,1,)+cameraman_truth.shape)
cameraman_noisy = cameraman_truth + noise_level * np.random.rand(*cameraman_truth.shape) # Add noise
cameraman_estimate = np.copy(cameraman_noisy)

loss_fct_GD = np.zeros([nb_it,])
for it in range(nb_it): # A simple sub-gradient descent algorithm for image denoising
    tv, G = pytv.tv_GPU.tv_hybrid(cameraman_estimate)
    cameraman_estimate += - step_size * ((cameraman_estimate - cameraman_noisy) + regularization * G)
    loss_fct_GD[it] = 0.5 * np.sum(np.square(cameraman_estimate - cameraman_noisy)) + regularization * tv

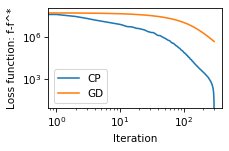
Images of the cameraman Loss function

Accelerated convergence using gradient operators

Because the loss function with total variation is non-smooth, it is challenging the achieve sufficient convergence with the gradient descent algorithm. Instead, the primal-dual algorithm from Chambolle and Pock (https://doi.org/10.1007/s10851-010-0251-1) achieves faster convergence. The ADMM algorithm can also be used. To enable easy implementation of such proximal-based algorithm, the calculations of image gradients are available in PyTV-4D. A simple example is presented below in the case of the denoising of the cameraman image: 

# A simple version of the Chambolle & Pock algorithm for image denoising
# Ref: Chambolle, Antonin, and Thomas Pock. "A first-order primal-dual algorithm for convex problems with applications to imaging." Journal of mathematical imaging and vision 40.1 (2011): 120-145.
sigma_D = 0.5
sigma_A = 1.0
tau = 1 / (8 + 1)

for it in range(nb_it):

    # Dual update
    dual_update_fidelity = (dual_update_fidelity + sigma_A * (cameraman_estimate - cameraman_noisy))/(1.0+sigma_A)
    D_x = pytv.tv_operators_GPU.D_hybrid(cameraman_estimate)
    prox_argument = dual_update_TV + sigma_D * D_x
    dual_update_TV = prox_argument / np.maximum(1.0, np.sqrt(np.sum(prox_argument**2, axis = 1)) / regularization)

    # Primal update
    cameraman_estimate = cameraman_estimate - tau * dual_update_fidelity - tau * pytv.tv_operators_GPU.D_T_hybrid(dual_update_TV)

    # Loss function update
    loss_fct_CP[it] = 0.5 * np.sum(np.square(cameraman_estimate - cameraman_noisy)) + regularization * pytv.tv_operators_GPU.compute_L21_norm(D_x)

Loss function

Functions overview

PyTV-4D provides the following functions:

use_GPU = True

import numpy as np
if use_GPU:
    import pytv.tv_GPU as tv
else:
    import pytv.tv_CPU as tv

Nz, M, N = 20, 4, 100 # 4D Image dimensions. M is for time.
np.random.seed(0)
img = np.random.rand(Nz, M, N, N)

# TV values, and sub-gradient arrays
tv1, G1 = tv.tv_upwind(img)
tv2, G2 = tv.tv_downwind(img)
tv3, G3 = tv.tv_central(img)
tv4, G4 = tv.tv_hybrid(img)
use_GPU = True

import numpy as np
if use_GPU:
    import pytv.tv_operators_GPU as tv
else:
    import pytv.tv_operators_CPU as tv

Nz, N = 10, 100 # Image size 
M = 2 # Time size
reg_time = 2**(-5) # Time regularization (lambda_t)
img = np.random.rand(Nz, M, N, N)

# Discrete gradient: D_img has size (Nz, Nd, M, N, N) where Nd is the number of difference terms
D_img1 = tv.D_upwind(img, reg_time = reg_time)
D_img2 = tv.D_downwind(img, reg_time = reg_time)
D_img3 = tv.D_central(img, reg_time = reg_time)
D_img4 = tv.D_hybrid(img, reg_time = reg_time)

# Transposed discrete gradient: D_T_D_img has size (Nz, M, N, N)
D_T_D_img1 = tv.D_T_upwind(D_img1, reg_time = reg_time)
D_T_D_img2 = tv.D_T_downwind(D_img2, reg_time = reg_time)
D_T_D_img3 = tv.D_T_central(D_img3, reg_time = reg_time)
D_T_D_img4 = tv.D_T_hybrid(D_img4, reg_time = reg_time)

# TV values: obtained by computing the L2,1 norm of the image gradient D(img) 
tv1 = tv.compute_L21_norm(D_img1)
tv2 = tv.compute_L21_norm(D_img2)
tv3 = tv.compute_L21_norm(D_img3)
tv4 = tv.compute_L21_norm(D_img4)

TV definition

TV definition TV discretization

Comments

Cite

Please refer to the following article in your publications if you use PyTV-4D for your research:

@article{boigne2022towards,
author={Boign{\'e}, Emeric and Parkinson, Dilworth Y. and Ihme, Matthias},
journal={{IEEE Transactions on Computational Imaging}},
title={{Towards data-informed motion artifact reduction in quantitative CT using piecewise linear interpolation}},
year={2022},
volume={8},
pages={917-932},
doi={10.1109/TCI.2022.3215096}
}

License

PyTV-4D is open source under the GPLv3 license.

To do