SOAP_GAS

A genetic algorithm to optimise the SOAP descriptor.

Motivation

The Smooth Overlap of Atomic Positions (SOAP) descriptor [1] is a set of mathematical objects that can be used to represents and/or extract information from molecular structures. The SOAP descriptor has been used to build machine learning-based interatomic potentials for a number of materials. More relevant to the SOAP_GAS code, however, is the usage of the SOAP descriptor to predict the functional properties of molecular structures by means of machine learning algorithms.

At its core, the SOAP descriptor can be thought as a representation of the local atomic environments within a certain molecular structure. Said representation is obtained by using a local expansion of a Gaussian smeared atomic density with orthonormal functions based on spherical harmonics and radial basis functions.

In order to obtain a SOAP descriptor, one has to pick one or more atomic species as centre(s) of the local atomic environments and one or more species as the neighbors of the central atom that define said environment. It is not uncommon to use multiple SOAP descriptors, characterised by different choices of centres and neighbors, as they do contain information that might be hidden when simply choosing every atomic species in the molecule as both centre and neighbour.

A number of parameters are needed to define a SOAP descriptor, most prominently:

n_max: The number of radial basis functions
l_max: The maximum degree of the spherical harmonics
cutoff: The spatial extent (in Å) of the local atomic environment
atom_sigma: The standard deviation (in Å) of the Gaussian functions

The choice of these parameters is not straightforward, and it is key to the accuracy and the predictive power of the SOAP descriptor. Physical intuition can provide a starting point, particularly in terms of the choice of cutoff (based on e.g. the extent of the moelcular structures in question), but finding (one of the) best combination(s) of these parameters often requires additional effort. A simple grid search in this 4-parameter space is a possibility, particularly if conducted in a randomised fashion, as the typical search space is simply too vast to be systematically explored. A typical search space would be defined by:
2 < n_max 10
2 < l_max 10
5 cutoff 20 [Å]
0.1 < atom_sigma < 1.5 [Å] The size of the grid obviously depends on the granularity of the variation with respect to each parameter, but typical sizes would ential be around 15,000 combinations.

The computational effort required to assess the performance of a given SOAP descriptor varies according to the size of the dataset, the extent of the moelcular structures in question, and the number of centers and neighbors. In addition, different choices of the above mentioned four parameters will massively impact the resulting dimensionality of the SOAP vector, and thus the computational effort. Even when dealing with very small datasets (e.g. 100 molecules), a randomised grid search is needed to try and identify a sufficiently accurate combination of these SOAP parameters.

In addition, optimising the SOAP parameters for different SOAPS via a randomised grid search at the same time would involve an intractacble number of potential combinations.

The Genetic Algorithm

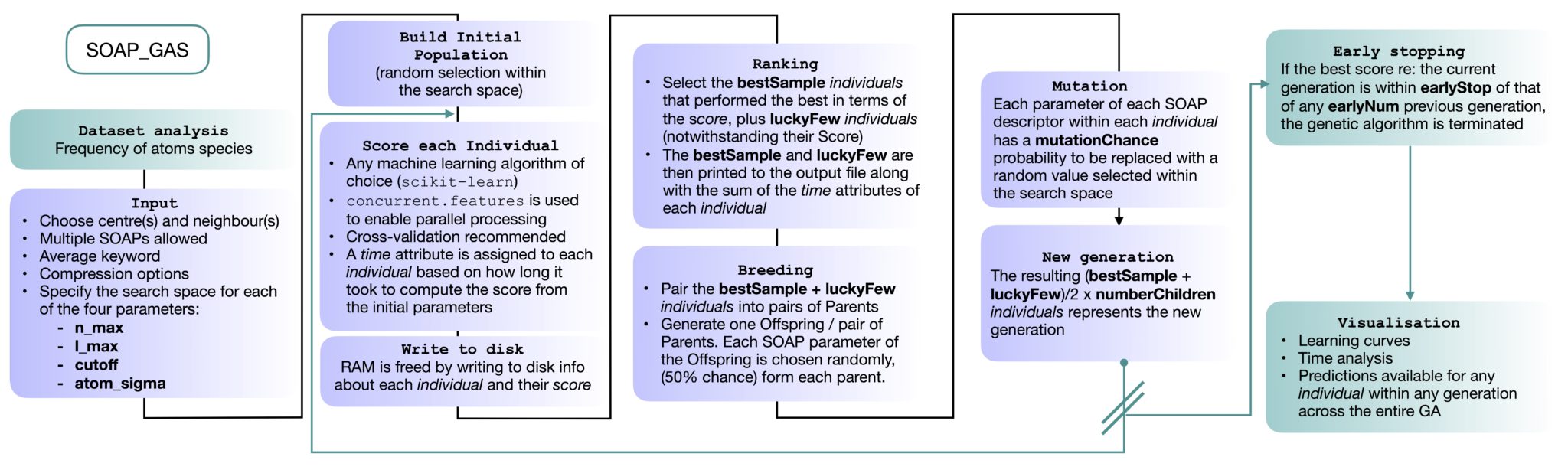
This is an image

The SOAP_GAS code seeks to optimise the SOAP parameters by means of a genetic algorithm, which structure is depicted in the figure below. We start by constructing a so-called Initial Population containing a certain number of Individuals. Each Individual is SOAP descriptor characterised by a randomly selected set of SOAP parameters. For each Invidual within the Initial Population we compute a Score, that is a metric that quantify the accuracy of the Individual in predicting the functional property of interest. The choice of the specific machine learning algorithm used to compute the Score can be easily modified by leveraging widely used Python packages such as scikit-learn. Cross-validation is generally recommeneded (particularly when dealing with small dataset) in orde to ensure the reproducicibility of the Score. When dealing with regression problems, the Score involves the mean squared error (MSE) and the Pearson correlation coefficient (PCC) for both training and test test, whilst for classification problems the Score is based on the Matthews correlation coefficient (MCC).

A certain number (bestSample, see the input reference below) of Individuals is then chosen according to their Score, together with a usually smaller number (luckyFew, see the input reference below) of Individuals notwithstanding their Score. With this selection, we perform the so-called Breeding, by randomly picking pairs of Individuals (hence bestSample + luckyFew needs to be an even number) as Parents. The resulting Offspring of each pair of Parents is a SOAP descriptor where each parameter has been randomly picked by one of the two Parents (with a 50\% chance). We then proceed to apply some Mutations: each SOAP parameter within each Offspring has a certain probability (mutationChance, see the input reference below) to be changed into a randomly picked value (within the boundaries for that specific SOAP parameter). Note that the resulting Population Size [(bestSample+luckyFew)/2) x numberChildren)] is identical to the size of the Initial Population.

Also note that in order to free RAM, information about each Individual is written to disk in an individual class that contains the SOAP parameters, the full SOAP vector, the target values of the whole database, the Score and each of the train/test splits used for the cross validation relative to that particular Score.

Features

Regression as well as classification capabilities
Full control of the search space
Full control of the genetic algorithm parameters, including early stopping criteria
Parallelisation enabled via concurrent.futures
Heterogeneous datasets containing different moelcules with different numbers of atomic species can be considered via the average keyword (see Ref. [1])
3D molecular models of crystals, liquids or amorphous systems can also be considered
Compressed SOAP descriptors can be used to reduce the dimensionality of the descriptors (and thus the computational effort), see Ref. [2].
Simultaneous optimisation of the SOAP parameters for different SOAP descriptors at the same time

Installation

The SOAP_GAS code is written in Python (3.x).

Pre-requisites

GCC (4.9 or higher)
Blas and Lapack. Most of our builds have been tested with OpenBLAS
SciPy. Most of our builds have been tested with SciPy-bundle/2020.11
ase. Tested with ase/3.22.1
Scikit-learn. Tested with scikit-learn/1.0.2

Installation workflow

Get the SOAP_GAS code: https://github.com/gcsosso/SOAP_GAS.git
The required packages can be installed using the pipenv package. This can be installed using: pip install pipenv
Install the required packages: pipenv install Pipfile
pipenv shell activates the environment and the code can be run within this environment.
(optional) If you want to use the usage_example.ipynb notebook, the following command is required to be able to use the pipenv shell in the notebook: python -m ipykernel install --user --name=my-virtualenv-name Note that there are compatibility issues with the version of tensorflow installed using the pipfile and Apple M1 or M2 chips. If you have a machine with one of these chips you will have to manually install the packages listed in the Pipfile.

Input files

input.py: input parameters, see the Input Reference below
database.csv: name of each molecular structure and value of the target property. e.g.
```
Name,Target
acemetacin,310.0
acetaminophen,299.0
bicalutamide,323.0
```
xyz: directory containing an .xyz file for each molecular structure specified in database.csv, e.g. acemetacin.xyz, acetaminophen.xyz, etc.

Selecting centres and neighbors

The choice of which atomic species are to be selected as centres and neighbors for the SOAP descriptor is left to the user. The average keyword within the SOAP descriptor can be used to treat all the neighbors of a given centre agnostically as the same atom type, which results in SOAP vectors of the same dimensionality even across heterogeneous dataset containing different molecules or even different number of different molecules in a given molecular structure. The atomicStats.py script can be used in an interactive fashion (simply as python atomicStats.py) to analyse a dataset of N molecular structures and gain information about the frequency by which a given atomic specie is present within the dataset. The input files are specified above. A typical output would look like:

The atoms present in your dataset are (excluding H): {'H', 'C', 'N', 'S', 'CL', 'O', 'F', 'P'}
The atom counts are: {'H': 2552, 'C': 2161, 'O': 419, 'N': 232, 'S': 39, 'CL': 38, 'F': 31, 'P': 1}
The number of molecules that contain each atom are: {'H': 131, 'C': 131, 'O': 127, 'N': 92, 'S': 30, 'CL': 27, 'F': 13, 'P': 1}
The total number of molecules in the dataframe is: 131
What is the maximum number of atoms for the possible centre/neighbour sets? (Enter an int between 1 and 8): 4
Which atoms (if any) would you like to drop? Please seperate them by spaces
C
The combinations that you could use as centre/neighbour atoms are: [('H',), ('H', 'N'), ('H', 'S'), ('H', 'CL'), ('H', 'O'), ('H', 'F'), ('H', 'P'), ('N', 'O'), ('H', 'N', 'S'), ('H', 'N', 'CL'), ('H', 'N', 'O'), ('H', 'N', 'F'), ('H', 'N', 'P'), ('H', 'S', 'CL'), ('H', 'S', 'O'), ('H', 'S', 'F'), ('H', 'S', 'P'), ('H', 'CL', 'O'), ('H', 'CL', 'F'), ('H', 'CL', 'P'), ('H', 'O', 'F'), ('H', 'O', 'P'), ('H', 'F', 'P'), ('N', 'S', 'O'), ('N', 'CL', 'O'), ('N', 'O', 'F'), ('N', 'O', 'P'), ('H', 'N', 'S', 'CL'), ('H', 'N', 'S', 'O'), ('H', 'N', 'S', 'F'), ('H', 'N', 'S', 'P'), ('H', 'N', 'CL', 'O'), ('H', 'N', 'CL', 'F'), ('H', 'N', 'CL', 'P'), ('H', 'N', 'O', 'F'), ('H', 'N', 'O', 'P'), ('H', 'N', 'F', 'P'), ('H', 'S', 'CL', 'O'), ('H', 'S', 'CL', 'F'), ('H', 'S', 'CL', 'P'), ('H', 'S', 'O', 'F'), ('H', 'S', 'O', 'P'), ('H', 'S', 'F', 'P'), ('H', 'CL', 'O', 'F'), ('H', 'CL', 'O', 'P'), ('H', 'CL', 'F', 'P'), ('H', 'O', 'F', 'P'), ('N', 'S', 'CL', 'O'), ('N', 'S', 'O', 'F'), ('N', 'S', 'O', 'P'), ('N', 'CL', 'O', 'F'), ('N', 'CL', 'O', 'P'), ('N', 'O', 'F', 'P')]

Running the genetic algorithm

python genAlg.py input (note, not python genAlg.py input.py)

Input reference

The input.py file allows the user to specify which SOAP descriptor(S) to be optimised. It also allows to user to specify several parameters to tweak the genetic algorithm specifications. The input file is required to be in the same folder as the genetic algorithm script for it to work.

The specifics of the SOAP descriptor(s) to be optimised are contained in one or more Python dictionaries in the following form:

SOAP_1_dictionary = {'lower' : int ,'upper' : int, 'centres' : '{int(, int, ..., int)}', 'neighbours' : '{(, int, ..., int)}', 'nu_R' : int, 'nu_S': int, 'mutation_chance': float, 'min_cutoff': float, 'max_cutoff' : float, 'min_sigma': float, 'max_sigma': float, 'message_steps':  int}

Search space:

'lower' : (integer) Lower limit for both n_max and l_max
'upper' : (integer) Upper limit for both n_max and l_max
'min_cutoff': (float)
'max_cutoff' : (float)
'min_sigma': (float)
'max_sigma': (float)

Centres and neighbors

'centres' : (list of integers enclosed in {()} brackets) '{int(, int, ..., int)}'. Each integer refers to the atomic number of the atomic species used as centre for that particular SOAP descriptor
'neighbours' : '{(, int, ..., int)}'. Same as 'centres', only this specifies the neighbour atoms instead.

Compression options The different compression options are discussed in Ref. [2].

'nu_R' : int
'nu_S' : int

SOAP example

descDict = {'lower' : 2,'upper' : 6,'centres' : '{8, 7, 6, 1, 16, 17, 9}','neighbours' : '{8, 7, 6, 1, 16, 17, 9}','mu' : 0,'mu_hat': 0, 'nu':2, 'nu_hat':0, 'mutation_chance': 0.15, 'min_cutoff':5, 'max_cutoff' : 10, 'min_sigma':0.1, 'max_sigma':0.5})

mutation_chance: float between 0 and 1. Probability (0-1 implies a zero and a 100% chance, respectively) that each one of the SOAP parameters within each SOAP will mutate from one generation to the next. The same probability is applied independently to each parameter.

Two additional dictionaries are required to run the genetic algorithm. These are population_parameters and history_parameters.

population_parameters

population_parameters = {'best_sample' : int ,'lucky_few' : int, 'population_size' : int, 'number_of_children': int, 'maximise_scores': bool}

best_sample: integer. The number of individuals that produced the best scores, to be picked as parents (together with some luckyFew, see below) for the breeding.
lucky_few: integer. The number of individuals, selected randomly from the population notwithstanding their score, to be picked as parents for he breeding together with the bestSample ones (see above). Note that bestSample+luckyFew cannot be an odd number because the breeding process relies on pairs of individuals.
population_size: integer. Population size, i.e. number of individuals (i.e. number of SOAPs or sets of SOAPs) for each generation. This number does not change across different generations. The following equality has to apply at any time: population_size = numberChildren x (bestSample + luckyFew)/2
number_of_children: integer. The number of individuals generated via the breeding.
maximise_scores: bool. If true, the GA chooses the highest scoring individuals for breeding. If false then the lowest scoring individuals are chosen.

history_parameters

history_parameters = {'early_stop' : float, 'early_number' : int, 'min_generations' : int}

early_stop: float between 0 and 1. Tolerance criterion for any two generations to be considered equally accurate. In conjunction with earlyNum (see below) it determines the early stopping criterion for the GA. E.g., earlyStop=0.04 implies that two generations which best score is within 4% of each other are to be considered as equally accurate.
early_number: integer. Number of equally accurate generations (according to the early_stop threshold, see above) that must be generated in order for the GA to stop. Note that the early_number do not need to be generated consecutively, but at any point along the GA instead.
min_generations: The minimum number of generations that need to elapse before the GA will stop, even if the early_stop criteria is met.

Finally, there are two global parameters that must be specified

descList: list[dict]. A list of the descriptor dictionaries used to calculate the SOAPs
num_gens: integer. The number of generations the GA will run - unless the early stopping criterion (see below) is met.

An example input file is provided in the EXAMPLES folder.

Output files

Backed up outputs
out_.txt
best_.pkl (list of individual classes but no vector and only for the best ones / generation) . learning curves and stuff
history_.pkl (list of list of individual classes / generation)-> this can be massive!

Workflow

atomicStats.py: returns information about the frequency by which a given atomic species is contained within the dataset
genAlg.py : optimises the SOAP descriptor parameters for one or multiple SOAPs
gasVisual.ipynb : visualization of the key results within a Jupyter Notebook

Examples

Optimise the SOAP parameters of a C-C SOAP, with no compression:


SOAP_CC = {'lower' : 2,'upper' : 10,'centres' : '{6}','neighbours' : '{6}','nu_S' : 0,'nu_R': 0, 'mutationChance': 0.15, 'min_cutoff':5, 'max_cutoff' : 20, 'min_sigma':0.1, 'max_sigma':1.5, 'message_steps':0}

population_parameters = {'best_sample': 6, lucky_few': 2, 'population_size': 20, 'number_of_children': 5, 'maximise_scores': False}

history_parameters = {'early_stop': 0.03, 'early_number': 3, 'min_generations': 5} descList = [SOAP_CC] num_gens = 20


* Optimise the SOAP parameters of two SOAP descriptors at the same time, using compression:

SOAP_C_all = {'lower' : 2,'upper' : 10,'centres' : '{6}','neighbours' : '{6, 15, 53, 7, 35, 1, 8, 17, 16, 9}','nu_S' : 0,'nu_R': 0, 'mutationChance': 0.15, 'min_cutoff':5, 'max_cutoff' : 20, 'min_sigma':0.1, 'max_sigma':1.5, 'message_steps':0}

SOAP_H_all = {'lower' : 2,'upper' : 10,'centres' : '{1}','neighbours' : '{6, 15, 53, 7, 35, 1, 8, 17, 16, 9}','nu_S' : 0,'nu_R': 0, 'mutationChance': 0.15, 'min_cutoff':5, 'max_cutoff' : 20, 'min_sigma':0.1, 'max_sigma':1.5, 'message_steps':0}