BezierKit

BezierKit is a comprehensive Bezier Path library written in Swift.

Warning! Prerelease software!
Features
Installation
Usage
License

Warning! Prerelease software!

Please note that BezierKit is currently pre-release software. Its releases follow semantic versioning which means that until it reaches 1.0 status the API may not be stable or backwards compatible.

Features

[x] Constructs linear (line segment), quadratic, and cubic Bézier curves
[x] Draws curves via CoreGraphics
[x] Determines positions, derivatives, and normals along curves
[x] Lengths of curves via Legendre-Gauss quadrature
[x] Intersects curves and computes cubic curve self-intersection to any degree of accuracy
[x] Determines bounding boxes, extrema,
[x] Locates nearest on-curve location to point
[x] to any degree of accuracy
[x] Splits curves into subcurves
[x] Offsets and outlines curves
[ ] Comprehensive Unit and Integration Test Coverage
[ ] Complete Documentation

Installation

CocoaPods

CocoaPods is a dependency manager for Cocoa projects. You can install it with the following command:

$ gem install cocoapods

To integrate BezierKit into your Xcode project using CocoaPods, add it to your target in your Podfile:

target '<Your Target Name>' do
    pod 'BezierKit', '>= 0.16.1'
end

Then, run the following command:

$ pod install

Swift Package Manager

The Swift Package Manager is a tool for automating the distribution of Swift code and is integrated into the swift compiler. Once you have your Swift package set up, adding BezierKit as a dependency is as easy as adding it to the dependencies value of your Package.swift.

// swift-tools-version:5.0
import PackageDescription

let package = Package(
    name: "<Your Target Name>",
    dependencies: [
        .package(url: "https://github.com/hfutrell/BezierKit.git", from: "0.16.1"),
    ]
)

Usage

Constructing & Drawing Curves

BezierKit supports cubic Bezier curves (CubicCurve) and quadratic Bezier curves (QuadraticCurve) as well as line segments (LineSegment) each of which adopts the BezierCurve protocol that encompasses most API functionality.

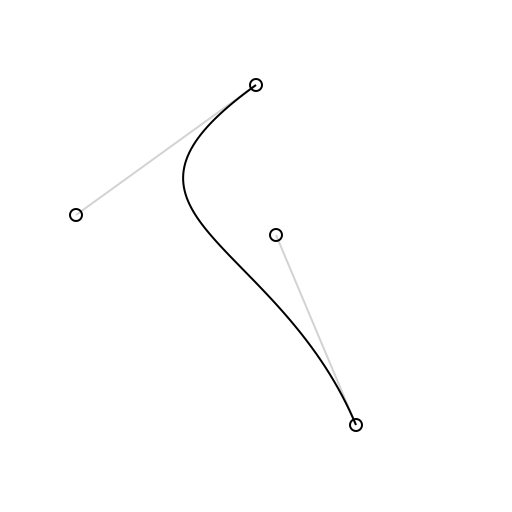
import BezierKit

let curve = CubicCurve(
    p0: CGPoint(x: 100, y: 25),
    p1: CGPoint(x: 10, y: 90),
    p2: CGPoint(x: 110, y: 100),
    p3: CGPoint(x: 150, y: 195)
 )

 let context: CGContext = ...       // your graphics context here
 Draw.drawSkeleton(context, curve)  // draws visual representation of curve control points
 Draw.drawCurve(context, curve)     // draws the curve itself

Intersecting Curves

The intersections(with curve: BezierCurve) -> [Intersection] method determines each intersection between self and curve as an array of Intersection objects. Each intersection has two fields: t1 represents the t-value for self at the intersection while t2 represents the t-value for curve at the intersection. You can use the point(at:) method on either of the curves to calculate the coordinates of the intersection by passing in the corresponding t-value for the curve.

Cubic curves may self-intersect which can be determined by calling the selfIntersections() method.

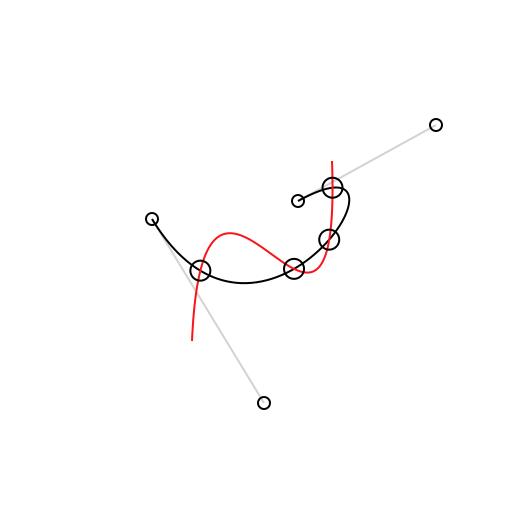
let intersections: [Intersection] = curve1.intersections(with: curve2)
let points: [CGPoint] = intersections.map { curve1.point(at: $0.t1) }

Draw.drawCurve(context, curve: curve1)
Draw.drawCurve(context, curve: curve2)
for p in points {
    Draw.drawPoint(context, origin: p)
}

Splitting Curves

The split(from:, to:) method produces a subcurve over a given range of t-values. The split(at:) method can be used to produce a left subcurve and right subcurve created by splitting across a single t-value.

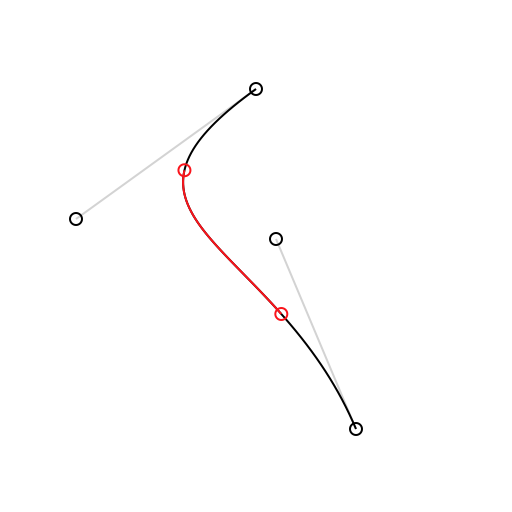
Draw.setColor(context, color: Draw.lightGrey)
Draw.drawSkeleton(context, curve: curve)
Draw.drawCurve(context, curve: curve)
let subcurve = curve.split(from: 0.25, to: 0.75) // or try (leftCurve, rightCurve) = curve.split(at:)
Draw.setColor(context, color: Draw.red)
Draw.drawCurve(context, curve: subcurve)
Draw.drawCircle(context, center: curve.point(at: 0.25), radius: 3)
Draw.drawCircle(context, center: curve.point(at: 0.75), radius: 3)

Determining Bounding Boxes

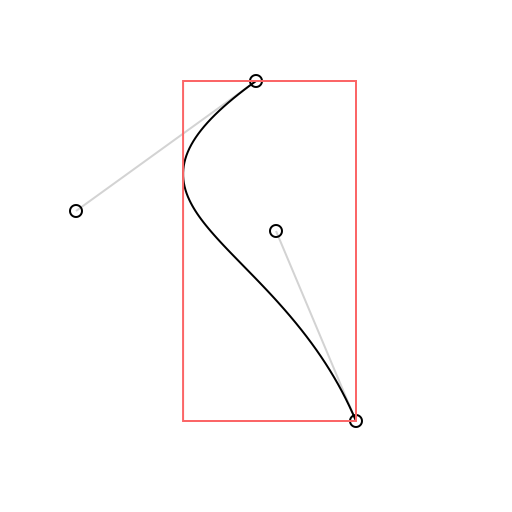
let boundingBox = curve.boundingBox
Draw.drawSkeleton(context, curve: curve)
Draw.drawCurve(context, curve: curve)
Draw.setColor(context, color: Draw.pinkish)
Draw.drawBoundingBox(context, boundingBox: curve.boundingBox)

BezierKit is a powerful library with a lot of functionality. For the time being the best way to see what it offers is to build the MacDemos target and check out each of the provided demos.

License

BezierKit is released under the MIT license. See LICENSE for details.

hfutrell / BezierKit

readme