mwa: Causal Inference in Spatiotemporal Event Data
mwa is a flexible methodological framework designed to analyze causal relationships in spatially and temporally referenced data. The study of political violence, in particular, has benefited in recent years from a rapid increase in the availability of such data sets. While progress has been made in relating conflict intensity to geographic conditions, more complex endogenous mechanisms that drive conflict at the micro-level remain largely elusive to quantitative analysis. To fill this gap, we introduce a novel approach to causal inference in disaggregated event data that combines two techniques for ensuring robust and clean causal inference: sliding spatiotemporal windows and statistical matching.
Specific types of events might affect subsequent levels of other events. To estimate the corresponding effect, treatment, control, and dependent events are selected from the empirical sample. Treatment effects are established through automated matching and a diff-in-diffs regression design. The analysis is repeated for various spatial and temporal offsets from the treatment events to address concerns related to the "modifiable areal unit problem" (MAUP). Instead of arriving at a single estimate for an arbitrary choice of spatiotemporal unit, results for many different such specifications are reported making the dependency on these choices explicit.
We here illustrate the methodology using an example from quantitative research on conflict but it could be equally applied in other quantitative fields of research that rely on geo-referenced event data: Criminologists might investigate the effects of law enforcement activities on subsequent levels of crime. Epidemiologists could analyze the spread of infectious disease as a function of specific types of interactions between individuals.
For further details on the methodological framework, please refer to the article of Schutte & Donnay that has appeared in Political Geography in 2014.
Installation
The package can be installed through the CRAN repository.
install.packages("mwa")Or the development version from Github
# install.packages("devtools")
devtools::install_github("kdonnay/mwa")Important: The size of the Java heap space has to be set before first calling the package via library(mwa) since JVM size cannot change once it has been initialized. This also implies that R has to be restarted if another library was already using a JVM in order for the heap space option to have any effect. To set the heap space to 1 GB, for example, use options(java.parameters = "-Xmx1g") (512 MB is the default size).
Usage
The following simple illustrations use simulated event data that are included with the package. Spatiotemporal patterns of "dependent", "treatment" and "control" type events are constructed to represent a specific causal effect of treatment versus control on the level of dependent events. All of our simulation tests use the smallest possible increment of 1 additional dependent event per treatment episode and no increase for control episodes. We specifically chose effect size 1 for two reasons. First, to pose a difficult simulation test for the method to pass. The larger the effect size, the easier it would be to recover the pattern. Second, to emulate the kind of effect sizes we see in empirical data. In fact, empirical effect sizes are often smaller than 1, i.e. on average we see a significant increase or decrease of effect size 1 in the dependent variable only after multiple "trigger" events.
data(mwa_data)The method expects data to be a data.frame. Dates must be given in column timestamp and formatted as a date string with format "YYYY-MM-DD hh:mm:ss". Data must also contain two entries called lat and lon for the geo-location of each entry.
Sliding spatio-temporal windows
The function matchedwake performs the Matched Wake Analysis (mwa), which consists of two steps: counts for previous and posterior events are established for different spatial and temporal windows. This approach is supposed for the MAUP problem explained above. Making the researcher decide which exact window sizes are appropriate is difficult due to the lack of theoretical expectations.
Why should events at a distance of 20 km be counted while events at a distance of 30 km be excluded?
The entire procedure of counting previous and subsequent events for every intervention is repeated for multiple sizes of spatiotemporal cylinders. This helps us to overcome the problem of inference hinging on arbitrary cell sizes and to distinguish among small- and large-scale effects empirically. For example, the effect of a treatment event on the level of dependent events might be stronger in its direct spatial and temporal vicinity and not affect more distant locations.
Statistical matching
After specifying the window sizes, the function carries out statistical matching on covariates. The general idea behind matching is to approximate as closely as possible experimental conditions in observational data. In experimental settings, treatment is applied randomly and its effects are observed in comparison to an untreated control group. The goal of matching is to increase balance, i.e. to make the empirical distributions of the covariates in the treatment and control group more similar. Matching has to be performed repeatedly for all spatial and temporal parameter combinations which is why we implement an automated matching technique called Coarsened Exact Matching (CEM). In CEM, substantially identical but numerically slightly different values are collapsed into bins of variable sizes for each covariate. Matching is then performed for observations belonging to the same bins. CEM generates well-balanced data sets by choosing bin sizes for different variables based on their empirical distributions.
Difference-in-differences regression
The treatment effect is estimated in a difference-in-differences regression design. To assess the within-subject before and after change, difference-in-differences performs an OLS regression on the matched data set to estimate changes in the number of dependent events brought about by the treatment. $n{post} = \beta{0} + \beta{1}n{pre} + \beta{2}treatment + u$ The dependent variable in this model is the number of dependent events after interventions. $\beta{1}$ estimates the impact of the number of dependent events before the intervention. $\beta_{2}$ is the estimated average treatment effect of the treated, i.e. the quantity of our interest.
Potential pitfalls
Spatiotemporal cylinders around interventions can overlap partially. If they do, the Stable Unit Treatment Value Assumption (SUTVA) inherent to matching is violated. It states that the treatment effect of any observation should be independent of the assignment of treatment to other units. Violating this assumption can lead to biased estimates. Two MWA scenarios are imaginable in which the SUTVA assumption would be clearly violated. First, multiple treatment events could overlap in space and time. Assuming a positive treatment effect, the corresponding estimates are likely to be biased upward in this scenario. Second, treatment and control events could overlap and thereby water down the treatment effect. In this case, the estimate for the treatment effect would be biased downward. Remember that the effect size in our simulated data is only 1. Thus for overlapping spatiotemporal episodes, where counts in the dependent category additionally vary due to the overlap, significant differences of 1 in the level of dependent events are increasingly difficult to detect.
The simplest way to avoid drawing false inference is therefore to check the data for overlaps of treatment and control events and select subsets that are not affected by this problem. For example, a civil war might go through phases of intense violence (e.g. summer offensives) and calmer periods, and researchers could test the causal effects of different types of events in the calmer periods to avoid false inference from overlapping events. However, empirical insights into the conflict dynamics would then, of course, be exclusively limited to such calmer periods instead of the entire conflict.
If substantial numbers of overlapping cylinders cannot be avoided, data can still be analyzed using MWA. In this situation, the following problem has to be accounted for: Interventions of different types prior to the intervention under investigation can affect subsequent levels of dependent events. As a result, the causal effect attributed to the intervention would be in fact the product of a specific mix of different interventions (a double treatment, for example). A simple remedy in this situation is to match on the numbers of previous treatment and control events. This ensures that the interventions retained in the post-matching sample have similar histories of treatment and control events. A third strategy is to simply remove overlapping observations from the sample. The obvious problem with this approach is the potential bias arising from non-random deletion itself.
Detailed statistics on the degree of overlaps are shown below with simulated data.
Specify model parameters
To call the matchedwake function we first need to specify all required parameters:
- t_window: specifies the minimal and maximal temporal window sizes and corresponding steps used in the iteration. Required syntax is c(min_window, max_window, step_size).
# - 2 to 10 days in steps of 2
t_window <- c(2,10,2)- spat_window: The spatial window spat_window is specified in the same way with kilometers as units.
# - 2 to 10 kilometers in steps of 2
spat_window <- c(2,10,2)- treatment, control, dependent: They define which category of events is considered to be treatment, control and dependent cases respectively. The required syntax is c(column_name, value) where column_name must be entered as String and value can be Numeric, Boolean, or a String.
# - column and entries that indicate treatment events
treatment <- c("type","treatment")
# - column and entries that indicate control events
control <- c("type","control")
# - column and entries that indicate dependent events
dependent <- c("type","dependent")- matchColumns: selects the columns in data used for matching. Matching variables are expected to be coded together with every treatment and control type event and are assumed to reflect a set of suitable matching variables (what is suitable will, of course, vary from case to case).
# - columns to match on
matchColumns <- c("match1","match2")Here we specify some optional parameters:
- regression type:
with the parameter
estimationyou can choose an estimation method: "lm" (linear model), "att" (estimation procedure from thecempackage) or "nb" (count dependent model). For regressions using "lm" or "att" we can weight the regression by the number of treatment vs. control cases. Additional control variables can be specified via estimationControls. For example, ifestimationControls = c("covariate1"), the package automatically modifies the estimation formula. In the output it returns the coefficients and p values for the treatment and all additional control variables.
estimation = "lm"
# - use weighted regression (default estimation method is "lm")
weighted <- TRUE
#include covariates
#estimationControls = c("covariate1")- temporal units: The optional argument t_unit specifies the temporal resolution for which the analysis is to be conducted, one of either "days", "hours", "mins" or "secs".
t_unit <- "days"- TCM: Boolean to select whether the method should match on counts of previous treatment and control instances
TCM <- TRUE- alpha: Significance levels can be specified to decide when a treatment effect is statistically significant where alpha1 is the first significance level used for the analysis and plots (Default = 0.05) and alpha2 is the second significance level used for the analysis and plots (Default = 0.1).
alpha1 <- 0.05
alpha2 <- 0.1 The package supports full inheritance for optional arguments of the following methods: cem and att (cem), lm (stats), glm.nb (MASS). The method name needs the prefix "packagename.method". For example, in order for cem to return an exactly balanced dataset simply add cem.k2k = TRUE.
Output
The matchedwake function returns an objects of class "matchedwake", which is a list of several objects. The standard print, summary and plot functions are overloaded to provide specific outputs for this class. We explain the output format in detail below illustrating how the results can be interpreted.
#call matchedwake function
results <- matchedwake(mwa_data, t_window, spat_window, treatment, control, dependent, matchColumns, weighted = weighted, t_unit = t_unit, TCM = TCM)## MWA: Analyzing causal effects in spatiotemporal event data.
##
## Please always cite:
## Schutte, S., Donnay, K. (2014). "Matched wake analysis: Finding causal relationships in spatiotemporal event data." Political Geography 41:1-10.
##
##
## ATTENTION: Depending on the size of the dataset and the number of spatial and temporal windows, iterations can take some time!
##
## matchedwake(data = mwa_data, t_window = t_window, spat_window = spat_window, ...):
## Using JVM with 0.4 GB heap space...
## [OK]
## Matching observations and estimating causal effect........................[OK]
## Analysis complete!
##
## Use summary() for an overview and plot() to illustrate the results graphically.In estimates we find an overview over the diff-in-diff results. The treatment effect is estimated for every combination of spatial and time window sizes in the range that we specified above. The column estimate gives the corresponding coefficient for the treament dummy. Columns pvalue and adj.r.squared gives diagnostics if an estimate was statistically significant and how much of the variance of the dependent variable we can explain respectively. If
additional control dimensions were included in the estimation, it further returns the corresponding coefficients and p values.
results$estimates## t_window spat_window estimate pvalue adj.r.squared
## 1 2 2 0.00000000 1.000000e+00 0.00000000
## 2 2 4 0.00000000 1.000000e+00 0.00000000
## 3 2 6 0.00000000 1.000000e+00 0.00000000
## 4 2 8 0.00000000 1.000000e+00 0.00000000
## 5 2 10 0.00000000 1.000000e+00 0.00000000
## 6 4 2 0.00000000 1.000000e+00 0.00000000
## 7 4 4 0.00000000 1.000000e+00 0.00000000
## 8 4 6 0.07692308 2.272969e-01 -0.01260684
## 9 4 8 0.00000000 1.000000e+00 0.00000000
## 10 4 10 0.00000000 1.000000e+00 0.00000000
## 11 6 2 0.00000000 1.000000e+00 0.00000000
## 12 6 4 0.00000000 1.000000e+00 0.00000000
## 13 6 6 0.04166667 6.415146e-01 -0.05500615
## 14 6 8 0.00000000 1.000000e+00 0.00000000
## 15 6 10 0.00000000 1.000000e+00 0.00000000
## 16 8 2 0.00000000 1.000000e+00 0.00000000
## 17 8 4 0.00000000 1.000000e+00 0.00000000
## 18 8 6 0.00000000 1.000000e+00 0.00000000
## 19 8 8 1.00000000 1.771583e-05 0.83958974
## 20 8 10 0.88888889 3.117263e-04 0.70933769
## 21 10 2 0.00000000 1.000000e+00 0.00000000
## 22 10 4 0.00000000 1.000000e+00 NaN
## 23 10 6 0.00000000 1.000000e+00 0.00000000
## 24 10 8 1.00000000 1.110157e-04 0.79289941
## 25 10 10 1.00000000 2.913782e-04 0.74297308matching gives a data.frame with detailed matching statistics for all spatial and temporal windows considered. Returns the number of control and treatment episodes, L1 metric, percent common support. All values are given both pre and post matching. L1 is a multivariate distance metric expressing the dissimilarity between the joint distributions of the covariates in treatment and control groups. To calculate this statistic, the joint distributions are approximated in fine-grained histograms. Average normalized differences between these histograms are expressed in the L1 statistic ranging from complete dissimilarity Common support expresses the overlap between the distributions of matching variables for treatment and groups in percent. 100% common support refers to a situation where the exact same value ranges can be found for all matching variables in both groups.
results$matching## t_window spat_window control_pre treatment_pre L1_pre commonSupport_pre
## 1 2 2 50 25 0.44 47.6
## 2 2 4 50 25 0.44 45.5
## 3 2 6 50 25 0.44 41.7
## 4 2 8 50 25 0.46 38.5
## 5 2 10 50 25 0.50 35.7
## 6 4 2 50 25 0.46 43.5
## 7 4 4 50 25 0.52 38.5
## 8 4 6 50 25 0.58 30.0
## 9 4 8 50 25 0.60 29.0
## 10 4 10 50 25 0.64 24.2
## 11 6 2 50 25 0.46 43.5
## 12 6 4 50 25 0.54 37.0
## 13 6 6 50 25 0.62 29.0
## 14 6 8 50 25 0.64 27.3
## 15 6 10 50 25 0.72 19.4
## 16 8 2 50 25 0.46 43.5
## 17 8 4 50 25 0.54 37.0
## 18 8 6 50 25 0.62 29.0
## 19 8 8 50 25 0.68 20.9
## 20 8 10 50 25 0.74 17.0
## 21 10 2 50 25 0.46 43.5
## 22 10 4 50 25 0.54 37.0
## 23 10 6 50 25 0.62 29.0
## 24 10 8 50 25 0.66 20.5
## 25 10 10 50 25 0.72 15.2
## control_post treatment_post L1_post commonSupport_post
## 1 22 14 0.448 53.3
## 2 22 14 0.448 53.3
## 3 21 14 0.429 53.3
## 4 21 14 0.429 53.3
## 5 20 13 0.373 70.0
## 6 22 14 0.448 53.3
## 7 21 12 0.393 70.0
## 8 20 13 0.423 50.0
## 9 19 12 0.390 60.0
## 10 18 12 0.361 66.7
## 11 22 14 0.448 53.3
## 12 20 12 0.417 60.0
## 13 20 12 0.433 50.0
## 14 19 11 0.397 60.0
## 15 14 10 0.329 62.5
## 16 22 14 0.448 53.3
## 17 20 12 0.417 60.0
## 18 19 11 0.397 60.0
## 19 9 9 0.333 44.4
## 20 10 9 0.267 55.6
## 21 22 14 0.448 53.3
## 22 20 13 0.473 46.7
## 23 18 11 0.409 60.0
## 24 8 8 0.375 37.5
## 25 8 7 0.321 42.9SUTVA yields a data.frame with detailed statistics on the degree of overlaps of the spatiotemporal cylinders. Returns the fraction of cases in which two or more treatment (or control) episodes overlap (SO: same overlap) and the fraction of overlapping treatment and control episodes (MO: mixed overlap). All values are given pre and post matching and for the full time window.
results$SUTVA## t_window spat_window SO_pre SO_post SO MO_pre MO_post MO
## 1 2 2 0.000 0.000 0.000 0.000 0.000 0.000
## 2 2 4 0.013 0.000 0.013 0.000 0.000 0.000
## 3 2 6 0.013 0.000 0.013 0.000 0.000 0.000
## 4 2 8 0.027 0.013 0.040 0.000 0.000 0.000
## 5 2 10 0.027 0.013 0.040 0.000 0.000 0.000
## 6 4 2 0.013 0.013 0.027 0.000 0.000 0.000
## 7 4 4 0.027 0.013 0.040 0.013 0.013 0.027
## 8 4 6 0.027 0.013 0.040 0.013 0.013 0.027
## 9 4 8 0.040 0.027 0.067 0.027 0.027 0.053
## 10 4 10 0.040 0.027 0.067 0.027 0.027 0.053
## 11 6 2 0.013 0.013 0.027 0.000 0.000 0.000
## 12 6 4 0.040 0.027 0.067 0.013 0.013 0.027
## 13 6 6 0.040 0.027 0.067 0.013 0.013 0.027
## 14 6 8 0.053 0.040 0.093 0.027 0.040 0.067
## 15 6 10 0.053 0.040 0.093 0.027 0.040 0.067
## 16 8 2 0.013 0.013 0.027 0.000 0.000 0.000
## 17 8 4 0.040 0.027 0.067 0.013 0.013 0.027
## 18 8 6 0.040 0.027 0.067 0.013 0.013 0.027
## 19 8 8 0.067 0.053 0.107 0.040 0.053 0.093
## 20 8 10 0.067 0.053 0.107 0.040 0.053 0.093
## 21 10 2 0.013 0.013 0.027 0.000 0.000 0.000
## 22 10 4 0.040 0.027 0.067 0.013 0.013 0.027
## 23 10 6 0.053 0.040 0.093 0.013 0.013 0.027
## 24 10 8 0.067 0.053 0.107 0.040 0.053 0.093
## 25 10 10 0.107 0.093 0.187 0.040 0.053 0.093wakes provides a data.frame with the information for the spatiotemporal cylinders (or wakes) for all spatial and temporal windows considered. Returns the eventID (i.e., the index of the event in the time-ordered dataset), treatment (1: treatment episode, 0: control episode), counts of dependent events, overlaps (SO and MO) pre and post intervention, and the matching variables.
head(results$wakes,20)## eventID t_window spat_window treatment dependent_pre dependent_trend
## 1 19 2 2 0 0 0
## 2 22 2 2 0 0 0
## 3 37 2 2 1 0 0
## 4 38 2 2 0 0 0
## 5 42 2 2 0 0 0
## 6 43 2 2 0 0 0
## 7 44 2 2 0 0 0
## 8 45 2 2 0 0 0
## 9 47 2 2 1 0 0
## 10 48 2 2 1 0 0
## 11 51 2 2 1 0 0
## 12 65 2 2 0 0 0
## 13 71 2 2 0 0 0
## 14 72 2 2 0 0 0
## 15 77 2 2 1 0 0
## 16 81 2 2 0 0 0
## 17 94 2 2 0 0 0
## 18 96 2 2 0 1 1
## 19 100 2 2 0 0 0
## 20 101 2 2 0 0 0
## SO_pre MO_pre dependent_post SO_post MO_post match1 match2
## 1 0 0 0 0 0 0.8723574 1.0078108
## 2 0 0 0 0 0 1.0157923 1.0096824
## 3 0 0 0 0 0 0.9076430 1.0129783
## 4 0 0 0 0 0 1.0136693 1.0059419
## 5 0 0 0 0 0 0.8102220 0.9803980
## 6 0 0 0 0 0 0.8668484 1.0091446
## 7 0 0 0 0 0 1.0055768 0.9937506
## 8 0 0 0 0 0 0.9510178 0.9869921
## 9 0 0 0 0 0 1.0461257 0.9850034
## 10 0 0 0 0 0 0.8090028 0.9874669
## 11 0 0 0 0 0 1.1104018 1.0024844
## 12 0 0 0 0 0 0.9656787 1.0040250
## 13 0 0 0 0 0 0.8099484 1.0134585
## 14 0 0 0 0 0 0.9113120 1.0097070
## 15 0 0 0 0 0 1.0153000 0.9954609
## 16 0 0 0 0 0 1.1694675 1.0072423
## 17 0 0 0 0 0 0.9392289 0.9863395
## 18 0 0 0 0 0 1.0963351 0.9986607
## 19 0 0 0 0 0 1.1004724 1.0090538
## 20 0 0 0 0 0 0.9958809 0.9932350The summary() function returns a data.frame with an overview of all significant results (significance level is alpha1). If detailed = TRUE this overview includes a number of matching statistics and statistics on overlaps of the spatiotemporal cylinders. If additional control dimensions were included in the estimation, it also provides an overview of the corresponding coefficients and p values for all significant results.
# Return detailed summary of results:
summary(results, detailed = TRUE)## Results:
## The method has identified combinations of temporal and spatial window sizes with significant estimates. The table below gives the estimated effect sizes and p-values for these combinations as well as summary post-matching statistics and statistics on SUTVA violations:
## Matching:
## - '%treat' is short for the percentage of treatment events; the closer this is to 50%, the better the balance of treatment and control cases after matching
## - 'L1metric' measures the covariate balance after matching
## - '%supp' is short for percentage of common support after matching, a standard measure for the overlap of the range of covariate values
## SUTVA violations:
## - '%SO' gives the percentage of cases in which two or more treatment (or control) episodes overlap
## - '%MO' provides the fraction of overlapping treatment and control episodes## Time[days] Space[km] EffectSize p.value adj.Rsquared %treat L1metric
## 1 8 8 1.000 0 0.8396 50.0 0.333
## 2 8 10 0.889 0 0.7093 47.4 0.267
## 3 10 8 1.000 0 0.7929 50.0 0.375
## 4 10 10 1.000 0 0.7430 46.7 0.321
## %supp %S0 %MO
## 1 44.4 10.7 9.3
## 2 55.6 10.7 9.3
## 3 37.5 10.7 9.3
## 4 42.9 18.7 9.3Visualization
plot() returns a contour plot: The lighter the color the larger the estimated treatment effect. The corresponding standard errors are indicated by shading out some of the estimates: No shading corresponds to p < alpha1 for the treatment effect in the diff-in-diffs analysis. Dotted lines indicate p-values between alpha1 and alpha2 and full lines indicate p > alpha2. The cells indicating effect size and significance level are arranged in a table where each field corresponds to one specific combination of spatial and temporal sizes.
# Plot results:
plot(results)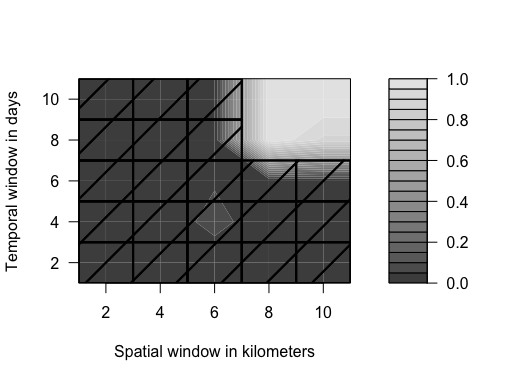
Meta
- Please report any issues or bugs.
- License: LGPL-3
- Get citation information for
mwain R usingcitation(package = 'mwa') - CRAN: https://cran.r-project.org/package=mwa
- Check out our article in Political Geography for more details on the methodology and its applications to conflict research.