search

kiwi0fruit / ultimate-question

Open-ended natural selection of interacting code-data-dual algorithms as a property analogous to Turing completeness.
https://www.reddit.com/r/compsci/comments/97s8dl/on_natural_selection_of_the_laws_of_nature/
Other
12 stars 0 forks source link
artificial-life ethics evolution meta-ethics metaethics natural-selection open-ended-evolution open-endedness theory-of-computation theory-of-everything turing-completeness universal-darwinism

readme

DOWNLOAD ZIP BACKUP: ultimate-question.zip

_UPDATE WARNING: This article is somewhat outdated. It is advised to start reading from On Natural selection of the laws of nature, Artificial life, Open-ended evolution of Interacting code-data-dual algorithms, Universal Darwinism and Buddhism-like illusion of the Self article._

The Ultimate Question of Life, the Universe, and Everything

aka The simplest artificial life model with open-ended evolution as a possible model of the universe, Natural selection of the laws of nature, Universal Darwinism, Occam's razor

Peter Zagubisalo, January 2016, minor update July 2018

NEW UPDATES

Introduction contents

Intro pt.1

≡←

_UPDATE WARNING: This article is somewhat outdated. It is advised to start reading from On Natural selection of the laws of nature, Artificial life, Open-ended evolution of Interacting code-data-dual algorithms, Universal Darwinism and Buddhism-like illusion of the Self article._

Greetings,

I seek advice or any other help available regarding creating a specific mathematical model. It’s origin is at the intersection of the following areas:

The problem I’m trying to solve can be described as to create the simplest artificial life model possible with open-ended evolution (open-endedness means that the evolution doesn't stop on some level of complexity but can progress further to the intelligent agents after some great time). There are analogues to laws of nature in this dynamic model: 1) postulates of natural selection + some unknown ontological basis, 2) pool of phenotypes of evolving populations that are relatively stable on some time periods so they can be considered "laws". This approach implies indeterminism and postulates random and spontaneous nature of some events. It is also assumed that the universe had the first moment of existence with relatively simple structure.

Intro pt.2: Key ideas

≡←

The key idea of this research program is to create an artificial universe in which we can answer any questions like "why is the present is this way not another?", "because of what?" (it's a better formulated ancient question "Why is there something rather than nothing?"). So any existing structures can be explained: as much entities as possible should have a history how they appeared/emerged - instead of postulating them directly. Moreover the model itself needs to have some justification (to be a candidate for model of the our real universe).

There are two main intuitions-constraints for this universe: 1) the start from the simple enough state (the beginning of time), 2) the complexity capable of producing sentient beings (after enormous simulation time of course) comes from natural selection which postulates are provided by universe model rules. The two intuitions give hope that the model to build would be simple and obvious in retrospect like postulates of natural selection are simple and obvious in retrospect (they are obvious, but until Darwin formulated them it was really hard to assume them). So there is a hope that it's feasible task.

The model to build is a model of complexity generation. At later steps the complexity should be capable of intelligence and self-knowledge. Sadly I have not moved far to this goal. I'm still in the situation of "I feel like the answer the this grand question can be obtained this particular way"

Intro pt.3: Justification and best tools

≡←

Those two intuitions come from the following:

The best tool I know that can historically explain why the particular structures exist is Darwin's evolution with natural selection. And the best tools to justify the model of reality are falsifiability and Occam's razor. First states that the theory should work and be capable of predictions. The second states that among models similar in respect to falsifiability the simplest one should be chosen.

If we are to go with natural selection as novelty generating mechanism then we should think that Lee Smolin's Cosmological natural selection (CNS) hypothesis is likely to be true. And that means that our observable universe could have had a very large number of universes-ancestors. This means that it would be really hard to apply falsifiability to the model to build. In the best case when built (sic!) it could provide the basis for General relativity + Quantum mechanics unification theory (or could not...). In the worst case we only get the restriction that our universe is possible in the model. I.e the populations of individuals that resemble our laws of physics should be probable to appear and our particular laws of physics are definitely possible to appear (either it's a group dynamic or a single individual universe like in CNS).

Luckily we also have an artificial life open-ended evolution (a-life OEE) restriction and Occam's razor. OEE means that at least in itself the model must show specific dynamics. And we already can assume that the model should be as simple as possible (and if the assumed simplicity is not enough then we should make it more complex). Though simplicity by itself cannot be a justification I have a hope that selecting the simplest workings from many working a-life OEE models could be a justification (proof of the theorem that the selected workings should be in every a-life OEE would be even better). And I mean a justification for basic rules that govern the dynamic of the model. By the way, this way we can justify a model obtained via any other research program. So if some "Theory of everything" appears we don't need to ask "why this particular theory?". Instead we should check for other (simpler?) models that do their work as good and then reason of necessary and sufficient criteria.

More about justification: Are Universal Darwinism and Occam's razor enough to answer all Why? (Because of what?) questions?

Intro pt.4: The model

≡←

The research program uses the artificial life model with natural selection as a basis. This means taking inspiration in natural selection of biological life (NS). Also adding Occam's razor (OR) to the picture. In order to continue we need to precisely define what are individuals in the model (and environment if needed) and how the process of their replication and death takes place. There are some properties of the model we can assume and go with:

Intro pt.5: Obvious problems, incl. what is inanimate matter? what about quantum computers?

≡←

1. If we assume that complex laws are emergent from algorithms then what about quantum computers? question needs answering. It can be formulated as "Is bounded-error quantum polynomial time (BQP) class can be polynomially solved on machine with discrete ontology?"

What is your opinion and thoughts about possible ways to get an answer whether problems that are solvable on quantum computer within polynomial time (BQP) can be solved withing polynomial time on hypothetical machine that has discrete ontology? The latter means that it doesn't use continuous manifolds and such. It only uses discrete entities and maybe rational numbers as in discrete probability theory?

2. If we go with natural selection, use biological life as inspiration and go with assumptions above then we should answer the question: what is the inanimate matter?

For biological life the inanimate matter is only an environment. And if we have only individuals in the model then why the inanimate matter in our Universe is so stable? After all in the biological life there is always the threat of cancer that is an error in the reproduction algorithm. Why some elemental particles never ever "mutate"? (only expanding space puts some doubts to the picture but it doesn't seem to be related to the question). This requires explaining via model assumptions or correcting them.

Ideas about possible solutions:

Intro pt.6: P.S, discussion, subscribe, source code repository

≡←

You can discuss the letter on GitHub or Reddit.

This introduction actually contains everything important that is in this article. So the rest text at best can add some details to the picture or answer some questions. At worst it can be outdated and no longer reflects my opinion.

Appendix contents

≡←

0. Short formulation of the problem

≡↑

A. The model as the process of natural selection

The postulates of natural selection:

During natural selection the information about the environment “imprints” into the structure of individuals.

Presumably the environment will be other individuals, and there would be nothing but individuals. It may even be very primitive “atomic” individuals (whatever that means).

For natural selection to work, individual and its descendants must meet very similar events and interactions. “Reproduction” (p3) provides an environment of identical individuals. But apart from similar events they meet new and unique ones, which are provided by “variation” (p5).

B. The model as the structure that changes in time

It can be assumed that individuals are stable patterns like waves existing in the discrete structure. Their origin may even be the topological curvature (knots? braids?). The patterns should be resistant to perturbations. Presumably perturbations arise from reproduction and variation postulates of natural selection.

The process starts from a very simple state of the structure. It may be something like “nothing”, the empty set, “unity” or “one”. But the state of minimum complexity from which the process begins is still under consideration.

The rules or meta-rules of changing this simple state must be initially defined.

Presumably, the rules at the same time give rise to the structure that consist of interconnected atomic parts, and produce the natural selection of patterns in the structure.

The structure is discrete and finite. Steps of time that correspond to changes in the structure, are also discrete.

C. So the two views on the model to create:

  1. The model as the process of natural selection
  2. The model as the structure that changes in time.

The subproblem I’m trying to solve at the moment is the following:

1) How is it that the pattern in the structure is the same as the individual in the natural selection? So it’s necessary to combine two views on the process and create a complete and holistic picture. And the pattern and the individual are the same in that picture.

2) What are the “atoms” in this structure? What’s the basis of this picture? May be the atomic parts in the structure similar to a graph are the atomic individuals. And these atomic individuals easily increase their number. Then how do non-atomic individuals appear?

So my question is a request for intuitions on how to create that complete picture that satisfies the constraints.

0.1 The first two hardest problems I struggled and haven't solved

≡↑

The two hardest problems I struggled and haven't solved are about 1) how to define fixed laws that govern structure change (meta-laws?) and 2) what means the simplest model. And even more: that two problems seem to be two sides of the same single problem.

From simple point of view we should not really expect to get all laws of nature from our particular real universe if we are to discover laws via natural selection modelling. The laws of nature should be populations of individuals that share quite similar features (like “genes”). That populations slowly change in time but we are to expect them to change gradually and slowly so if we are to examine/investigate simulation of the desired mathematical model we can distinguish periods when population features are more or less stable. That populations also do not stop their evolution on some fixed level of complexity (see open-ended evolution) - they should be capable of producing complex “intelligent” agents after some presumably great time (to actually get intelligent agents in simulation is impossible with our limited resources/abilities).

But from the second point of view we should define laws of nature in a common way: the laws (meta-laws?) that govent natural selection and provide postulates of natural selection to the model. And this is where we get metaphysics involved with Occam's razor and the question of “What is the simplest?”. The guiding constraint of my research program is that the desired model should be the simplest to the point of being self-justifying. That's important because I only have metaphysics philosophy considerations for this. And philosophy considerations should be obvious (or close to it) to be useful. For example from philosophy point of view we can argue that the Universe should've had the simplest first state at the first moment of time (1: the World wasn't created this morning with me unshaven, 2: we do not hide behind infinite causal chain that goes back to the past like ancient Greek hide gravitation pull to the Earth behind infinite elephants that the great turtle rest on). Or that discrete countable infinite time and discrete finite space is preferable over uncountably infinite time and infinite space. And Occam's razor presumption is quite good for justifying it. That's good but drastically not enough to build a math model.

So we need to define these meta-laws that simple to the point of being self-justifying... It's still possible to go with for no reason particular laws that are not self-justifying but with this we lose the only way of pure philosophy justifying. And we also already do not have empirical justifying because if we are to go with natural selection thing then we should think that Lee Smolin's Cosmological natural selection hypothesis is likely to be true. And that means that our observable universe could have had a very large number of universes-ancestors. So our real universe would definitely be out of our modelling abilities even if we have the desired model formulated. So we have no choise but to define these meta-laws that simple to the point of being self-justifying.

I have an intuitive feeling that some intuitive concepts like causation, recursion, reproduction/doubling, randomness/spontaneous symmetry breaking, natural selection can be obvious and self-justifying to be at that simple first state but at the moment my thoughts about them is more like a mess than something useful. The part that saddens me most is the desire to get rid of meta-laws completely and to “incapsulate” them into the graph-like structure (whatever that means), to make them “immanent”...

But at the same time the self-justification mentioned is based on my own sense of what should be done (aesthetics of a brain - trained neural network). And it might be not enough to properly define and justify the initial hardcoded meta-laws that provide medium for natural selection to work on. I believe some of that aesthetics are good to go and should not be revised as they are enough self-justified: like discrete time and space, the first "simplest" state at the first moment of time, incorporation of natural selection postulates in some way. But what means “simplest” and details how to include natural selection are not-yet-defined so it's the target of research.

Rest of my aesthetics try to guide me how to add that. But problems arise... Actually there might be another way: to solve “open-ended evolution” problem (OEE) by chance or blind variation (or any other way). Then try to strip as much from the model as possible and see if it's can be viewed as self-justifying from philosophical point of view. But it's a risky way as it may be that we would not be able to strip enough to justify. But considering the complexity of the OEE problem itself stripping still can be possible as OEE problem is not solved and still lack some important “puzzle piece”. But it may also be that my aesthetics of minimality of the model can actually help to build a model of OEE.

This whole task mostly is in the metaphysics and mathematics intersection. The one to accomplish it should be serious about both 1) precise math definitions and processes descriptiopns and 2) metaphysics problems and reasoning. If one to ignore, belittle or downplay either of two components then he is unlikely to succeed in this particular direction.

1. The physical and philosophical background of this problem

≡↑

   The general idea of the research program can be summarized as follows: to describe the beginning of the universe (and its development during first time) using the language of the theory of evolution. It’s assumed that the universe had the simple starting structure (the beginning). And the task is to describe mathematically accurate the starting structure and the process of it’s development in time. It also might be that there exist convincing arguments in favor the impossibility of creating that mathematical model.

1.1 Reminding the foundations of the theory of evolution

≡↑

   To begin with, I will briefly remind the foundations of the theory of evolution. This theory is the cornerstone of the research program.

   Darwin’s theory of evolution is a theory that describes the process in which relatively simple structures transform into more complex structures under the influence of simple factors. The simple factors are the postulates of the natural selection:

As noted by Karl Popper the theory of evolution is a theory of gradual changes that does not permit spontaneous appearance of monsters such as Boltzmann brain. This theory explains the entire path traversed by the life from the first unicellular organisms to Homo sapiens. And they differ much in complexity.

   The only one known to me explanation of how the complexity emerges from the simplicity is the theory of evolution. The complexity emerges by itself (!) and gradually when conditions (p1)-(p5) are met.

1.2 The description of the research program

≡↑

   As already mentioned, the general idea of the research program can be summarized as follows: to describe the beginning of the universe (and its development during first time) using the language of the theory of evolution. It’s assumed that the universe had the simple starting structure (the beginning). And the task is to describe mathematically accurate the starting structure and the process of it’s development in time.

This problem is put under the following assumptions:

(a) The universe is entirely knowable by humans. The birth of the universe is also knowable. It is a kind of epistemological optimism. But at the same time, this knowledge and understanding may be unfalsifiable. The history is full of facts that can be assumed, but can not be verified (fortunately, not all the facts are such). The hypotheses about the past have this remarkable feature.

(b) The universe is finite at every moment of time. The present was preceded by a finite number of moments of time. The assumption of finiteness is akin to intuitionistic revision of mathematics. It’s a doubt that it’s correct to use the actual infinity. It is something like Ockham’s razor: do not assume infinity until the possibility of creating a theory of a finite universe had been investigated. Since we assume the absence of actual infinity, there remains a choice between an infinite number of moments of time in the past and finite number. A finite amount is less complex, so the priority is to investigate this possibility. As a result, the potential infinity (but not the actual infinity) remains only in the process of appearance of the future moments of time.

(c​) There is a hypothesis that using the principles of the theory of evolution we can explain the origins of everything that precedes unicellular life. At least we can explain the origins of life (abiogenesis). But it’s not the most interesting thing. The most interesting thing is to explain the origin of inanimate matter. Given the fact that the theory of evolution explains the emergence of more complex structures from less complex structures, it can be expected that the earlier back in time we “return” the more simple structures we get. It could be more simple structures in terms of yet unknown statistical description. It is still the subject of discussion. So then the question arises: how simple the structure would be at the very beginning? “Nothing”, the empty set, “unity”, “one” or concepts of comparable simplicity come to mind. It also may be a more complex structure. A simple structure but not simpler than necessary. So the development of the universe from a very primitive state driven by evolution can be assumed. This implies spontaneous events of structure changes. And with these events the structure becomes more and more complex. The postulation of spontaneous events is what occurs in (p5) “variation”. There are also intuitions that postulate (p3) “reproduction” is also very important in this picture (This postulate describes at least a doubling of the existing structures). Spontaneous symmetry breaking may also be relevant.

   Paragraph (c​) is an intuitive guess. It echoes the ideas of Charles Peirce: his ideas of tychism and evolution of the laws of nature. In paragraph (c​) the laws of nature are like encapsulated in the evolving structures. Perhaps the laws can be derived from the structures with the help of statistical description. This, in turn, echoes the ideas of Ilya Prigogine and his attempts to get the arrow of time and irreversibility from the statistical description of ensembles in classical mechanics and his special version of quantum mechanics. There are also his ideas of synergetics and the birth of order from chaos.

(d) Thus, the initial idea was to create a mathematical model that incorporates the following principles:

And then to see if in this model would be stable structures (patterns?) that reproduce themselves and change over time. On the other hand modern theories that describe the fundamental workings of the universe, take into account the reality as it is now. That theories make the reconstruction of the past taking into account the reality as it is now. If we are under the assumptions (a), (b), (c​), then that theories must take into account the complexity that has arisen since the birth of the universe. We can only speculate about the age of the universe before the Big Bang. For example, according to the hypothesis of cosmological natural selection [1] our observable universe could have had a very large number of universes-ancestors. So the total age of the entire universe could be enormous. The research program I have described in this letter is an attempt to cheat and do not take into account the full history and complexity that may be enormous. It’s like a research “landing operation” in the past, an attempt to describe the universe from the very beginning of it, when it had a much simpler structure. Of course, this “landing” suffers from the lack of experimental evidence and verifiability. But the first goal is a proof of the concept: to create a model of primitive structures that survive (exist) and evolve over time. It is worth mentioning that the time should be real and fundamental in this evolutionary approach which is consistent with the ideas of Lee Smolin [2]. Perhaps in case of a successful first step, the ways of linking this approach with the observable universe may be found. If not then the methods of this approach (that are yet to be found) may be brought to other areas of scientific research. Which is also good.

(e) The presumption of the existence of the objective reality (objectivity) plays an important role in attempts to construct a mathematical model that satisfies the insights mentioned above. Objective reality can be conceived independently of the perception of observers. In mathematical physics, the objective reality is determined by specifying equivalence classes in the set of reality descriptions in terms of different observers (different coordinate systems, etc.). The dependent on the observer part of the description is not included in the equivalence class. This procedure is called “gauging away” [2].

The described research task is proposed to be accomplished by creating the mathematical model that is partly described in the section 2.

2. The main features and problems of/in the mathematical model to create

≡↑

The mathematical model is constructed in the framework of research task described in the section 1.

2.1 First overview of the mathematical model to create

≡↑

   Some properties possessed by the mathematical model can already be assumed. The model is mathematical in the sense that it is required to build a unified language of envisioning and thinking about a specific process in time. This process is still far from clear and whole picture. Here I am referring to mathematics as a unified language for describing and modeling the reality and possible reality.

   The mathematical model is intended to describe the process of changing of a particular structure (consisting of interconnected atomic parts). Moreover, it should be the process of development and complication of the structure.

   Regarding the nature of mathematical models: mathematics, mathematical models and constructs are created by people. Before the act of creation they do not exist. But the interesting thing is that the models can be isomorphic to the part of the reality.

2.2 The model as the process of natural selection

≡↑

   There is a short list of the postulates of natural selection (there is a more detailed list of the postulates in section 1):

   The process of natural selection can be viewed as the process of transferring information from the individual to it’s offspring. It is the information about possible interactions of the individual with the environment (and about reactions of the individual to these interactions). Among others this point of view is being promoted by Chris Adami [3]. Something like BVSR (“blind variation with selective retention” introduced by Donald T. Campbell [4]) can be mentioned as an example. If a specific structure of the individual promotes that the number of it’s offspring is larger than the number of competing individuals offspring then that specific structure will spread. Individuals that are less “fit” will die, and more “fit” individuals will multiply. So the information about the environment “imprints” into the structure of individuals.

2.3 The model as the structure that changes in time

≡↑

   Previously described point of view on the model partly shows mechanisms of it’s evolution and increasing complexity. There is also a point of view on the model as on the structure that changes in time. It is not clear what are the individuals in that structure. It can be assumed that individuals are stable patterns like waves existing in the discrete structure that consists of interconnected parts (like graph). Their origin may even be the topological curvature [5] (knots? [6] braids? [7, 8]). The patterns should be resistant to perturbations. The origin of these perturbations is not yet determined. Likely, it should take into account the postulates of the natural selection. The process of changing the structure in time can be similar to the following views:

2.4 The pattern in the structure is the same as the individual in the natural selection

≡↑

   At the moment I’m trying to find an answer to the following question: how is it that the pattern in the structure is the same as the individual in the natural selection?

   In other words it’s necessary to combine two previously outlined views on the process and create a complete and holistic picture. And the pattern and the individual are the same in that picture.

This inevitably requires answers to the following questions:

   The question is about creation of a mathematical dynamic model that satisfies the described conditions. At this point of research I lack intuitive insights on possible structures of that model. So the possible algorithm is to generate a guess on the structure and then check whether it fits conditions. It’s mostly a mathematical problem.

2.5 Other properties of the model: separability, meaning of life, strange loop, agents with free will, algorithms

≡↑

There are some other properties of the mathematical model to create that can be assumed. The following points are even more intuitive and far-fetched than the previously described. Actually this section is a short conspect of my chaotic ideas.

  1. On any steps of the process the “structure” is “separable” in a sense that it can be split into parts that we people can reason about and find the laws in. But there can be a hierarchy of such “separable” layers. I guess if the Universe didn't posses a feature like that it would not be knowable by humans. But still it is (to some big enough degree at least). So the “separability” is somehow connected with epistemological optimism (see above in the section 1.2a). I don't know of the cases where Reductionism doesn't work and hierarchy of knowable abstractions is not possible. This may mean that the natural selection rejects too topologically tangled systems (if we are under assumptions in the section 2.2). Or the entropy somehow related to this...

    • The idea-metaphor that I call “Cancer Langoliers” can be connected with entropy and difficulties for too topologically tangled systems. What if we look at the desired model as the structure that changes in time and imagine uncontrollably multiplying and reproducing individuals – and it's actually the basic level of the model. And the more complex structures to appear must survive in this chaotic permanently expanding mess. But the “mess” can also be non-permanently-expanding if we are to introduce some “reset” mechanism like mentioned in the next item in the list.

  2. The notion of “meaning of life” can be useful for creating the model. If we look at natural selection postulates the only candidates for the “meaning of life” are 1) the competition between evolutionary branches (survival of the particular evolutionary branch not the other branches), 2) survival and complication of the all branches hence the complication of awareness of individuals of the environment and themselves. The first point seem to be more likely but the second one is also worth consideration. And embracing 1) or 2) has different impact on the properties of the model to create. As described above, the model likely should get a hierarchy of “layers” (not the time layers) and the “higher” levels should be able to contain more complexity than the previous layers. If we are to assume 2) then the model should have (by design) the chance of reseting to the previous simple layer so that the “life” in the next more complex layer “died” (in this case the meaning is to continue complication and evolution avoiding extinction and reset). But if we are only to assume 1) then that reset mechanism is not that necessary.

    • If we are to extend 1) point further then we can assume that the “meaning of life” is about pushing as far as possible the meaningless, historically formed structures from the past to the future. And it's about the competition between agents dragging these competing structures into the future (agents are themselves structures). If any ecological niche is free, then its occupation by someone is a foregone conclusion. But which exactly agent-structure will take it would be a matter of chance and the result of competition.
    • Another “meaning of life” may be in the choice between incompatible options for the future: that the probability of replaying any situation tends to zero over time. You could not step twice into the same river. From this point of view, the multiverse does not exist, and the point is to decide what will never happen. If the “meaning of life” is in the impossibility of replaying, then the beginning of time as a simplest structure possible looks logical - there would be no return to that simple state.
    • When trying to create that mentioned minimal model in graphs language (see Section 4) this question transforms to: what is the reason that the start from one vertex is more natural than from several vertices (if it never happens again)?

  3. For simplicity the rules of “structure” changing might be encapsulated to the structure itself (may be atomic parts of the structure can “memorize” rules. How can this be? mind-stuff?, neural networks?). But I guess some meta-rules are inevitable but at least they desired to be derived from the simplest beginning of the Universe assumption and postulates of natural selection. But on the other hand the complete immanence of both rules/laws and meta-laws/meta-rules (when they always have a material carrier) are very attractive concept as it's a simpler one hence it's better from Occam Razor point of view. But I have a guess that immanence of meta-laws leads to the strange loop. But what if the strange loop is a valid building block of the Universe?

    • I have no idea how that complete immanence can be possible,
    • I haven't thought this through so may be the any strange-loop problem can be solved via assuming that the structure can have access not to itself but to itself-in-the-past.

  4. The atomic parts of the graph might be something that is convenient to call “agents” that have an “intention” / “free will” to randomly choose from available actions that change themselves and other agents. So each agent is described by the algorithm that changes it's connected environment/neighborhood and hence changes algorithms (including the algorithm of itself). This swarm of algorithms should be capable of producing more and more complex algorithms via natural selection. This point of view raises at least two questions: (1) of simultaneity, (2) ontology of the material carrier of algorithms. (1): does natural selection need the interactions between the agents and their reproduction to be simultaneous? (2) is closely related the previous item in the list about laws/meta-laws immanence. Or simply algorithms are patterns in the structure that changes in time? I tried to think about Primitive recursive functions, μ-recursive function and Lambda calculus as a candidates for algorithms carriers but had no luck - the task was too hard for me and I felt like I missed something important... Misc:

    • Dualism of the algorithm on the one hand as instructions written into the structure and on the other hand as the executor who reads and executes the instructions. The algorithm assembles a new executor who can read the algorithm – like in DNA,
    • “Space” – is an encoded map of possible actions,
    • How to control access to the environment (the same problem is also present in parallel programming)?
    • “Freedom of will” is the property of the atom of the world,
    • Complex algorithms require isolation of the “internal” from “external” – leads to appearing of “borders” and “shells”,
    • What does “spatial link” mean? I always meant by this the possibility of agent's action-impact. But the “link” can also mean entanglement – restrictions on possible simultaneous states of linked objects. As John Preskill defines it [10]: “we can split a system into parts, and there is some correlation among the parts so I can learn something about one part by observing another part”. How does these two definitions relate to each other? The simplest way to combine them might be to embrace the “Spooky Action at a Distance” (gravity via entanglement theories?) and define entanglement via action-impact links,
    • All my reflections and thinking on computability and recursive functions did not give anything. What if at least partially it's because of the Church–Turing thesis that is a hypothesis about equivalence between the intuitive notion of algorithmic computability and strictly formalized notions of a partially recursive function and a function computable on a Turing machine. So until I get an intuitive grasp about it's main workings it's useless to dig into formalizations,
    • May be there should be a fundamental ontological division into the body of recursion and the base of recursion for which new notations should be introduced to the graph-like stucture.

  5. Spontaneous symmetry breaking might be an important idea regarding random variation in the natural selection. “Spontaneous” might refer to the immanence of intention to the agents. And “symmetry breaking” is necessary for random events to occur: if the symmetry doesn't break then all outcomes/impacts are equivalent and there's no randomness (“All roads lead to Rome”).

  6. At the moment the picture in which we represent the Universe in the form of unstable energy flows (plus “batteries”) is completely ignored in my speculations. But I can't help but think that it's a very convenient point of view and language if we are to think about life and natural selection dynamics. This reminds me about Unmoved mover but it's really a far fetched association.

    • Both energy and information about environment are stored by agents,
    • Life dies when it ceases to be a conductor of energy, living on the difference of energy: it takes energy then uses it to take more energy.

  7. The solvability of the formulated problem is equivalent to the fact that the flow of time is a choice between pre-determined variants. The idea of free will is based on the idea of the pre-existence of a space of options to choose from. It resembles a notion of a flow in intuitionistic mathematics. But this process should not be the same as the flow of real numbers, but it should give the complicating of the individuals-patterns instead.

To sum up:

The notions of recursion, reproduction/doubling, randomness/spontaneous symmetry breaking and natural selection seem to be among the keys to understanding novelty creation and the Universe development from the simplest state at the beginning of time. And what about energy flows?

2.6 Some questions and Chaotic thoughts

≡↑

Chaotic thoughts

There is also a list of thoughts, notes and questions that at some point seemed relevant to me but are such a mess actually:

3. On artificial life, open ended evolution and “why these laws of nature?” question

≡↑

   My main goal briefly and correctly: to create a model of Open Ended Evolution (Then test it on the PC. May be even with hardware random number generator). The good overview of the Open Ended Evolution problem is given by Alastair Channon: channon.net/alastair [9]. This name states for an artificial life that don’t stop it’s evolution on a fixed level of complexity but instead progresses further. The only difference seem to be that the model I’d like to create is planned to be the simplest model. To be the simplest in the philosophical sense. Like Occam’s razor. These restrictions of simplicity make the difficulties that I was describing in this open letter (start from the simplest structure, no predetermined structures except natural selection postulates, no environment, only individuals).

   And the final goal is to answer the “why these laws of nature?” question. More precisely: why these processes take place but not the other. The history in the model of natural selection is a perfect explanation (if we know the whole history) and answer to any “why?” question. But for the model of open ended evolution to be a candidate for a model of the beginning of the universe it should be the simplest model possible (from the philosophical reasoning).

4. The minimum mathematical model for open ended evolution (the more precise description of the mathematical part)

4.1 Possible restrictions and constraints of the model

≡↑

Here is an attempt to describe the restrictions and constraints mentioned in section 3 (and described in more details in the open letter) in a more formal way.

  1. The model describes process of discrete changes of the graph-like structure.

  2. The process starts from the graph consisting of the only one vertex. There are no edges.

  3. The predetermined rules are applied to the existing graph to get the next graph.

  4. The predetermined rules should include the rules that resemble the postulates of natural selection:

    • 4.1 “Reproduction” (may be: spontaneous events of doubling of the vertices)
    • 4.2 “Heredity” (may be: conservation or invariability of some subgraph of the graph. Or subset of the set of edges of a particular vertex)
    • 4.3 “Variation” (may be: spontaneous events of changing the vertices’ edges during reproduction. There are more than one such events so there are random choices in most cases)
    • 4.4 “Selection” (I’m not sure but there also may be the events of joining two vertices into one. May be this event is applied only to the two vertices that share in their history the same event of doubling)

  5. As I see it now the edges of the vertices appear to be the structure of the individuals in the natural selection. But I may be wrong.

  6. The are two ways of imagining this process:

    • 6.1 Do not draw the history of rules application. First step: o, Second step: o―o. Here the rule of reproduction was applied.
    • 6.2 Do draw the history of rules application. First step: o, Second step:

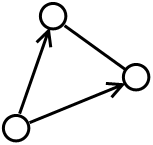    In this picture the history of reproduction was taken into account. And directed edges are used to denote events of application of the rules to the graph (or to the subgraph of it).

  7. During the process of rules application (partially randomly) we get the history of graph changes. The process of creating such a history is an infinite process.

  8. In the history of this process should be patterns in the graph that are isomorphic to each other in some sense. If we are imagining the process like in 6.2 then the isomorphic patterns should be found both in time direction and in graph structure. The simplest analogue to this is the waves propagating in the medium.

  9. Moreover there should be the evolution of such patterns that lead to their complication and incorporation the information about the graph structure or about other patterns. Presumably this evolution is led by competition for “staying alive” of such patterns with each other.

  10. This evolution should not stop at the fixed level of pattern complexity. So it should be the case of Open Ended Evolution.

Presumably, the model to be built should satisfy the 1, 2, 4, 8, 9, 10 constraints. Other constraints may be altered to fit the 1, 2, 4, 8, 9, 10 constraints.

So it's my guess that formal models that satisfy the constraints mentioned can be constructed. But this attempt to describe the constraints is also a request for convincing arguments in favor that the model satisfying the constraints is impossible.

Some notes:

4.2 Examples of the models that resemble the desired model

≡↑

Here is the a try to create a mathematical dynamic model that satisfies some of the constraints mentioned. I doubt that it would succeed. But it may show some problems and make the limitations of this approach more clear.

4.2.1 The first example

≡↑

The decsription of the first model:

  1. The model describes process of discrete changes of the undirected graph structure.
  2. Each vertex has a boolean label “True” or “False”.
  3. The process starts from the graph consisting of the only one vertex. There are no edges. The vertex has a “True” label.
  4. The predetermined rules are applied to the existing graph to get the next graph.
  5. The predetermined rules that are applied simultaneously:
    • 5.1 “Reproduction”. If “parent” vertex’s label is “True” then it reproduces and the “child” vertex is created. The “child” vertex has a “True” label.
    • 5.2 “Variation” + “Heredity”. There is a ½ probability for each edge of “parent” vertex to be in the edges set of “child” vertex.
    • 5.3 “Heredity”. The edge is always created between the “parent” and “child” vertices.
    • 5.4 “Selection”. Forget about the newly created “child” vertices (temporary remove them from the consideration). For each vertex in the reduced graph: If vertex’s label is “True” then for each edge of this vertex the “True” signal is send with ½ probability to the vertex’s neighbors. Then again for each vertex in the reduced graph: If at least one “True” signal came to the vertex then it’s label would be “True” on the next time step. Otherwise is’s label would be “False”.

Let’s draw some steps of this process. “True” vertices would be white. “False” vertices would be black.

  1. Start (numbers distinguish vertices):
    [○1]
  2. Only 5.1, 5.3 and 5.4 were applied (no edges so no “True” signals):
    [●1]――[○2]
  3. There are randomly selected outcomes:
    • 3.1 [○1]――[●2]――[○3]
    • 3.2 [●1]――[●2]――[○3]
    • 3.3 [○1]――[●2]――[○3]
          ┕―――――――┚
    • 3.4 [●1]――[●2]――[○3]
          ┕―――――――┚
  4. There are even more randomly selected outcomes on this step. So the computer simulation is required.

4.2.2 The second example

≡↑

There is another model that is more simple in some sense.

The description of the second model:

  1. The model describes process of discrete changes of the undirected graph structure.
  2. Each vertex has a non-negative integer label (l≥0, l∈ℕ).
  3. The process starts from the graph consisting of the only one vertex. It has only one loop edge that connects vertex to itself (and it counts as one edge). The vertex has a “1” label.
  4. The predetermined rules are applied to the existing graph to get the next graph.
  5. The predetermined rules that are applied in two stages:
    • 5.1 “Individuals and Environment”. For each vertex in the graph: if vertex’s label is positive integer n then n times do the following: the “1” signal is send to an edge that is randomly selected from the vertex’s edges set (including the edge to itself). If the vertex has m edges then the probability is 1/m. Actually the signal is sent to the vertex’s neighbors. Then again for each vertex in the graph: if n signals came to the vertex then it’s label is set to “n”. It can be “0”.
    • 5.2 “Reproduction”. For each vertex in the graph (“parent” vertices): if “parent” vertex’s label is positive integer then it reproduces and the “child” vertex is created. The “child” vertex has a “1” label. The edge that connects “child” vertex to itself is always created.
    • 5.3 “Variation and Heredity”. For each “child” vertex in the graph: If signal came from “X” vertex to “parent” vertex then the “child” vertex has an edge to the “X” vertex.
    • 5.4 “Selection”. For each vertex in the graph: If vertex’s label is “0” then the vertex is removed from the graph together with all it’s edges.

Let’s draw some steps of this process. First number distinguish vertices, ∩ reminds on the self edge, ↕ shows that the signal is sent along the self edge, last number is a label:

Seems like the weighted edges are required… There are more randomly selected outcomes on this step. So the computer simulation is required to speed up the research.

5. Why this task? On “Why is there something rather than nothing?” question

≡↑

   The two described tasks (1. to get laws of nature from natural selection of structures. 2. to create the minimum mathematical model for open ended evolution) are actually the same task.

   The minimal open ended evolution model (OEE model) that are to be created should be capable of producing at its future steps the invariant behavior of really huge number of individuals. And this invariant behavior may be called the laws of nature. I have doubts that we will ever have enough computational power to run the simulation long enough to get this invariant behavior. But who knows?

   Actually I have a guess (that is to be checked) that if this minimum OEE model exists then it’s really a simple one. It should have a simple structure, but it’s not easy to formulate it right. It’s like the postulates of natural selection: they are obvious, but until they were formulated it was really hard to assume them.

   And this model is a request from philosophy. It’s actually a philosophical mathematics that uses physics and natural selection theory for inspiration. It’s a task to create explanation framework that answers any “why questions” in the same way that theory of evolution answers lots of why questions on origin of different life forms. If this explanation framework exist then it should answer the ancient question “Why is there something rather than nothing?”. It is rather strange to use laws of nature to answer this question. It’s like a joke about creationist-evolutionist debate: “The God created all the evidence of the evolution”, says creationist. Then the evolutionist replies: “It’s the same as to assume that the God created the world this morning. And he has created me already unshaven”. So all pre-existing structures need explanation (including laws of nature). My current guess is that the model I started to build in chapter 4 “The minimum mathematical model for open ended evolution (the more precise description of the mathematical part)” lacks something like the “Law of habit” by Charles Peirce or the “Principle of Precedence” by Lee Smolin.

UPD. Examples of models from section 4 have highlighted the need for a more consistent justification of the original rules for modifying the graph.

6. Infinite elephants, indeterminism vs. determinism, "why?" answering theories vs. "how?" answering theories

≡↑

The desired model assumes indeterminism. And I actually have some consideration why determinism is wrong. For this we need to remember some ancient Greeks and the law of gravitation. Some of them formulated the law as “everything falls down”. And immediately were faced with the question “Why does not the ground then fall down?”. And they gave the answer “It is standing on the elephant”. On a reasonable next question “Why does not the elephant fall down?” they gave the answer “The elephant is standing on another elephant”. On reasonable “WTF???” they gave an answer “There are infinite number of elephants”. And then they came to a bizzare picture with an infinite number of elephants. Then some cleverer ancient Greek reformulated the law as “everything falls to the ground” - and removed the infinite chain of elephants. As we found out, he was right.

If we are to explain history and answer “why?” questions we either should embrace countably infinite causal chains that go to the past or to have finite causal chains that go to the past but with randomness that creates novelty. The latter is better from Ockham’s razor point of view. I'm already under assumption that countably infinite is better than uncountably infinite from Ockham’s razor point of view.

As said in Section 3 the desired model is a perfect candidate for theory that answers any “why?” questions. But that's not the case for your typical physics theory: it assumes lots of complex mathematical objects to be present without explanation how they emerged. So it's like postulating an elephant in example above - except that the theories were tested against reality and they precisely describe how processes work. If we would create yet another theory that postulates some complex mathematical objects we still would need an answer to “why these objects?” question. So the right way of answering “why?” questions should be aware of the described problem right from the start - something like self-justifying comes to mind (whatever that means). This inevitably raises meta-laws question that mentioned in Section 2.5 so even the desired model still doesn't have a complete answer to this problem (actually this acticle has much more questions than answers...).

7. Artificial life model as a self-justifying theory of everything

≡↑

7.1 redirect to 7

7.2 redirect to Introduction 4

7.3 redirect to Introduction 5

≡↑

THIS SECTION #7. IS OUTDATED: I'M NO LONGER FOND OF SELF-JUSTIFICATION IDEA.

First I'll add some details about notion of self-justifying that show more about the motivation behind the research. Potential theories of everything can be self-justifying or not. It means that the theory is:

  1. theory of everything: capable of answering all questions like "why these structures exist / processes take place instead of the other ones?". I.e. given all knowledge about the past they can (at least theoretically) track chains of causes back to the past to the moments where they came to existence.
  2. self-justifying: capable of answering question "why the theory of everything works this way not another?". And answer "because it's predictions are in agreement with experiments" is not enough because there can be infinite number of such theories that differ in things we cannot test (yet? never? who knows...). So we can either wait for General relativity + Quantum mechanics unification (and see if there would be the same problem :) or we can try to answer this question via self-justifying. It relies on philosophical necessity, Occam's razor, Captain Obvious considerations and common sense.

As far as I know candidates for theory of everything that are being developed by physicists are not meant to be build self-justifying. But in the past the self-justifying cosmogonies were build. The simplest one starts from the sentient god-creator. The god was at the beginning of time and he is self-justifying. It can be imagined as the Universe starts with artificial general intelligence agent with goals. Then AGI creates everything else...

I suggest use similar approach but use natural selection instead of AGI. We know that biological natural selection is capable of producing sentient individuals and it's simpler than AGI from Occam's razor point of view. This assumes that the fundamental aspect of the Universe if the life (instead of AGI/god or predefined mechanical-like laws).

8. P.S.

≡↑

I'm absolutely serious in spite of the fact that the title was borrowed from the comedy science fiction novel by Douglas Adams. I only think that it's useful to remember that you are looking for an answer to The Ultimate Question of Life, the Universe, and Everything if you are really looking for it. My intuition suggests that the answer can be found in the direction described in this article. Even if it can't be found in that direction then considerations why it can't be would still be a great help to find the answer.

I would be grateful for any feedback and advice.

9. References

≡↑

[1] Lee Smolin, The fate of black hole singularities and the parameters of the standard models of particle physics and cosmology, arXiv:gr-qc/9404011v1, 1994, arxiv.org/abs/gr-qc/9404011

[2] Lee Smolin, Temporal naturalism, arXiv:1310.8539, 2013, arxiv.org/abs/1310.8539

[3] Christoph Adami, Information-theoretic Considerations Concerning the Origin of Life, Origins of Life and Evolution of Biospheres 45 (2015) 309-317, adamilab.msu.edu/chris-adami

[4] Francis Heylighen, Blind Variation and Selective Retention, Principia Cybernetica Web, 1993, pespmc1.vub.ac.be/BVSR.html

[5] William Kingdon Clifford, On the Space-Theory of Matter, 1876, en.wikisource.org/wiki/On_the_Space-Theory_of_Matter

[6] Frank Wilczek, Beautiful Losers: Kelvin’s Vortex Atoms, 2011, pbs.org/wgbh/nova/blogs/physics/2011/12/beautiful-losers-kelvins-vortex-atoms

[7] S.O. Bilson-Thompson, A Topological Model of Composite Preons, arXiv:hep-ph/0503213, 2005 preprint, arxiv.org/abs/hep-ph/0503213

[8] S.O. Bilson-Thompson, F. Markopoulou, and L. Smolin, Quantum Gravity and the Standard Model, arXiv:hep-th/0603022, 2007, arxiv.org/abs/hep-th/0603022

[9] Alastair Channon page that has the description of Open-ended evolution, channon.net/alastair

[10] Jennifer Ouellette, How Quantum Pairs Stitch Space-Time quantamagazine.org/tensor-networks-and-entanglement-20150428

Return to root