A GPU implementation of L-BFGS-B (cuLBFGSB)
cuLBFGSB is an open-source library for the GPU-implementation (with NVIDIA CUDA) of the nonlinear optimization algorithm named the limited memory Broyden-Fletcher-Goldfarb-Shanno with boundaries (L-BFGS-B). It is cross-platform (Windows and Linux) and licensed under the Mozilla Public License v. 2.0.
It has been recently tested with CUDA 12.0.
This library contains both the L-BFGS-B implementation on the GPU (with CUDA) and the original implementation on the CPU. It also includes a simple example code that solves the steady-state combustion problem (dsscfg) in MINPACK-2 (https://en.wikipedia.org/wiki/MINPACK) test to both the CPU and the CUDA version of L-BFGS-B.
We would like to hear from you if you appreciate this work.
It is an updated implementation of the paper Parallel L-BFGS-B algorithm on GPU ( refer to our project page for more details: http://yunfei.work/lbfgsb/lbfgsb_tech_report.pdf ). For the original version that contains a solver to the CVD problem, please refer to http://yunfei.work/lbfgsb_gpu.zip .
Additionally, we provide a pre-compiled library for Windows x64 platform using CUDA 11.2. You may download the compiled library from: http://yunfei.work/lbfgsb/culbfgsb_compiled_CUDA_11_2_win64.zip , which contains both the DLL and the static library.
Remark: the current version supports a fixed size of Hessian approximation m == 8, which has been sufficient for most applications.
Performance
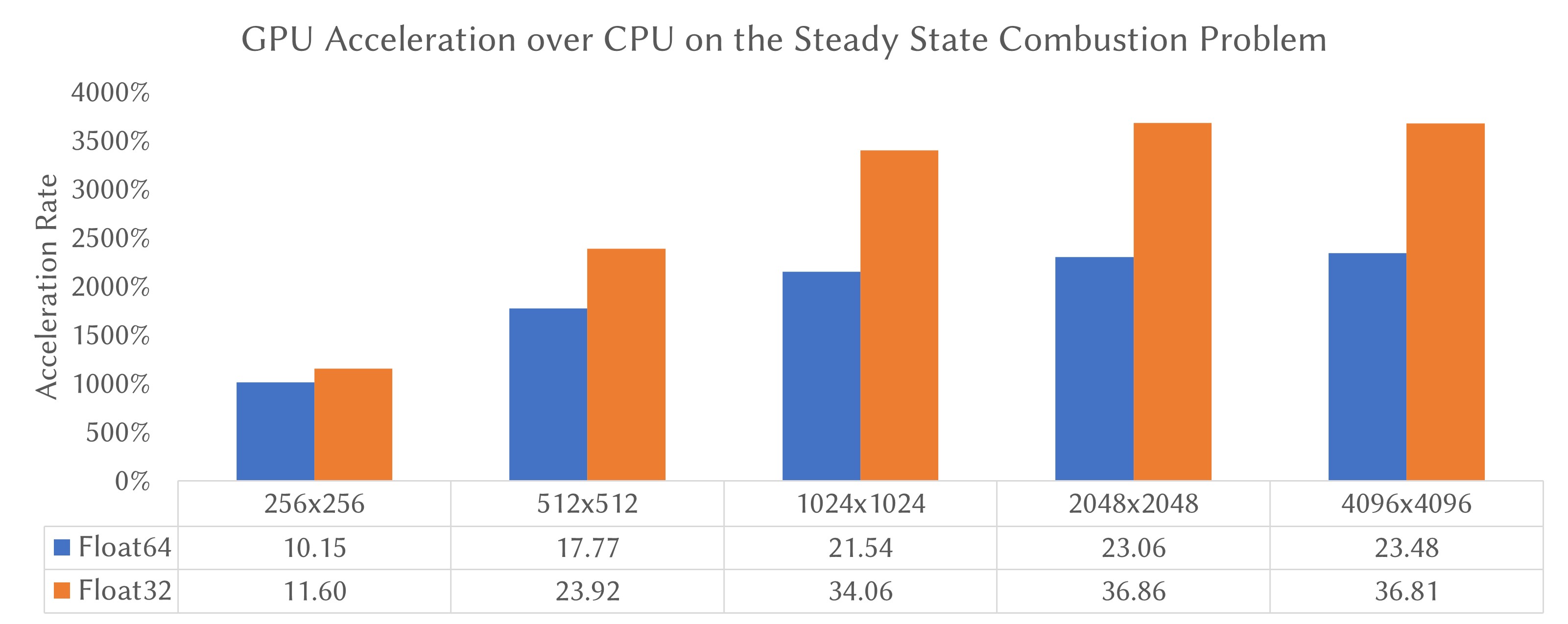
In the figure above, we summarize the acceleration rate on the steady-state combustion problem with both single (32-bit) and double (64-bit) floating precision and over various sizes of discretization (from 256x256 to 4096x4096). The test platform has an Intel Core i9-9900K CPU @ 3.60GHz and an NVIDIA GeForce RTX 2080Ti as the GPU. The acceleration rate ranges from 10.15x (float64, 256x256) to 36.86x (float32, 2048x2048).
Compilation
To compile cuLBFGSB, you'll need CMake or CMake-GUI (https://cmake.org), and the CUDA toolkit (https://developer.nvidia.com/cuda-downloads) installed before compilation.
Command Line:
- make a directory, say, build, with mkdir build, enter the build directory, type cmake ..
- Optionally you can adjust the options with ccmake .. In some cases, there can be some packages that CMake cannot find. You need to specify their paths through ccmake manually.
- type make to compile the code. For speeding up the compilation process, you may use make -j.
CMake-GUI:
- open CMake-GUI, enter the correct directory for source code, and build. Then click Configure, choose your installed version of the compiler (on Windows, choose the correct version of Microsoft Visual Studio).
- after configuration, you should have all the libraries automatically found (without notifications of errors). Otherwise, please check the Advanced box and specify those missing header paths and libraries manually.
- click generate to generate the makefile (on Windows, the generated file is a Visual Studio solution).
- compile the library and run the test example (dsscfg).
- by default, the compiled library is statically-linked. You may turn on the BUILD_CULBFGSB_SHARED switch in CMake to compile a shared library.
Usage
To use the library in another project, you may include culbfgsb.h and link with the compiled library (either the static version or the shared one). In the code, you may firstly initialize a LBFGSB_CUDA_OPTION, with mode set to either LCM_NO_ACCELERATION (CPU version) or LCM_CUDA (GPU version).
LBFGSB_CUDA_OPTION<real> lbfgsb_options;
lbfgsbcuda::lbfgsbdefaultoption<real>(lbfgsb_options);
lbfgsb_options.mode = LCM_CUDA;
lbfgsb_options.eps_f = static_cast<real>(1e-8);
lbfgsb_options.eps_g = static_cast<real>(1e-8);
lbfgsb_options.eps_x = static_cast<real>(1e-8);
lbfgsb_options.max_iteration = 1000;where real is the template parameter (can be either float or double), eps_f, eps_g, and eps_x are the criterion for convergence based on the function value, the gradient norm, and the movement of solution (by default 1e-15); and max_iteration specifies the maximal number of iterations (by default 1000) of the optimization.
Then you may initialize an LBFGSB_CUDA_STATE, with CUBLAS handle also initialized.
LBFGSB_CUDA_STATE<real> state;
memset(&state, 0, sizeof(state));
cublasStatus_t stat = cublasCreate(&(state.m_cublas_handle));The state.m_funcgrad_callback should be set to a callback function that has the following declaration:
int callback_function(real* x, real& f, real* g, const cudaStream_t& stream, const LBFGSB_CUDA_SUMMARY<real>& summary);where x is an input vector for the current solution, f is an output value that you'd compute the function value based on x (i.e., f(x)), g is an output vector that you'd compute the gradient of f over x (i.e., g = df(x)/dx), stream is the CUDA stream handle, and summary is the summary of current state of the L-BFGS-B solver.
For the CUDA version of L-BFGS-B, x, g should be pointers to the device memory, while f is always a single scalar on the main memory.
Then you'd initialize the buffers (buffers on the main memory for the CPU version, or buffers on the device memory for the CUDA version) for x, g, xl, xu, and nbd, where xl and xu are the lower and upper bound of the solution, nbd is the number of boundaries of each dimension of x (i.e., nbd[i] = 0 indicates the i-th element of x is unbounded, nbd[i] = 1 indicates the lower bound is imposed for the i-th element of x, and nbd[i] = 2 indicates both the upper and lower boundaries are imposed).
You'd also initialize x by yourself to give x a reasonable beginning state.
Finally, you may call lbfgsbcuda::lbfgsbminimize to perform optimization, which would call the state.m_funcgrad_callback function on each step of the optimization.
For more details, please check the dsscfg example in the repository.
BibTex Citation
@article{fei2014parallel,
title={Parallel L-BFGS-B algorithm on gpu},
author={Fei, Yun and Rong, Guodong and Wang, Bin and Wang, Wenping},
journal={Computers \& graphics},
volume={40},
pages={1--9},
year={2014},
publisher={Elsevier}
}