SparseBlockJacobians.jl

This project offers tools to help calculating Jacobians from large and sparse models. We assume a transposed CSC matrix, where the columns are the partial derivatives from each residue term. This means we only store in memory the values that are relevant for each residue term, in consecutive chunks of memory. Different formulas can be provided to define different blocks of the Jacobian. The tool handles assembling the complete sparse matrix from the separate blocks. The final complete Jacobian should be suitable for utilization with conventional non-linear least-squares optimization tools.

This project can be seen as an alternative to graph optimization tools such as g2o, where the Jacobian is not usually produced as a concrete object. We seek to enable the definition of large and structured models, while at the same time trying to retain compatibility with more traditional non-linear optimization tools by producing an actual (sparse) Jacobian matrix object in memory.

Figure 1 below shows an example of a regularization problem solved with increasing values for the regularization parameter, producing a classic "L-shaped curve" or "knee curve". The residues from the objective function were calculated with the help from our tool. See examples/simple_regularization.jl.

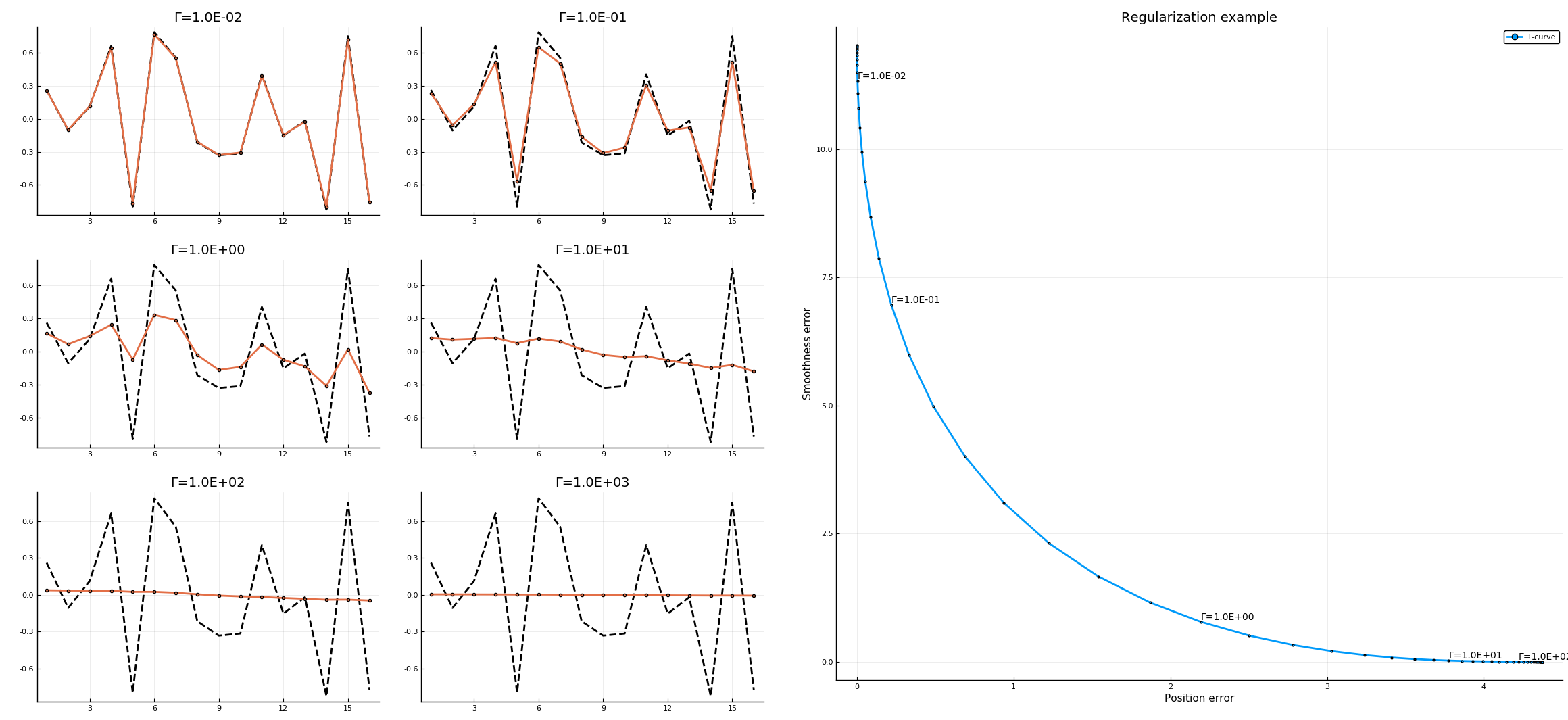
Figure 1: Regularization problem example.