graphblas-algorithms is a collection of GraphBLAS algorithms written using python-graphblas. It may be used directly or as an experimental backend to NetworkX.

Why use GraphBLAS Algorithms? Because it is fast, flexible, and familiar by using the NetworkX API.

Are we missing any algorithms that you want? Please let us know!

Installation

conda install -c conda-forge graphblas-algorithms

pip install graphblas-algorithms

Basic Usage

First, create a GraphBLAS Matrix.

import graphblas as gb

M = gb.Matrix.from_coo(
  [0, 0, 1, 2, 2, 3],
  [1, 3, 0, 0, 1, 2],
  [1., 2., 3., 4., 5., 6.],
  nrows=4, ncols=4, dtype='float32'
)

Next wrap the Matrix as ga.Graph.

import graphblas_algorithms as ga

G = ga.Graph(M)

Finally call an algorithm.

hubs, authorities = ga.hits(G)

When the result is a value per node, a gb.Vector will be returned. In the case of HITS, two Vectors are returned representing the hubs and authorities values.

Algorithms whose result is a subgraph will return ga.Graph.

Plugin for NetworkX

Dispatching to plugins is a new feature in Networkx 3.0. When both networkx and graphblas-algorithms are installed in an environment, calls to NetworkX algorithms can be dispatched to the equivalent version in graphblas-algorithms.

Dispatch Example

import networkx as nx
import graphblas_algorithms as ga

# Generate a random graph (5000 nodes, 1_000_000 edges)
G = nx.erdos_renyi_graph(5000, 0.08)

# Explicitly convert to ga.Graph
G2 = ga.Graph.from_networkx(G)

# Pass G2 to NetworkX's k_truss
T5 = nx.k_truss(G2, 5)

G2 is not a nx.Graph, but it does have an attribute __networkx_plugin__ = "graphblas". This tells NetworkX to dispatch the k_truss call to graphblas-algorithms. This link connection exists because graphblas-algorithms registers itself as a "networkx.plugin" entry point.

The result T5 is a ga.Graph representing the 5-truss structure of the original graph. To convert to a NetworkX Graph, use:

T5.to_networkx()

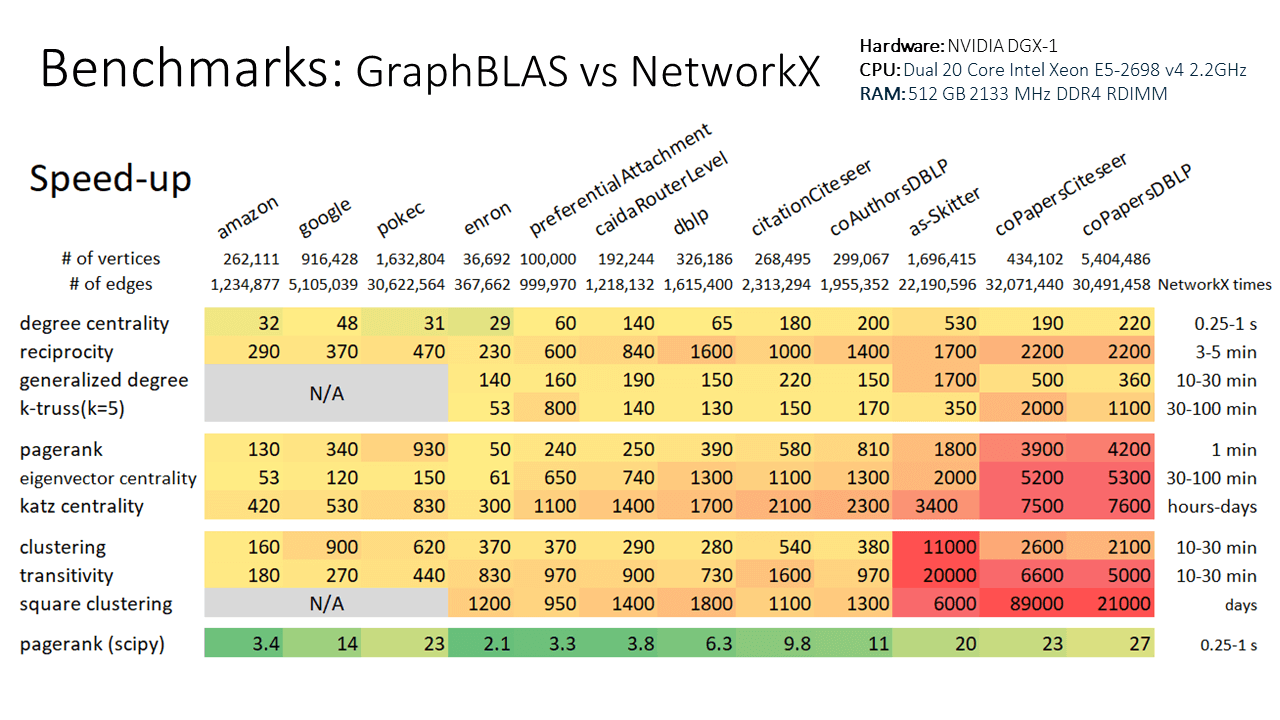
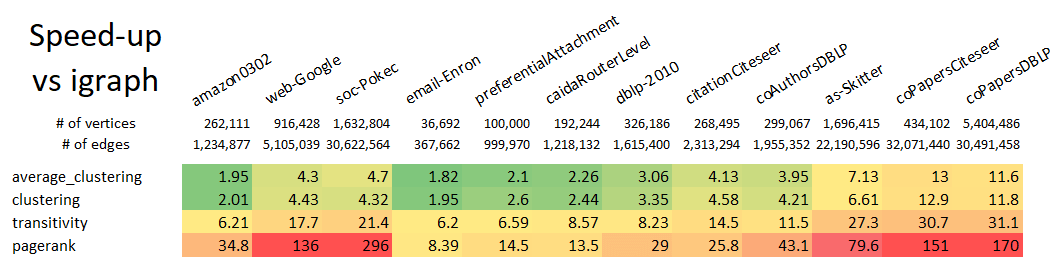
Note that even with the conversions to and from ga.Graph, this example still runs 10x faster than using the native NetworkX k-truss implementation. Speed improvements scale with graph size, so larger graphs will see an even larger speed-up relative to NetworkX.

Plugin Algorithms

The following NetworkX algorithms have been implemented by graphblas-algorithms and can be used following the dispatch pattern shown above.

graphblas_algorithms.nxapi
├── boundary
│   ├── edge_boundary
│   └── node_boundary
├── centrality
│   ├── degree_alg
│   │   ├── degree_centrality
│   │   ├── in_degree_centrality
│   │   └── out_degree_centrality
│   ├── eigenvector
│   │   └── eigenvector_centrality
│   └── katz
│       └── katz_centrality
├── cluster
│   ├── average_clustering
│   ├── clustering
│   ├── generalized_degree
│   ├── square_clustering
│   ├── transitivity
│   └── triangles
├── community
│   └── quality
│       ├── inter_community_edges
│       └── intra_community_edges
├── components
│   ├── connected
│   │   ├── is_connected
│   │   └── node_connected_component
│   └── weakly_connected
│       └── is_weakly_connected
├── core
│   └── k_truss
├── cuts
│   ├── boundary_expansion
│   ├── conductance
│   ├── cut_size
│   ├── edge_expansion
│   ├── mixing_expansion
│   ├── node_expansion
│   ├── normalized_cut_size
│   └── volume
├── dag
│   ├── ancestors
│   └── descendants
├── dominating
│   └── is_dominating_set
├── efficiency_measures
│   └── efficiency
├── generators
│   └── ego
│       └── ego_graph
├── isolate
│   ├── is_isolate
│   ├── isolates
│   └── number_of_isolates
├── isomorphism
│   └── isomorph
│       ├── fast_could_be_isomorphic
│       └── faster_could_be_isomorphic
├── linalg
│   ├── bethehessianmatrix
│   │   └── bethe_hessian_matrix
│   ├── graphmatrix
│   │   └── adjacency_matrix
│   ├── laplacianmatrix
│   │   ├── laplacian_matrix
│   │   └── normalized_laplacian_matrix
│   └── modularitymatrix
│       ├── directed_modularity_matrix
│       └── modularity_matrix
├── link_analysis
│   ├── hits_alg
│   │   └── hits
│   └── pagerank_alg
│       ├── google_matrix
│       └── pagerank
├── lowest_common_ancestors
│   └── lowest_common_ancestor
├── operators
│   ├── binary
│   │   ├── compose
│   │   ├── difference
│   │   ├── disjoint_union
│   │   ├── full_join
│   │   ├── intersection
│   │   ├── symmetric_difference
│   │   └── union
│   └── unary
│       ├── complement
│       └── reverse
├── reciprocity
│   ├── overall_reciprocity
│   └── reciprocity
├── regular
│   ├── is_k_regular
│   └── is_regular
├── shortest_paths
│   ├── dense
│   │   ├── floyd_warshall
│   │   ├── floyd_warshall_numpy
│   │   └── floyd_warshall_predecessor_and_distance
│   ├── generic
│   │   └── has_path
│   ├── unweighted
│   │   ├── all_pairs_shortest_path_length
│   │   ├── single_source_shortest_path_length
│   │   └── single_target_shortest_path_length
│   └── weighted
│       ├── all_pairs_bellman_ford_path_length
│       ├── bellman_ford_path
│       ├── bellman_ford_path_length
│       ├── negative_edge_cycle
│       └── single_source_bellman_ford_path_length
├── simple_paths
│   └── is_simple_path
├── smetric
│   └── s_metric
├── structuralholes
│   └── mutual_weight
├── tournament
│   ├── is_tournament
│   ├── score_sequence
│   └── tournament_matrix
├── traversal
│   └── breadth_first_search
│       ├── bfs_layers
│       └── descendants_at_distance
└── triads
    └── is_triad