tensorgrad

Tensorgrad is a library for visualizing symbolic differentiation through tensor networks.

Tensor network diagrams, also known as Penrose graphical notation or tensor diagram notation, provide a powerful visual representation for tensors and their contractions. Introduced by Roger Penrose in 1971, these diagrams have become widely used in various fields such as quantum physics, multilinear algebra, and machine learning. They allow complex tensor equations to be represented in a way that makes the structure of the contraction clear, without cluttering the notation with explicit indices.

Basics

The Tensor Cookbook (draft) contains everything you need to know about tensor networks.

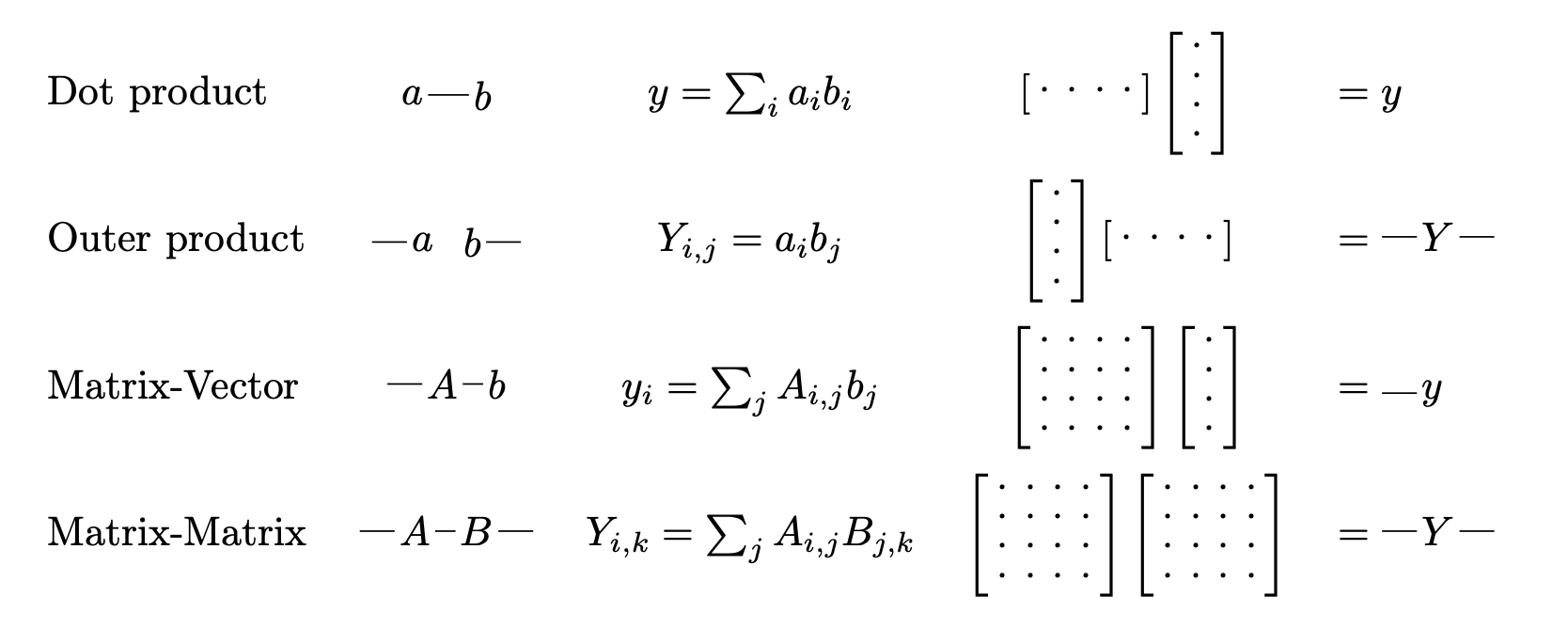
For a beautiful introduction to tensor networks, see also Jordan Taylor's blog post

Example of Tensorgrad

To run the examples for yourself, you can use the main.py file or this colab notebook.

Derivative of L2 Loss

from tensorgrad import Variable
import tensorgrad.functions as F
# ||Ax - y||_2^2
b, x, y = sp.symbols("b x y")
X = tg.Variable("X", b, x)
Y = tg.Variable("Y", b, y)
W = tg.Variable("W", x, y)
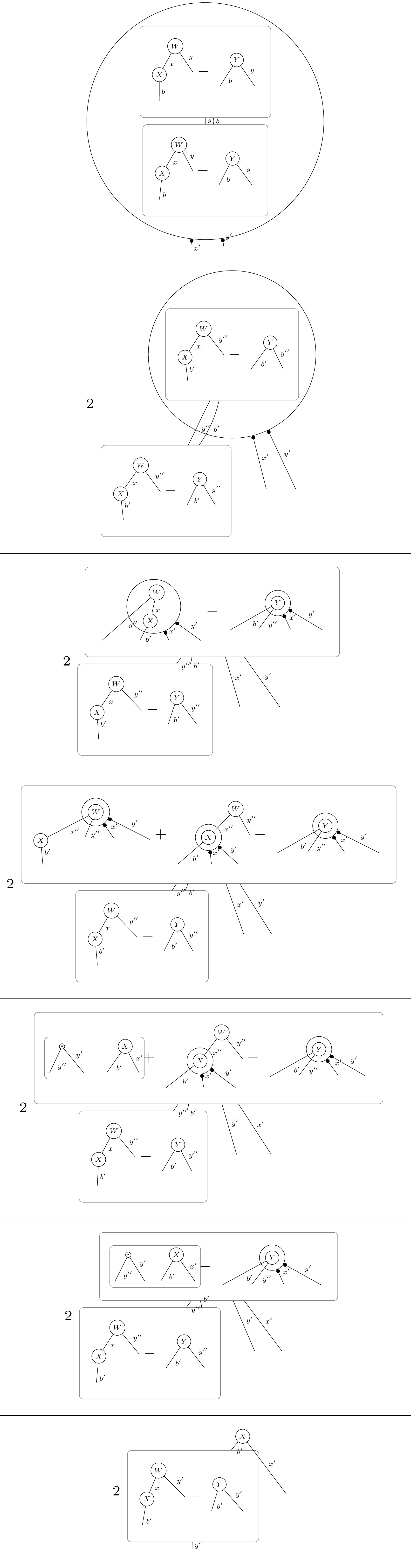
XWmY = X @ W - Y
l2 = XWmY @ XWmY
grad = l2.grad(W)
display_pdf_image(to_tikz(grad.full_simplify()))

This will output the tensor diagram:

Tensorgrad can also output pytorch code for numerically computing the gradient with respect to W:

>>> to_pytorch(grad)
import torch
WX = torch.einsum('xy,bx -> by', W, X)
subtraction = WX - Y
X_subtraction = torch.einsum('bx,by -> xy', X, subtraction)
final_result = 2 * X_subtraction

Hessian of CE Loss

For a more complicated example, consider the following program for computing the Entropy of Cross Entropy Loss:

from tensorgrad import Variable
import tensorgrad.functions as F

logits = Variable("logits", ["C"])
target = Variable("target", ["C"])

e = F.exp(logits)
softmax = e / F.sum(e)
ce = -F.sum(target * F.log(softmax))

H = ce.grad(logits).grad(logits)

display_pdf_image(to_tikz(H.full_simplify()))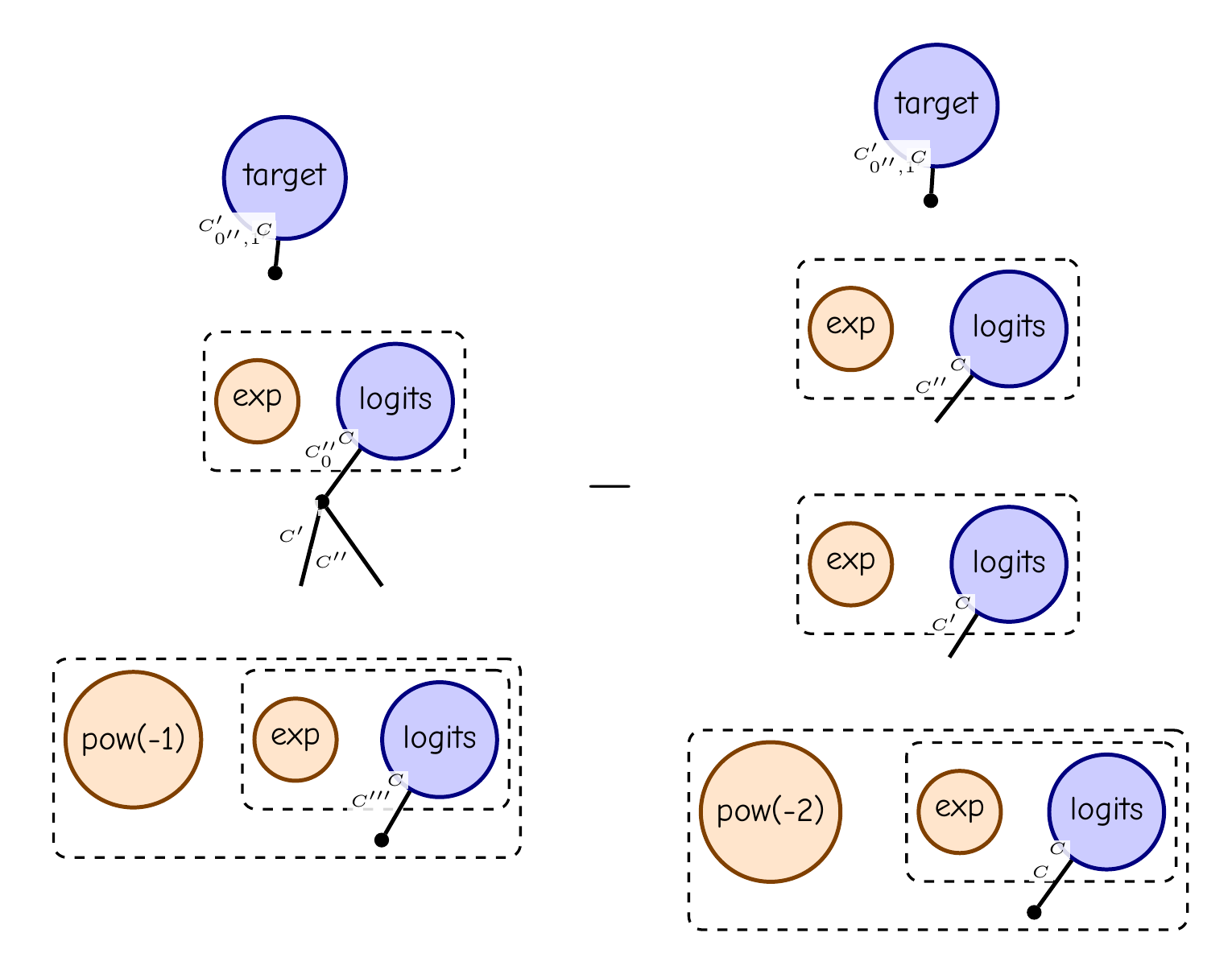

This is tensor diagram notation for (diag(p) - pp^T) sum(target), where p = softmax(logits).

Expectations

Tensorgrad can also take expectations of arbitrary functions with respect to Gaussian tensors.

As an example, consider the L2 Loss program from before:

X = Variable("X", "b, x")
Y = Variable("Y", "b, y")
W = Variable("W", "x, y")
mu = Variable("mu", "x, y")
C = Variable("C", "x, y, x2, y2")
XWmY = X @ W - Y
l2 = F.sum(XWmY * XWmY)
E = Expectation(l2, W, mu, C)
display_pdf_image(to_tikz(E.full_simplify()))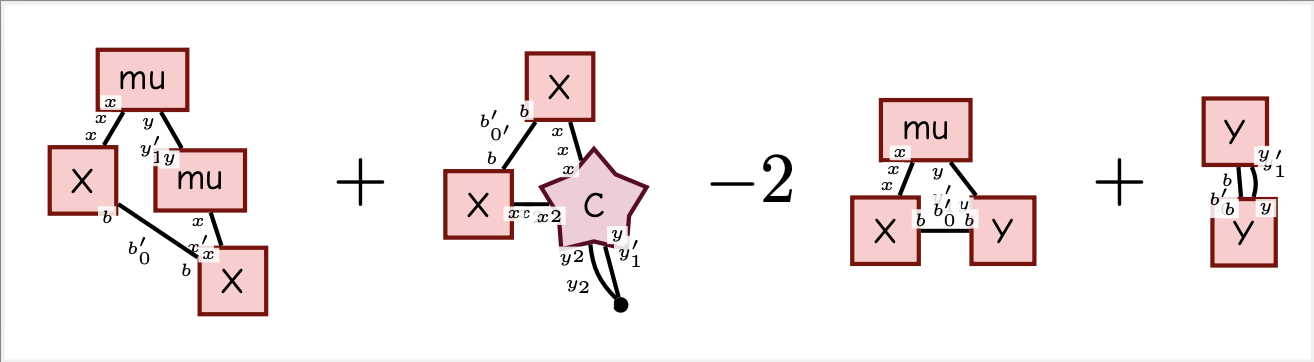

Note that the covariance is a rank-4 tensor (illustrated with a star) since we take the expectation with respect to a matrix. This is different from the normal "matrix shaped" covariance you get if you take expectation with respect to a vector.

Evaluation

Tensorgrad can evaluate your diagrams using Pytorch Named Tensors. It uses graph isomorphism detection to eliminated common subexpressions.

Code Generation

Tensorgrad can convert your diagrams back into pytorch code. This gives a super optimized way to do gradients and higher order derivatives in neural networks.

Matrix Calculus

In Penrose's book, The Road to Reality: A Complete Guide to the Laws of the Universe, he introduces a notation for taking derivatives on tensor networks. In this library we try to follow Penrose's notation, expanding it as needed to handle a full "chain rule" on tensor functions.

Another source of inspiration was Yaroslav Bulatov's derivation of the hessian of neural networks:

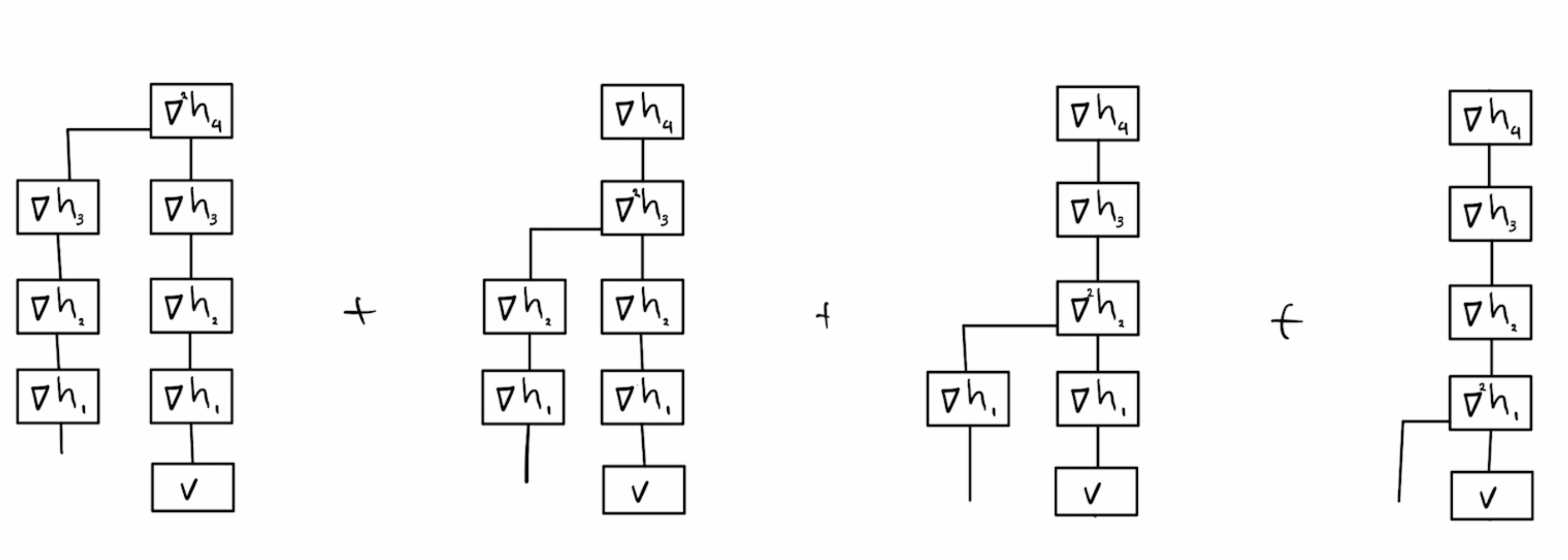
Transformers

Convolutional Neural Networks

The main ingredient in CNNs are the linear operations Fold and Unfold. Unfold takes an image, with dimensions HxW and outputs P "patches" of size K^2, where K is the kernel size. Fold is the reverse operation. Since they are linear operations (they consists only of copying/adding) we can express them as a tensor with shape (H, W, P, K^2).

Hayashi et al. show that if you define a tensor (∗)_{i,j,k} = [i=j+k], then the "Unfold" operator factors along the spacial dimensions, and you can write a bunch of different convolutional neural networks easily as tensor networks:

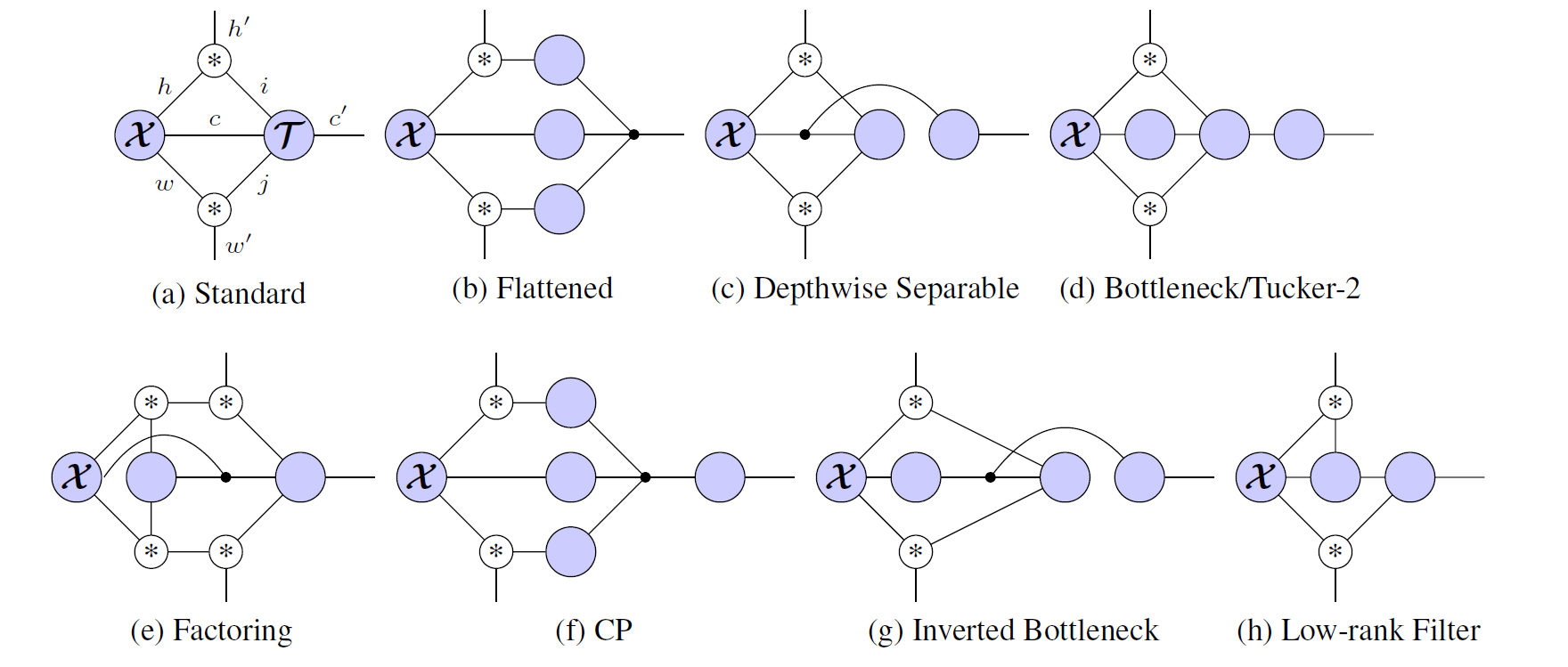
With tensorgrad you can write the "standard" convolutional neural network like this:

data = Variable("data", ["b", "c", "w", "h"])
unfold = Convolution("w", "j", "w2") @ Convolution("h", "i", "h2")
kernel = Variable("kernel", ["c", "i", "j", "c2"])
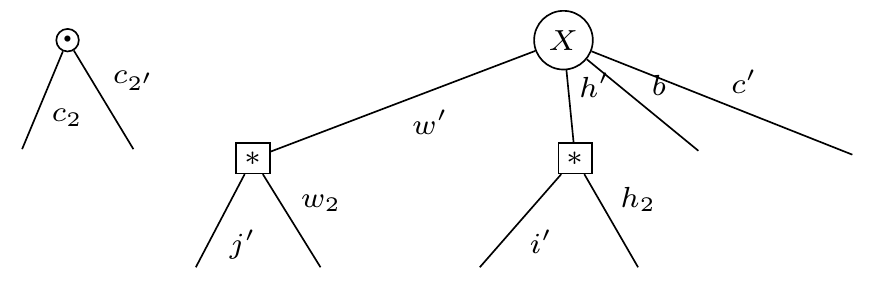
expr = data @ unfold @ kernel

And then easily find the jacobian symbolically with expr.grad(kernel):

Tensor Sketch

Taken from this Twitter thread: I wish I had know about Tensor Graphs back when i worked on Tensor-sketching. Let me correct this now and explain dimensionality reduction for tensors using Tensor Networks:

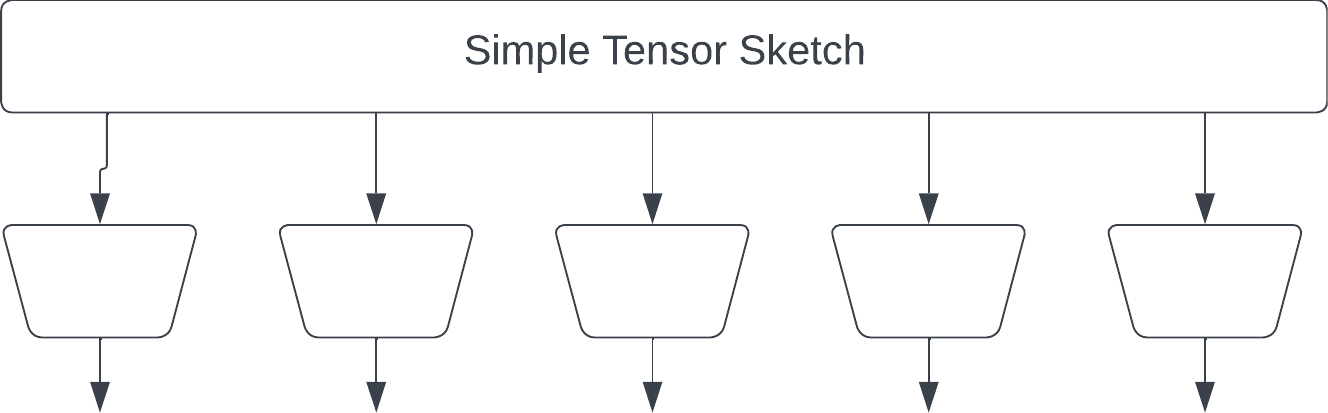
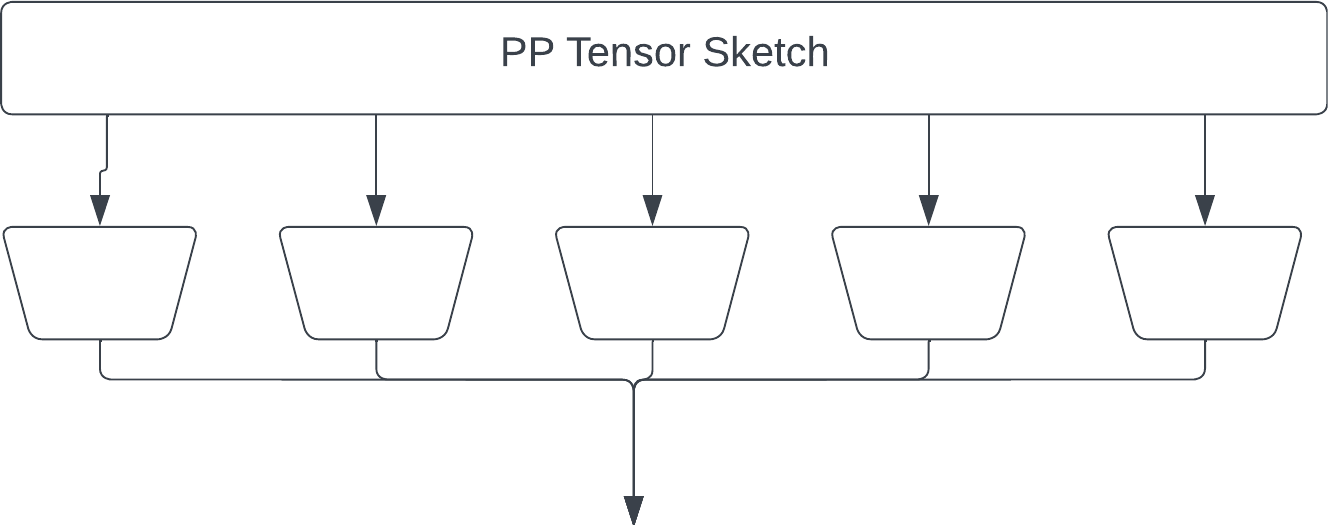
The second version is the "original" Tensor Sketch by Rasmus Pagh and Ninh Pham. (https://rasmuspagh.net/papers/tensorsketch.pdf) Each fiber is reduced by a JL sketch, and the result is element-wise multiplied. Note the output of each JL is larger than in the "simple" sketch to give the same output size.

Next we have the "recursive" sketch by myself and coauthors in https://thomasahle.com/#paper-tensorsketch-joint. In the paper we sometimes describe this as a tree, but it doesn't really matter. We just had already created the tree-graphic when we realized.

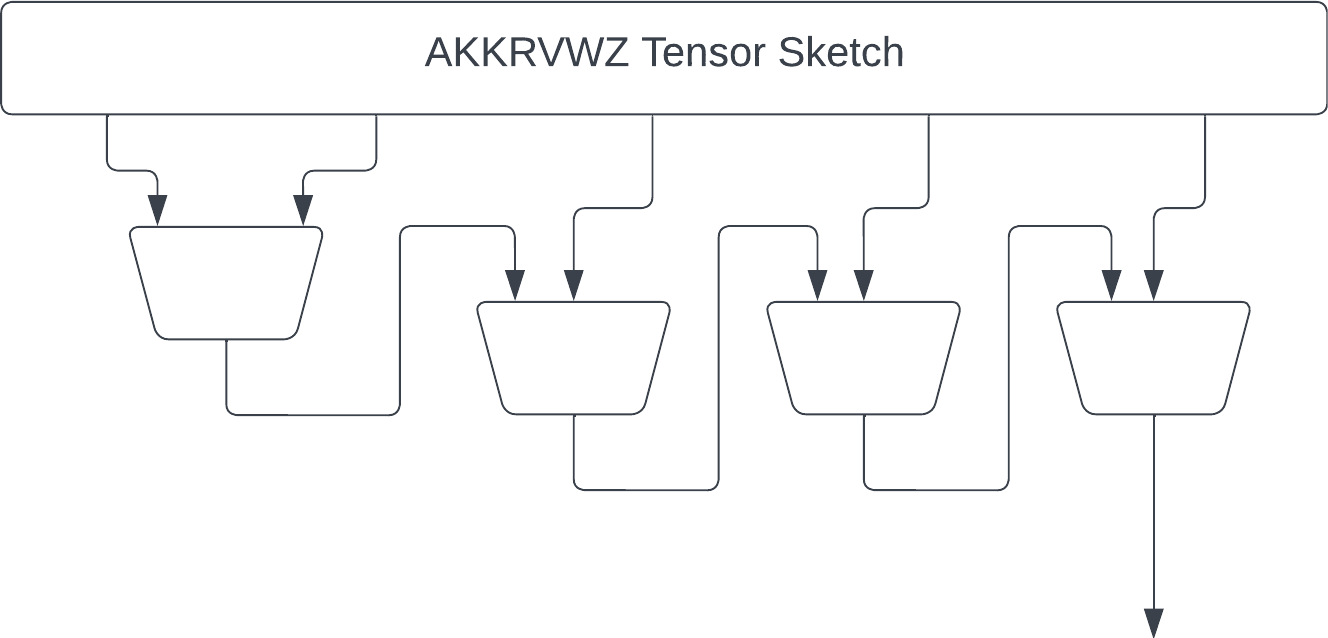
The main issue with the AKKRVWZ-sketch was that we used order-3 tensors internally, which require more space/time than simple random matrices in the PP-sketch. We can mitigate this issue by replacing each order-3 tensor with a simple order-2 PP-sketch.

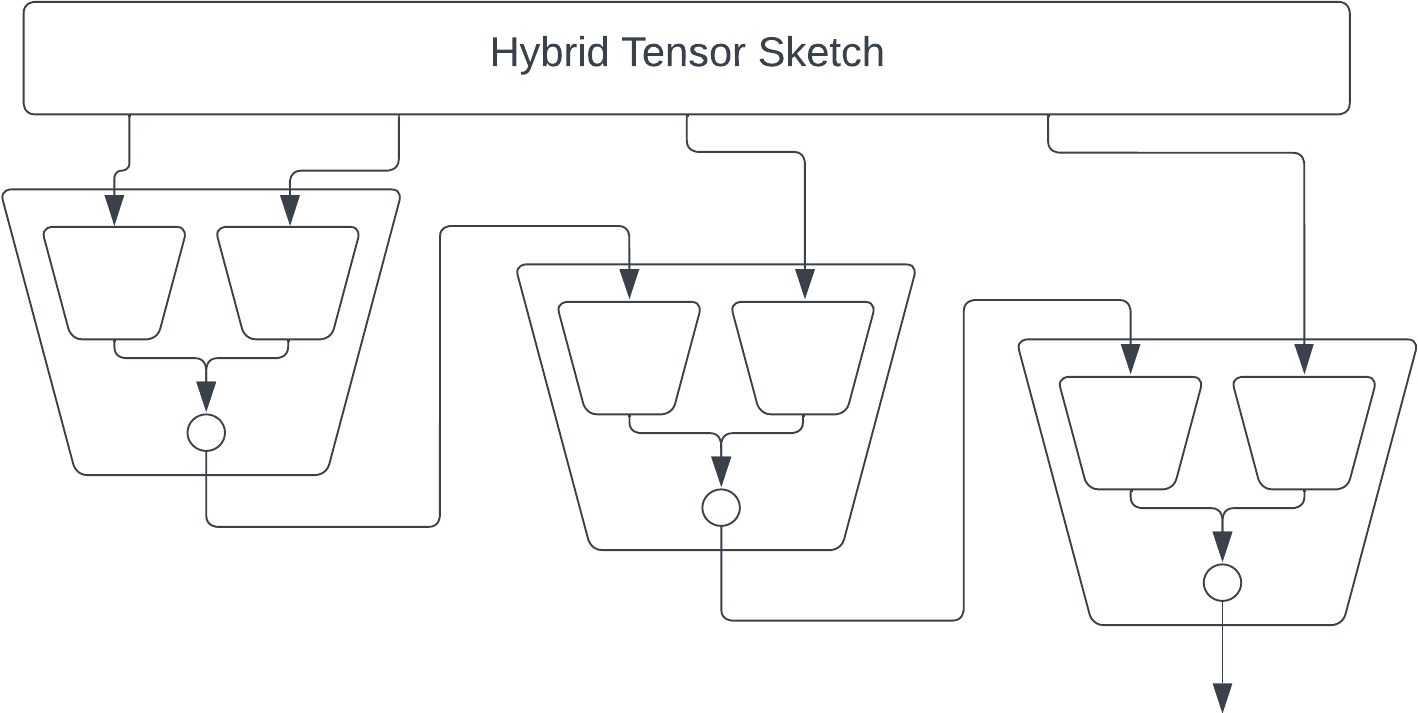
Finally we can speed up each matrix multiplication by using FastJL, which is itself basically an outer product of a bunch of tiny matrices. But at this point my picture is starting to get a bit overwhelming.

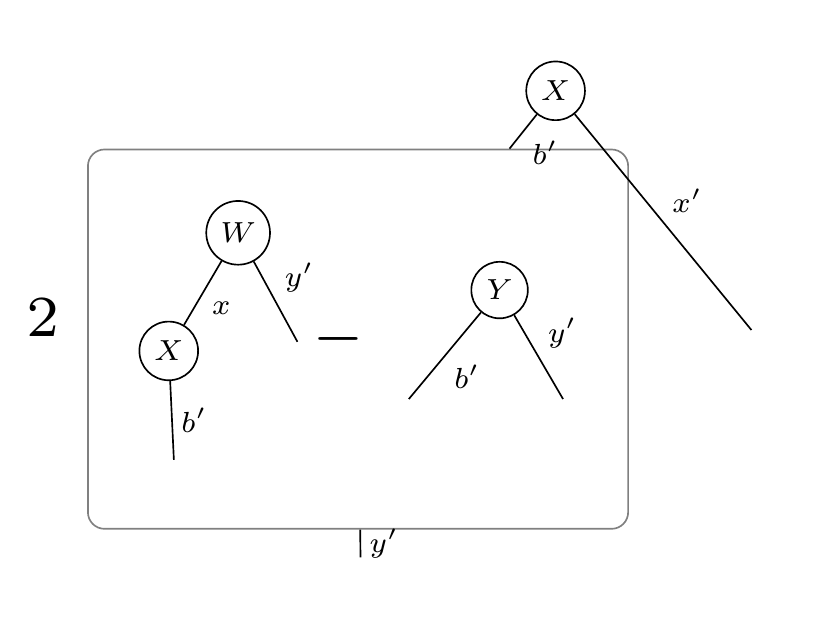
Step by Step Instructions

The neat thing about tensorgrad is that it will also give you the step by step instructions to see how the rules of derivatives are computed on tensors like this:

thomasahle / tensorgrad

readme