search

meyerls / pc-skeletor

Skeletonization of 3D Point Clouds
MIT License
153 stars 18 forks source link
3d-skeleton laplacian lbc pointcloud python s-lbc skeleton-extraction skeletonization

readme

PC Skeletor - Point Cloud Skeletonization

PyPI PyPI - Python Version license

PC Skeletor is a Python library for extracting a curved skeleton from 3d point clouds using Laplacian-Based Contraction and Semantic Laplacian-Based Contraction.

Abstract

Basic Laplacian-based contraction (LBC) is prone to mal-contraction in cases where there is a significant disparity in diameter between trunk and branches. In such cases fine structures experience an over-contraction and leading to a distortion of their topological characteristics. In addition, LBC shows a topologically incorrect tree skeleton for trunk structures that have holes in the point cloud.In order to address these topological artifacts, we introduce semantic Laplacian-based contraction (S-LBC). It integrates semantic information of the point cloud into the contraction algorithm to overcome these artifacts.

Laplacian-Based Contraction (LBC)

Image 1

Semantic LBC (S-LBC)

Image 2

⚡️ Quick Start

Installation

First install Python Version 3.8 or higher. The python package can be installed via PyPi using pip.

pip install pc-skeletor

Installation from Source

git clone https://github.com/meyerls/pc-skeletor.git
cd pc-skeletor
pip install --upgrade pip setuptools
pip install -r requirements.txt
pip install -e .

Basic Usage

The following code performs the skeletonization algorithm on a downloaded point cloud example. It also generates an animation that includes the original point cloud and the resulting skeleton, which is exported as a gif.

Download Example Dataset

import open3d as o3d
import numpy as np

from pc_skeletor import Dataset

downloader = Dataset()
trunk_pcd_path, branch_pcd_path = downloader.download_semantic_tree_dataset()

pcd_trunk = o3d.io.read_point_cloud(trunk_pcd_path)
pcd_branch = o3d.io.read_point_cloud(branch_pcd_path)
pcd = pcd_trunk + pcd_branch

Laplacian-Based Contraction (LBC)

from pc_skeletor import LBC

lbc = LBC(point_cloud=pcd,
          down_sample=0.008)
lbc.extract_skeleton()
lbc.extract_topology()

# Debug/Visualization
lbc.visualize()
lbc.export_results('./output')
lbc.animate(init_rot=np.asarray([[1, 0, 0], [0, 0, 1], [0, 1, 0]]),
            steps=300,
            output='./output')

Semantic Laplacian-Based Contraction (S-LBC)

from pc_skeletor import SLBC

s_lbc = SLBC(point_cloud={'trunk': pcd_trunk, 'branches': pcd_branch},
             semantic_weighting=30,
             down_sample=0.008,
             debug=True)
s_lbc.extract_skeleton()
s_lbc.extract_topology()

# Debug/Visualization
s_lbc.visualize()
s_lbc.show_graph(s_lbc.skeleton_graph)
s_lbc.show_graph(s_lbc.topology_graph)
s_lbc.export_results('./output')
s_lbc.animate(init_rot=np.asarray([[1, 0, 0], [0, 0, 1], [0, 1, 0]]), steps=300, output='./output')

Output

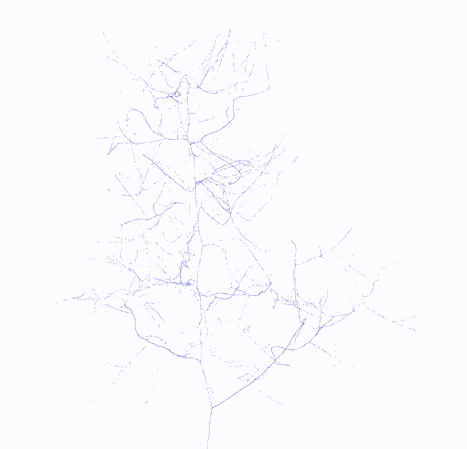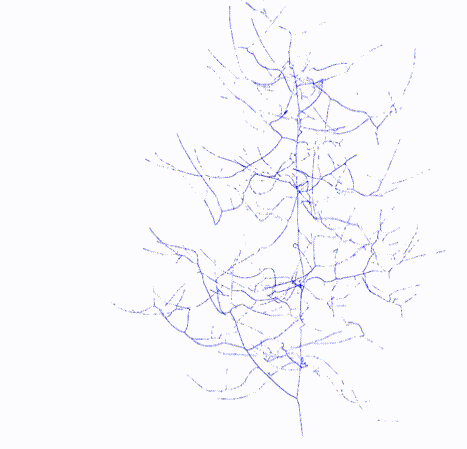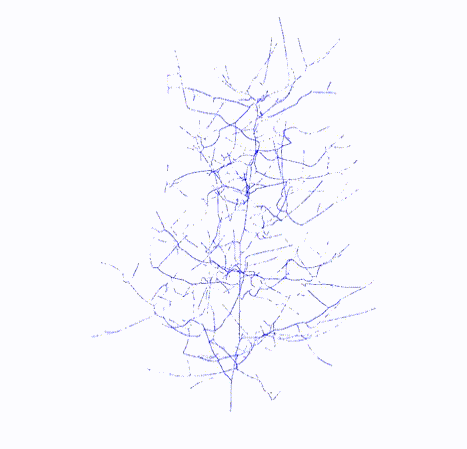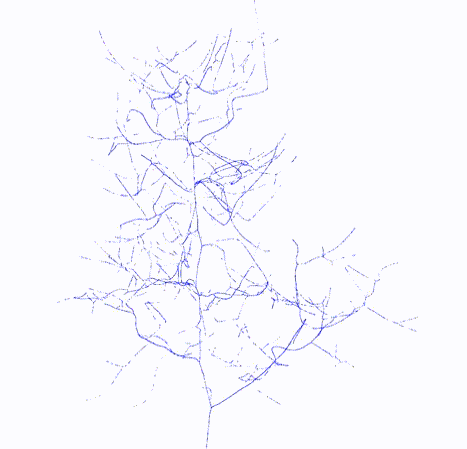
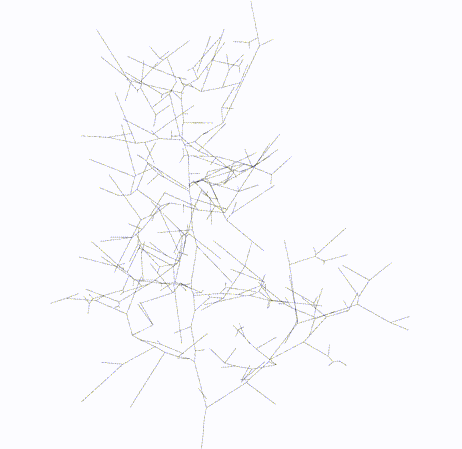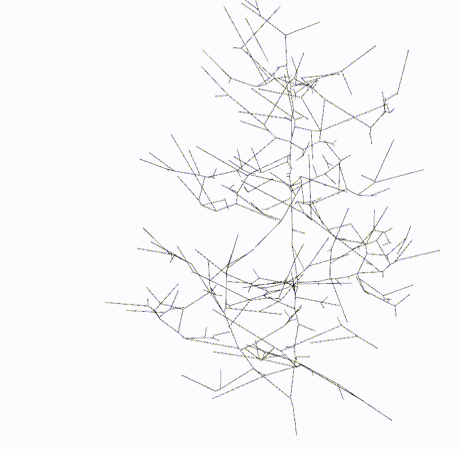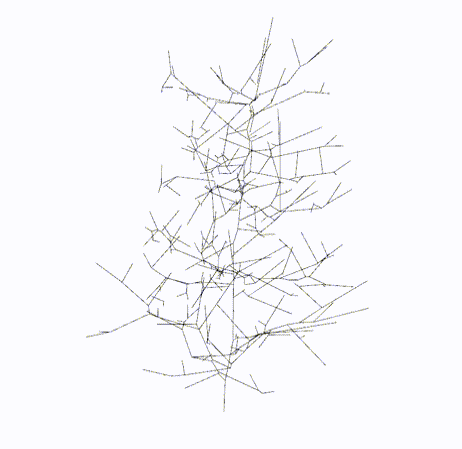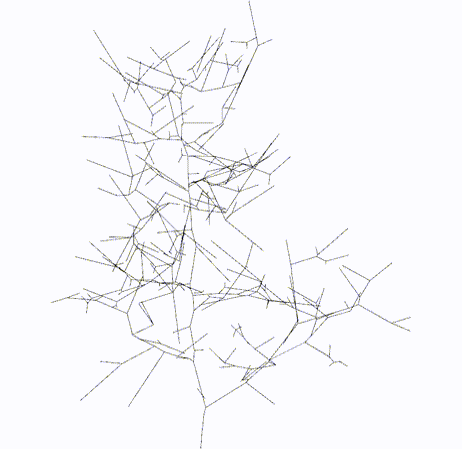
Skeleton Topology Skeletal Graph Topology Graph 
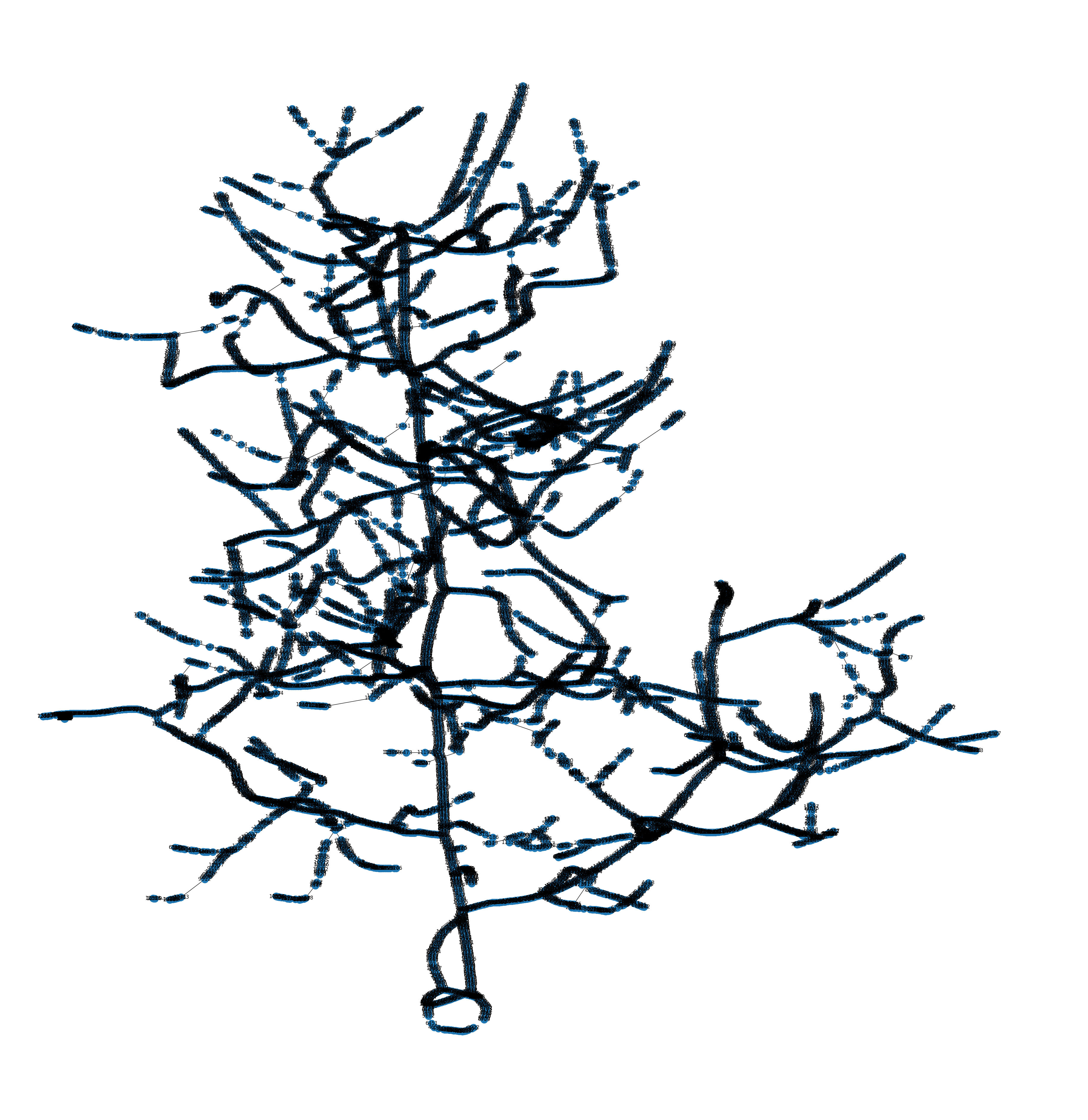
lbc.contracted_point_cloud: o3d.geometry.PointCloud
lbc.skeleton: o3d.geometry.PointCloud
lbc.skeleton_graph: networkx.nx
lbc.topology: o3d.geometry.LineSet
lbc.topology_graph: networkx.nx

Ω Parametrization

Laplacian-Based Contraction

Laplacian-Based Contraction is a method based on contraction of point clouds to extract curve skeletons by iteratively contracting the point cloud. This method is robust to missing data and noise. Additionally no prior knowledge on the topology of the object has to be made.

The contraction is computed by iteratively solving the linear system

\begin{bmatrix}
\mathbf{W_L} \mathbf{L}\\
\mathbf{W_H}
\end{bmatrix} \mathbf{P}^{'} =
\begin{bmatrix}
\mathbf{0}\\
\mathbf{W_H} \mathbf{P}
\end{bmatrix}

obtained from Kin-Chung Au et al. $\mathbf{L}$ is the $n \times n$ Laplacian Matrix with cotangent weights. The Laplacian of a point cloud (Laplace-Beltrami Operator) can be used to compute the mean curvature Vector(p. 88 & p. 100). $\mathbf{P}$ is the original point cloud, $\mathbf{P}^{'}$ a contracted point cloud and $\mathbf{W_L}$ and $\mathbf{W_H}$ are diagonal weight matrices balancing the contraction and attraction forces. During the contraction the point clouds get thinner and thinner until the solution converges. Afterwards the contracted point cloud aka. skeleton is sampled using farthest-point method.

To archive good contraction result and avoid over- and under-contraction it is necessary to initialize and update the weights $\mathbf{W_L}$ and $\mathbf{W_H}$. Therefore the initial values and the maximum values for both diagonal weighting matrices have to adjusted to archive good results.

Semantic Laplacian-Based Contraction

Semantic Laplacian-Based Contraction is based on Laplacian-based contraction and simply adds semantic knowledge to the skeletonization algorithm.

\begin{bmatrix}
\mathbf{S} \circ \mathbf{W_L} \mathbf{L}\\
\mathbf{W_H}
\end{bmatrix} \mathbf{P}^{'} =
\begin{bmatrix}
\mathbf{0}\\
\mathbf{W_H} \mathbf{P}
\end{bmatrix}

Standard LBC is prone to mal-contraction in cases where there is a significant disparity in diameter between trunk and branches. In such cases fine structures experience an over- contraction and leading to a distortion of their topological characteristics. In order to address these topological artifacts, we introduce semantic Laplacian-based contraction (S-LBC). For more information please refer to the [Paper].

📖 Literature and Code used for implementation

Laplacian based contraction

Our implementation of Point Cloud Skeletons via Laplacian-Based Contraction is a python reimplementation of the original Matlab code.

Robust Laplacian for Point Clouds

Computation of the discrete laplacian operator via Nonmanifold Laplace can be found in the robust-laplacians-py repository.

Minimum Spanning Tree

The Minimum Spanning Tree is computed via Mistree a open-source implementation which can be found here.

:interrobang: Troubleshooting

For Windows users, there might be issues installing the mistree library via python -m pip install mistree command. If you get an error message that the Fortran compiler cannot be found, please try the following:

:heavy_exclamation_mark: Limitation / Improvements

📖 Citation

Please cite this [Paper] if this work helps you with your research:

@misc{meyer2023cherrypicker,
      title={CherryPicker: Semantic Skeletonization and Topological Reconstruction of Cherry Trees}, 
      author={Lukas Meyer and Andreas Gilson and Oliver Scholz and Marc Stamminger},
      year={2023},
      eprint={2304.04708},
      archivePrefix={arXiv},
      primaryClass={cs.CV}
}