End-to-end Lane Detection
This repo contains the implementation of our paper End-to-end Lane Detection through Differentiable Least-Squares Fitting by Wouter Van Gansbeke, Bert De Brabandere, Davy Neven, Marc Proesmans and Luc Van Gool.
If you find this interesting or relevant for your work, consider citing:
@article{wvangansbeke_2019,
title={End-to-end Lane Detection through Differentiable Least-Squares Fitting},
author={Van Gansbeke, Wouter and De Brabandere, Bert and Neven, Davy and Proesmans, Marc and Van Gool, Luc},
journal={arXiv preprint arXiv:1902.00293},
year={2019}
}Update
I added a new directory __Backprojection_loss__ which is very similar to the other one. However, now the loss is a regression towards the coordinates in the original perspective instead of a regression in the birds eye view perspective towards the lane-line coefficients. We are primarily interested in the accuracy in this perspecitve after all. It also contains multi-lane detection experiments on the complete dataset of TuSimple (3626 images).
License
This software is released under a creative commons license which allows for personal and research use only. For a commercial license please contact the authors. You can view a license summary here.
Setup
This repository compares two methods to achieve higher accuracy for lane detection applications. The former is the conventional segmentation approach and the latter will tackle this problem in an end-to-end manner. The segmentation approach depends on the cross-entropy loss in order to learn the road markings by attention. However this approach is not necessarily the most accurate. Since the final line coordinates are desired, a complete end-to-end method should achieve better results.
This end-to-end architecture consist of two parts. The first part is an off the shelf network to predict weight maps. These weights are applied to a mesh grid which are used for the last step. The last step can be considered as the final layer of the network which solves a weighted system of equations to calculate the final curve parameters of the road markings. The amount of weight maps depends on the amount of lane lines the network ought to detect. This means that a direct regression can be performed to the desired curve coordinates. After all, backpropagation through the whole architecture is now possible.
Finally we show results for egolane detection. The implementation proofs that this direct optimization is indeed possible and can achieve better results than the conventional segmentation approach. Moreover, this module can be applied to a broad range of tasks since the first stage of the architecture can be chosen freely. The extention to other domains such as object detection is considered as future work which also shows the effectiveness of this architecture.
Requirements
I just updated the code to the most recent version of Pytorch (=pytorch 1.1) with python 3.7. The other required packages are: opencv, scikit-learn, torchvision, numpy, matplotlib, json/ujson and pillow.
Dataset
For the egolane detection experiment, I used a subset from the TuSimple dataset. You can download it here. You can find the images as well as the ground truth annotations in this folder to save you some work. Automatically 20% of the data will be used for validation. TuSimple provides the user 3 json files with ground truth coordinates of the lane lines. I appended the three files and used the index in this json file to name a specific image. For example: file "10.jpg" in the data directory corresponds with "10.png" in the ground truth directory and with index 10 in the json files (= label_data_all.json and Curve_parameters.json).
You can download the complete TuSimple dataset from here.
In the file Labels/Curve_parameters.json, the coefficients of the second degree polynomials are shown for the multiple lane lines in a bird's eye view perspective for the a subset of the data. (three zeros means that the lane line is not present in the image). So, the coefficients for the whole dataset are already computed for you.
Run Code
To run the code (training phase):
python main.py --image_dir /path/to/image/folder --gt_dir /path/to/ground_truth/folder --end_to_end True
Flags:
- Set flag "end_to_end" to True to regress towards the final lane line coefficients directly.
- See
python main.py --helpfor more information.
The weight maps will be computed but be aware that the appearance of the weight maps is architecture dependent. Augmenting this method with a line type branch in a shared encoder setup, results in:
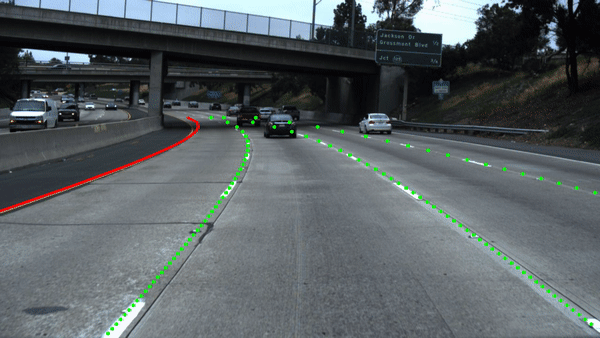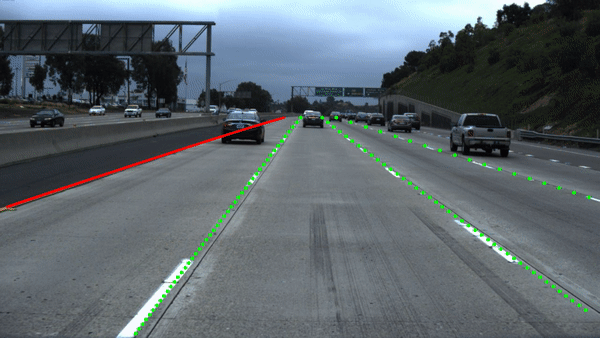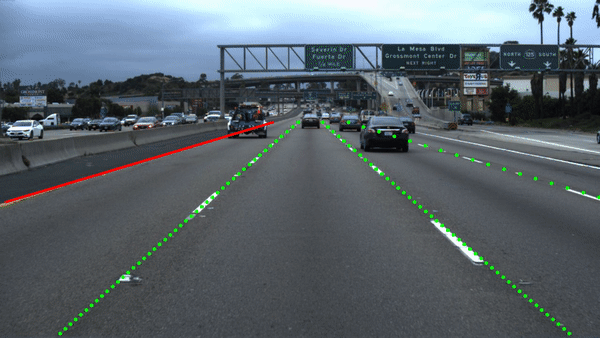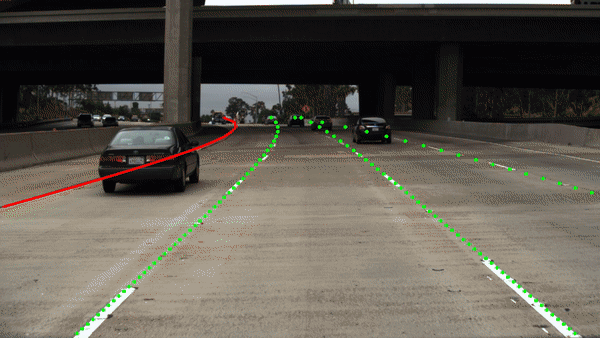
Results Egolane Detection
Our network architecture is based on ERFNet.
| Method | Model | Area metric | Area2 loss |
|---|---|---|---|
| Segmentation | ERFNet | 1.603e-3 normalized | 2.733e-5 normalized |
| End to end | ERFNet | 1.437e-3 normalized | 1.912e-5 normalized |
| Gain | ERFNet | 1.66e-4*(19.1mx38.2m)/21 = 0.06 m2 | 8.21e-6 normalized |
(1 Based on 3.7 m standard lane width in the US)
General Discussion
Practical discussion for multi lane detection:
-
Instance segmentation: We primarily want to focus on our differentiable least squares module from our paper. This module is compatible with whatever method you choose. See it as an extra layer of the network to make lane detection completely end-to-end. Hence, an instance segmentation method can be combined with our method.
-
To detect multiple lanes more robustly, the mask in the
Networks/LSQ_layer.pyfile can be exploited. -
Continual learning setup: A possibility is to focus first on egolanes and add more lane lines during training. This makes the task more difficult over time. This will improve the convergence, since the features of the first lane lines can help to detect the later ones.
-
Pretrainig: When a high number of lane lines are desired to be detected, the supervision could be be too weak (depending on the initialization and the network). Pretraining using a few segmentation labels is a good way to alleviate this problem.
-
Proxy segmentation task: You could also combine our method with a proxy segmentation task in a shared encoder architecture. This can have some benefits (i.e. good initialization for the weight maps), although this makes the setup more complex.
Results Discussion
Egolane setup:
In this case you only need to detect the line on the left and right of the car. It should be fairly easy to get the numbers reported in the paper with the provided code above.
Multi-lane setup:
We actually advise to use our proposed loss jointly with a cross-entropy loss on the segmentation maps (proxy task), since it is the most robust one. It forces the network to look at the lane-lines during training, stabilizing the training. The proposed least squares loss still improves over the vanilla cross-entropy loss, since it's able to optimize for the desired y-coordinates directly. By additionally finetuning the fixed birds-eye view transformation matrix you should get around 95.8%. If you don't use any additional attention nor finetuning, you should get around 93.2% on the TuSimple test set.
Acknowledgement
This work was supported by Toyota, and was carried out at the TRACE Lab at KU Leuven (Toyota Research on Automated Cars in Europe - Leuven)