VectorizedMultiAgentSimulator (VMAS)

[!NOTE]
We have released BenchMARL, a benchmarking library where you can train VMAS tasks using TorchRL! Check out how easy it is to use it.

Welcome to VMAS!

This repository contains the code for the Vectorized Multi-Agent Simulator (VMAS).

VMAS is a vectorized differentiable simulator designed for efficient MARL benchmarking. It is comprised of a fully-differentiable vectorized 2D physics engine written in PyTorch and a set of challenging multi-robot scenarios. Scenario creation is made simple and modular to incentivize contributions. VMAS simulates agents and landmarks of different shapes and supports rotations, elastic collisions, joints, and custom gravity. Holonomic motion models are used for the agents to simplify simulation. Custom sensors such as LIDARs are available and the simulator supports inter-agent communication. Vectorization in PyTorch allows VMAS to perform simulations in a batch, seamlessly scaling to tens of thousands of parallel environments on accelerated hardware. VMAS has an interface compatible with OpenAI Gym, with Gymnasium, with RLlib, with torchrl and its MARL training library: BenchMARL, enabling out-of-the-box integration with a wide range of RL algorithms. The implementation is inspired by OpenAI's MPE. Alongside VMAS's scenarios, we port and vectorize all the scenarios in MPE.

Paper

The arXiv paper can be found here.

If you use VMAS in your research, cite it using:

@article{bettini2022vmas,
  title = {VMAS: A Vectorized Multi-Agent Simulator for Collective Robot Learning},
  author = {Bettini, Matteo and Kortvelesy, Ryan and Blumenkamp, Jan and Prorok, Amanda},
  year = {2022},
  journal={The 16th International Symposium on Distributed Autonomous Robotic Systems},
  publisher={Springer}
}

Video

Watch the presentation video of VMAS, showing its structure, scenarios, and experiments.

[](https://www.youtube.com/watch?v=aaDRYfiesAY)

Watch the talk at DARS 2022 about VMAS.

[](https://www.youtube.com/watch?v=boViBY7Woqg)

Table of contents

• VectorizedMultiAgentSimulator (VMAS)
  • Welcome to VMAS!
  • Paper
  • Video
  • Table of contents
  • How to use
  • Notebooks
  • Install
  • Run
    • RLlib
    • TorchRL
  • Input and output spaces
    • Output spaces
    • Input action space
  • Simulator features
  • Creating a new scenario
  • Play a scenario
  • Rendering
  • Plot function under rendering
  • Rendering on server machines
  • List of environments
  • VMAS
    • Main scenarios
    • Debug scenarios
  • MPE
  • Our papers using VMAS
  • TODOS

How to use

Notebooks

•   Using a VMAS environment. Here is a simple notebook that you can run to create, step and render any scenario in VMAS. It reproduces the use_vmas_env.py script in the examples folder.
•   Training VMAS in BenchMARL (suggested). In this notebook, we show how to use VMAS in BenchMARL, TorchRL's MARL training library.
•   Training VMAS in TorchRL. In this notebook, available in the TorchRL docs, we show how to use any VMAS scenario in TorchRL. It will guide you through the full pipeline needed to train agents using MAPPO/IPPO.
•   Training competitive VMAS MPE in TorchRL. In this notebook, available in the TorchRL docs, we show how to solve a Competitive Multi-Agent Reinforcement Learning (MARL) problem using MADDPG/IDDPG.
•   Training VMAS in RLlib. In this notebook, we show how to use any VMAS scenario in RLlib. It reproduces the rllib.py script in the examples folder.

Install

To install the simulator, you can use pip to get the latest release:

pip install vmas

If you want to install the current master version (more up to date than latest release), you can do:

git clone https://github.com/proroklab/VectorizedMultiAgentSimulator.git
cd VectorizedMultiAgentSimulator
pip install -e .

By default, vmas has only the core requirements. To install further dependencies to enable training with Gymnasium wrappers, RLLib wrappers, for rendering, and testing, you may want to install these further options:

# install gymnasium for gymnasium wrappers
pip install vmas[gymnasium]

# install rllib for rllib wrapper
pip install vmas[rllib]

# install rendering dependencies
pip install vmas[render]

# install testing dependencies
pip install vmas[test]

# install all dependencies
pip install vmas[all]

You can also install the following training libraries:

pip install benchmarl # For training in BenchMARL
pip install torchrl # For training in TorchRL
pip install "ray[rllib]"==2.1.0 # For training in RLlib. We support versions "ray[rllib]<=2.2,>=1.13"

Run

To use the simulator, simply create an environment by passing the name of the scenario you want (from the scenarios folder) to the make_env function. The function arguments are explained in the documentation. The function returns an environment object with the VMAS interface:

Here is an example:

 env = vmas.make_env(
        scenario="waterfall", # can be scenario name or BaseScenario class
        num_envs=32,
        device="cpu", # Or "cuda" for GPU
        continuous_actions=True,
        wrapper=None,  # One of: None, "rllib", "gym", "gymnasium", "gymnasium_vec"
        max_steps=None, # Defines the horizon. None is infinite horizon.
        seed=None, # Seed of the environment
        dict_spaces=False, # By default tuple spaces are used with each element in the tuple being an agent.
        # If dict_spaces=True, the spaces will become Dict with each key being the agent's name
        grad_enabled=False, # If grad_enabled the simulator is differentiable and gradients can flow from output to input
        terminated_truncated=False, # If terminated_truncated the simulator will return separate `terminated` and `truncated` flags in the `done()`, `step()`, and `get_from_scenario()` functions instead of a single `done` flag
        **kwargs # Additional arguments you want to pass to the scenario initialization
    )

A further example that you can run is contained in use_vmas_env.py in the examples directory.

With the terminated_truncated flag set to True, the simulator will return separate terminated and truncated flags in the done(), step(), and get_from_scenario() functions instead of a single done flag. This is useful when you want to know if the environment is done because the episode has ended or because the maximum episode length/ timestep horizon has been reached. See the Gymnasium documentation for more details on this.

RLlib

To see how to use VMAS in RLlib, check out the script in examples/rllib.py.

You can find more examples of multi-agent training in VMAS in the HetGPPO repository.

TorchRL

VMAS is supported by TorchRL and its MARL training library BenchMARL.

Check out how simple it is to use VMAS in BenchMARL with this notebook.

We provide a notebook which guides you through a full multi-agent reinforcement learning pipeline for training VMAS scenarios in TorchRL using MAPPO/IPPO.

You can find example scripts in the TorchRL repo here on how to run MAPPO-IPPO-MADDPG-QMIX-VDN using the VMAS wrapper.

Input and output spaces

VMAS uses gym spaces for input and output spaces. By default, action and observation spaces are tuples:

spaces.Tuple(
    [agent_space for agent in agents]
)

When creating the environment, by setting dict_spaces=True, tuples can be changed to dictionaries:

spaces.Dict(
  {agent.name: agent_space for agent in agents}
)

Output spaces

If dict_spaces=False, observations, infos, and rewards returned by the environment will be a list with each element being the value for that agent.

If dict_spaces=True, observations, infos, and rewards returned by the environment will be a dictionary with each element having key = agent_name and value being the value for that agent.

Each agent observation in either of these structures is either (depending on how you implement the scenario):

• a tensor with shape [num_envs, observation_size], where observation_size is the size of the agent's observation.

  def observation(self, agent: Agent):
      return torch.cat([agent.state.pos, agent.state.vel], dim=-1)

• a dictionary of such tensors

  def observation(self, agent: Agent):
      return {
          "pos": agent.state.pos,
          "nested": {"vel": agent.state.vel},
      }

Each agent reward in either of these structures is a tensor with shape [num_envs].

Each agent info in either of these structures is a dictionary where each entry has key representing the name of that info and value a tensor with shape [num_envs, info_size], where info_size is the size of that info for that agent.

Done is a tensor of shape [num_envs].

Input action space

Each agent in vmas has to provide an action tensor with shape [num_envs, action_size], where num_envs is the number of vectorized environments and action_size is the size of the agent's action.

The agents' actions can be provided to the env.step() in two ways:

• A List of length equal to the number of agents which looks like [tensor_action_agent_0, ..., tensor_action_agent_n]
• A Dict of length equal to the number of agents and with each entry looking like {agent_0.name: tensor_action_agent_0, ..., agent_n.name: tensor_action_agent_n}

Users can interchangeably use either of the two formats and even change formats during execution, vmas will always perform all sanity checks. Each format will work regardless of the fact that tuples or dictionary spaces have been chosen.

Simulator features

• Vectorized: VMAS vectorization can step any number of environments in parallel. This significantly reduces the time needed to collect rollouts for training in MARL.
• Simple: Complex vectorized physics engines exist (e.g., Brax), but they do not scale efficiently when dealing with multiple agents. This defeats the computational speed goal set by vectorization. VMAS uses a simple custom 2D dynamics engine written in PyTorch to provide fast simulation.
• General: The core of VMAS is structured so that it can be used to implement general high-level multi-robot problems in 2D. It can support adversarial as well as cooperative scenarios. Holonomic point-robot simulation has been chosen to focus on general high-level problems, without learning low-level custom robot controls through MARL.
• Extensible: VMAS is not just a simulator with a set of environments. It is a framework that can be used to create new multi-agent scenarios in a format that is usable by the whole MARL community. For this purpose, we have modularized the process of creating a task and introduced interactive rendering to debug it. You can define your own scenario in minutes. Have a look at the dedicated section in this document.
• Compatible: VMAS has wrappers for RLlib, torchrl, OpenAI Gym and Gymnasium. RLlib and torchrl have a large number of already implemented RL algorithms. Keep in mind that this interface is less efficient than the unwrapped version. For an example of wrapping, see the main of make_env.
• Tested: Our scenarios come with tests which run a custom designed heuristic on each scenario.
• Entity shapes: Our entities (agent and landmarks) can have different customizable shapes (spheres, boxes, lines). All these shapes are supported for elastic collisions.
• Faster than physics engines: Our simulator is extremely lightweight, using only tensor operations. It is perfect for running MARL training at scale with multi-agent collisions and interactions.
• Customizable: When creating a new scenario of your own, the world, agent and landmarks are highly customizable. Examples are: drag, friction, gravity, simulation timestep, non-differentiable communication, agent sensors (e.g. LIDAR), and masses.
• Non-differentiable communication: Scenarios can require agents to perform discrete or continuous communication actions.
• Gravity: VMAS supports customizable gravity.
• Sensors: Our simulator implements ray casting, which can be used to simulate a wide range of distance-based sensors that can be added to agents. We currently support LIDARs. To see available sensors, have a look at the sensors script.
• Joints: Our simulator supports joints. Joints are constraints that keep entities at a specified distance. The user can specify the anchor points on the two objects, the distance (including 0), the thickness of the joint, if the joint is allowed to rotate at either anchor point, and if he wants the joint to be collidable. Have a look at the waterfall scenario to see how you can use joints. See the waterfall and joint_passage scenarios for an example.
• Agent actions: Agents' physical actions are 2D forces for holonomic motion. Agent rotation can also be controlled through a torque action (activated by setting agent.action.u_rot_range at agent creation time). Agents can also be equipped with continuous or discrete communication actions.
• Action preprocessing: By implementing the process_action function of a scenario, you can modify the agents' actions before they are passed to the simulator. This is used in controllers (where we provide different types of controllers to use) and dynamics (where we provide custom robot dynamic models).
• Controllers: Controllers are components that can be appended to the neural network policy or replace it completely. We provide a VelocityController which can be used to treat input actions as velocities (instead of default vmas input forces). This PID controller takes velocities and outputs the forces which are fed to the simulator. See the vel_control debug scenario for an example.
• Dynamic models: VMAS simulates holonomic dynamics models by default. Custom dynamics can be chosen at agent creation time. Implementations now include DiffDriveDynamics for differential drive robots, KinematicBicycleDynamics for kinematic bicycle model, and Drone for quadcopter dynamics. See diff_drive, kinematic_bicycle and drone debug scenarios for examples.
• Differentiable: By setting grad_enabled=True when creating an environment, the simulator will be differentiable, allowing gradients flowing through any of its function.

Creating a new scenario

To create a new scenario, just extend the BaseScenario class in scenario.py.

You will need to implement at least make_world, reset_world_at, observation, and reward. Optionally, you can also implement done, info, process_action, and extra_render.

You can also change the viewer size, zoom, and enable a background rendered grid by changing these inherited attributes in the make_world function.

To know how, just read the documentation of BaseScenario in scenario.py and look at the implemented scenarios.

Play a scenario

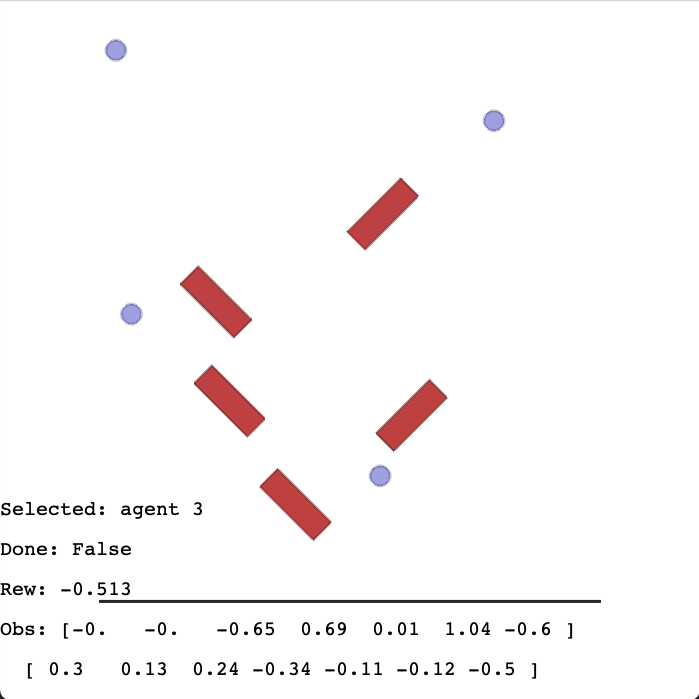
You can play with a scenario interactively! Just execute its script!

Just use the render_interactively function in the interactive_rendering.py script. Relevant values will be plotted to screen. Move the agent with the arrow keys and switch agents with TAB. You can reset the environment by pressing R. If you have more than 1 agent, you can control another one with W,A,S,D and switch the second agent using LSHIFT. To do this, just set control_two_agents=True. If the agents also have rotational actions, you can control them with M,N for the first agent and with Q,E (for example in the diff_drive scenario).

On the screen you will see some data from the agent controlled with arrow keys. This data includes: name, current obs, current reward, total reward so far and environment done flag.

Here is an overview of what it looks like:

Rendering

To render the environment, just call the render or the try_render_at functions (depending on environment wrapping).

Example:

env.render(
    mode="rgb_array", # "rgb_array" returns image, "human" renders in display
    agent_index_focus=4, # If None keep all agents in camera, else focus camera on specific agent
    index=0, # Index of batched environment to render
    visualize_when_rgb: bool = False, # Also run human visualization when mode=="rgb_array"
)

You can also change the viewer size, zoom, and enable a background rendered grid by changing these inherited attributes in the scenario make_world function.

Gif	Agent focus
	With agent_index_focus=None the camera keeps focus on all agents
	With agent_index_focus=0 the camera follows agent 0
	With agent_index_focus=4 the camera follows agent 4

Plot function under rendering

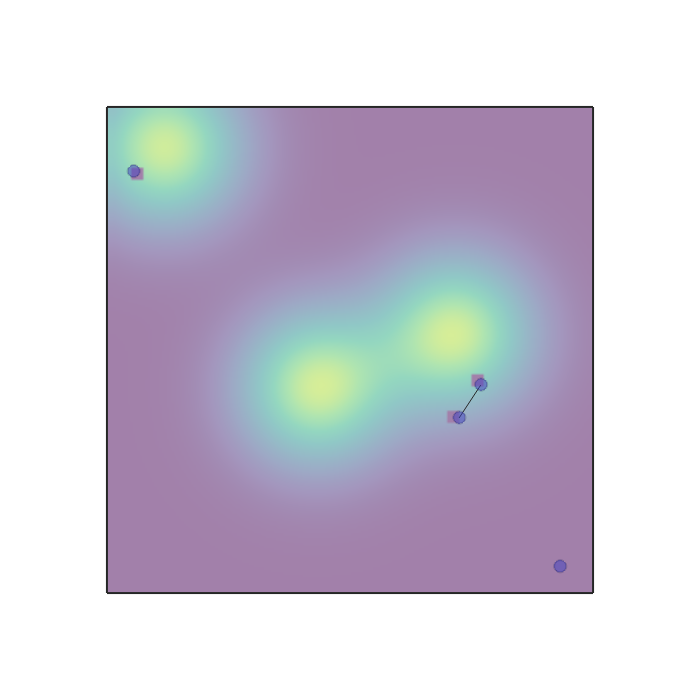
It is possible to plot a function under the rendering of the agents by providing a function f to the render function.

env.render(
    plot_position_function=f
)

The function takes a numpy array with shape (n_points, 2), which represents a set of x, y values to evaluate f over for plotting. f outputs either an array with shape (n_points, 1), which will be plotted as a colormap, or an array with shape (n_points, 4), which will be plotted as RGBA values.

See the sampling.py scenario for more info.

Rendering on server machines

To render in machines without a display use mode="rgb_array". Make sure you have OpenGL and Pyglet installed. To use GPUs for headless rendering, you can install the EGL library. If you do not have EGL, you need to create a fake screen. You can do this by running these commands before the script:

export DISPLAY=':99.0'
Xvfb :99 -screen 0 1400x900x24 > /dev/null 2>&1 &

or in this way:

xvfb-run -s \"-screen 0 1400x900x24\" python <your_script.py>

To create a fake screen you need to have Xvfb installed.

List of environments

VMAS

dropout	football	transport
wheel	balance	reverse transport
give_way	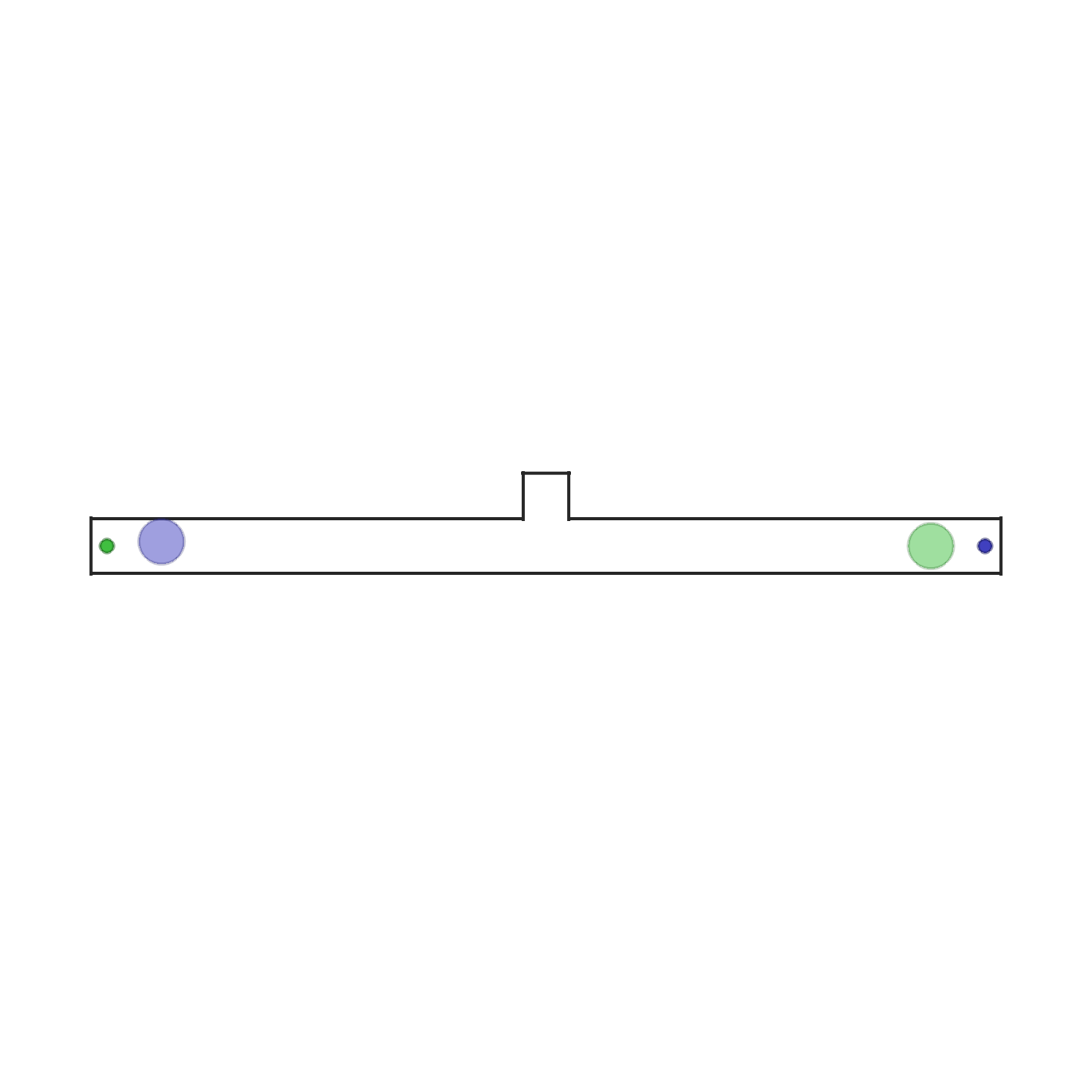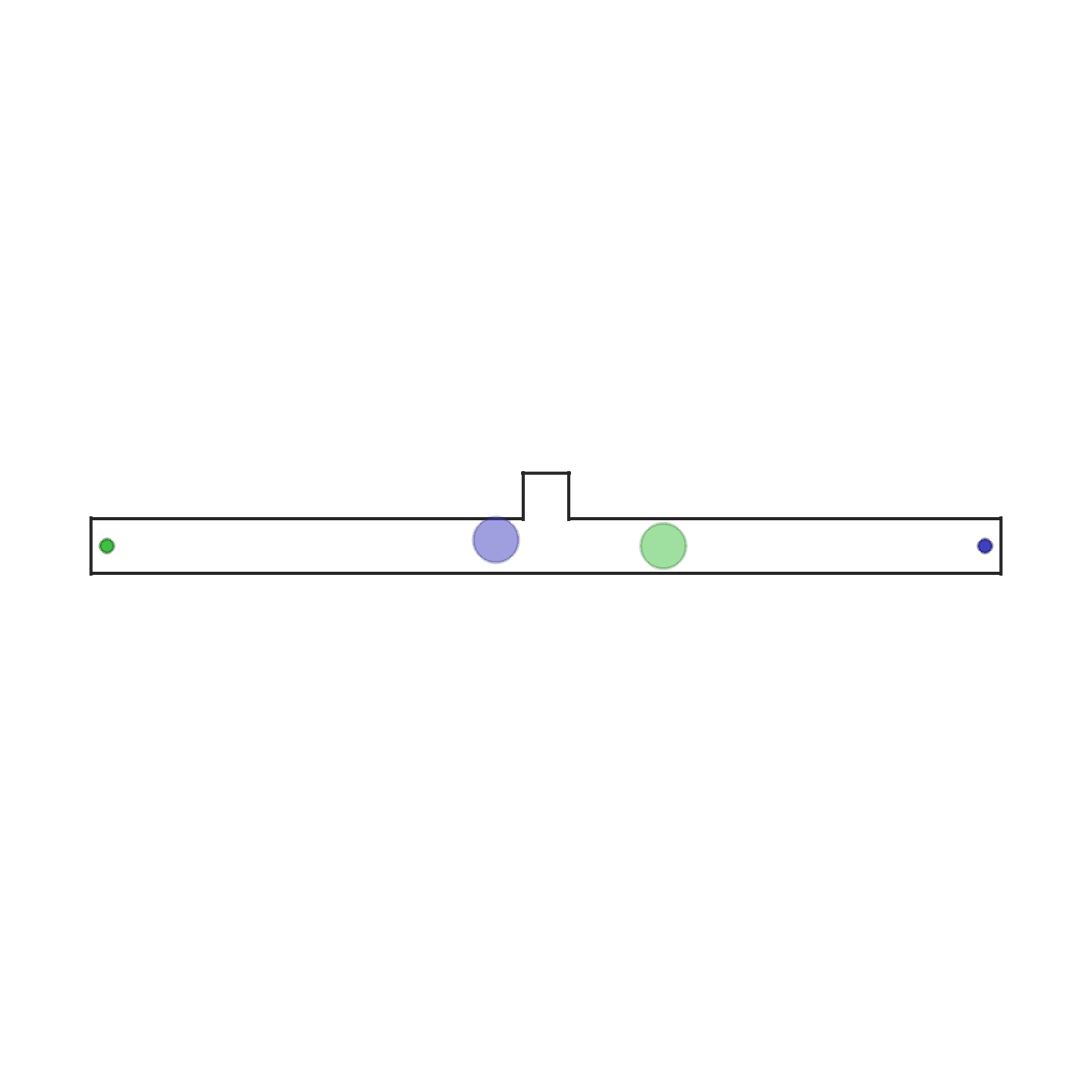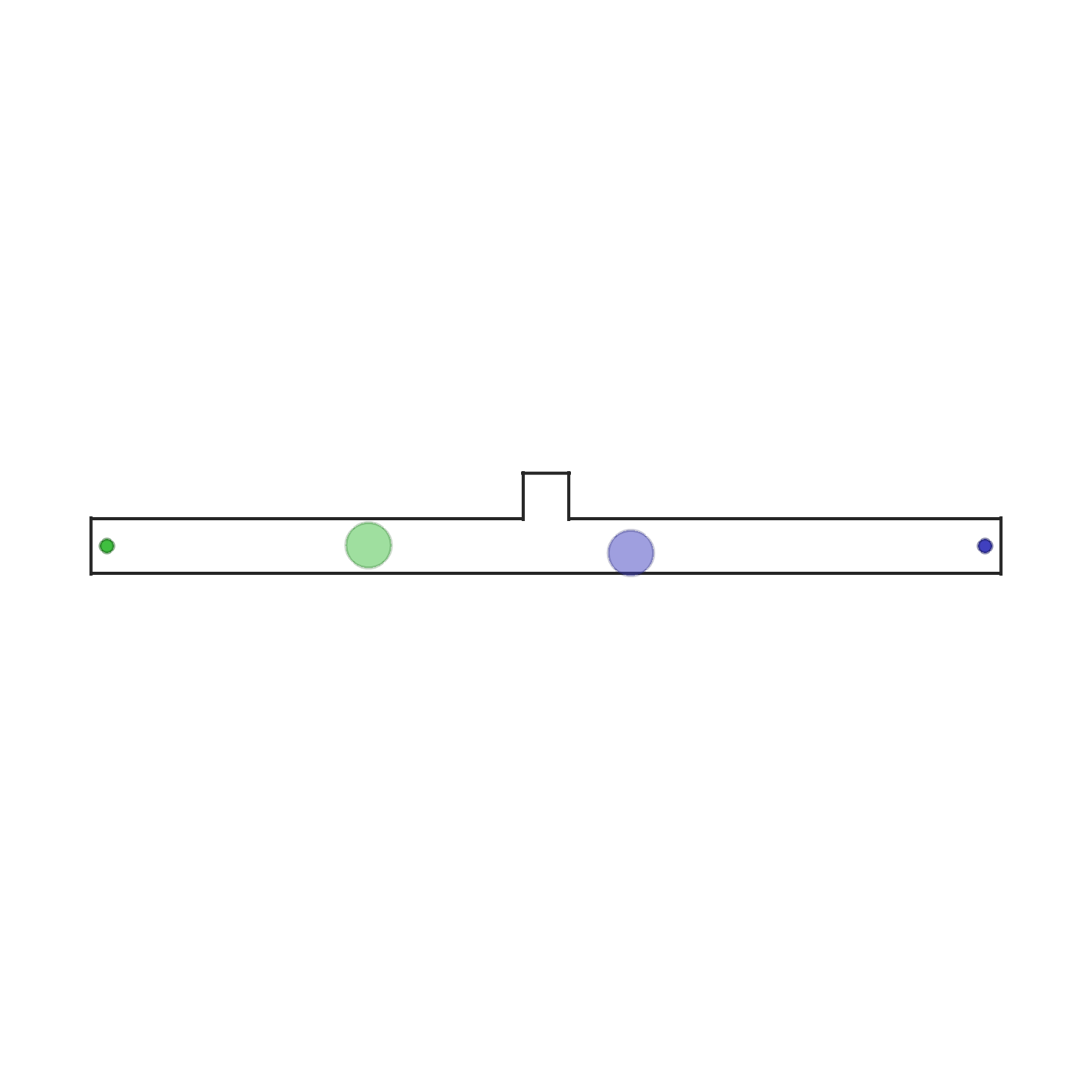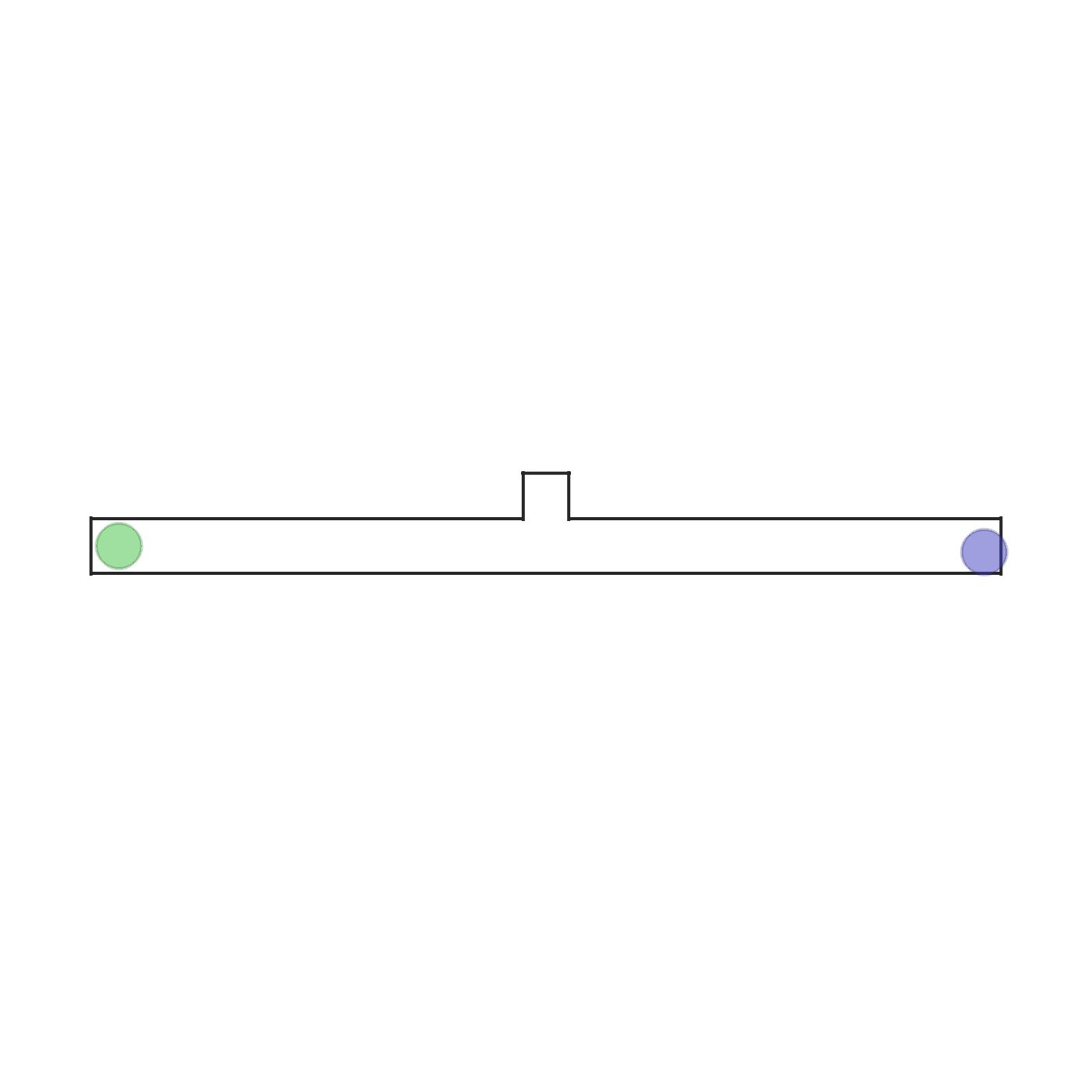passage	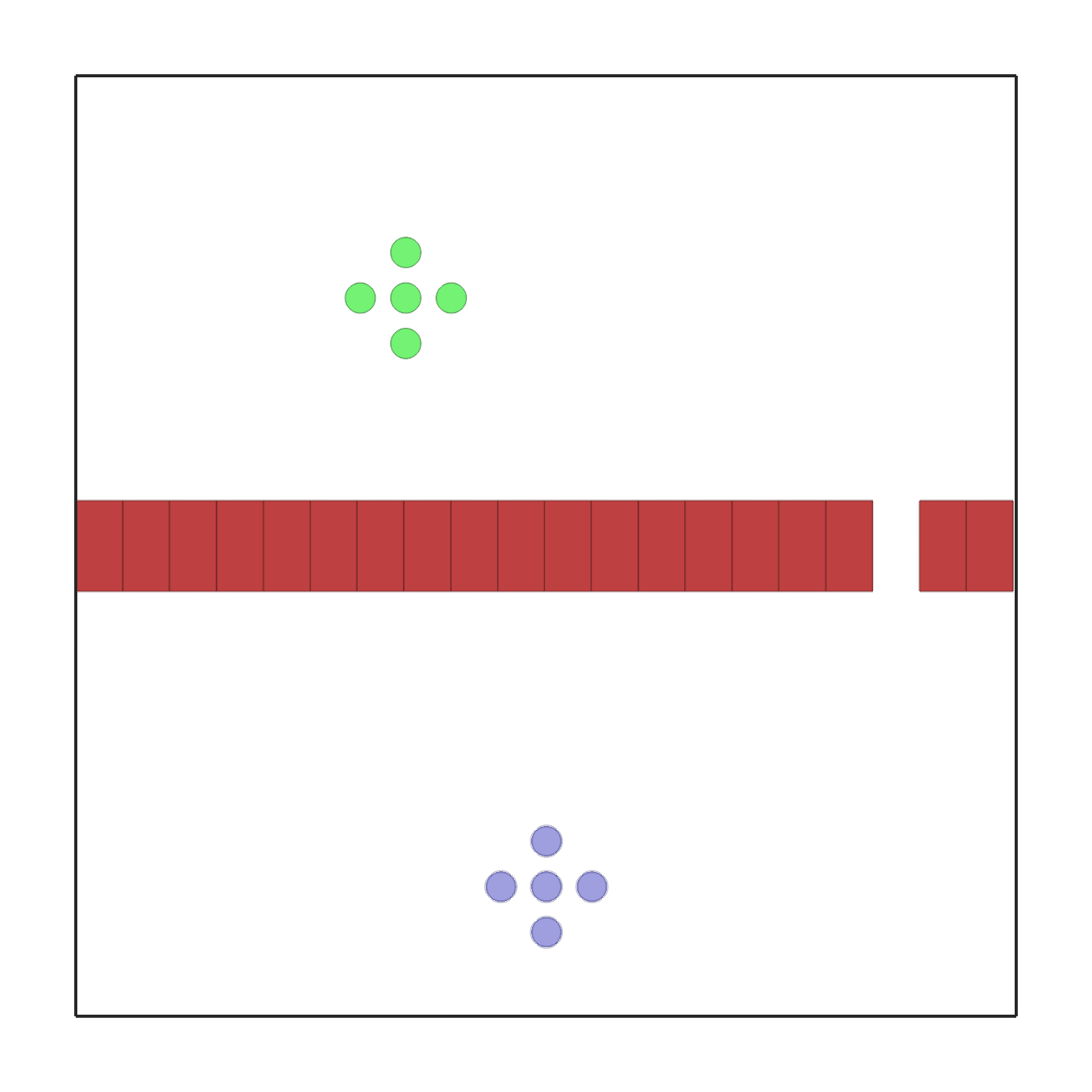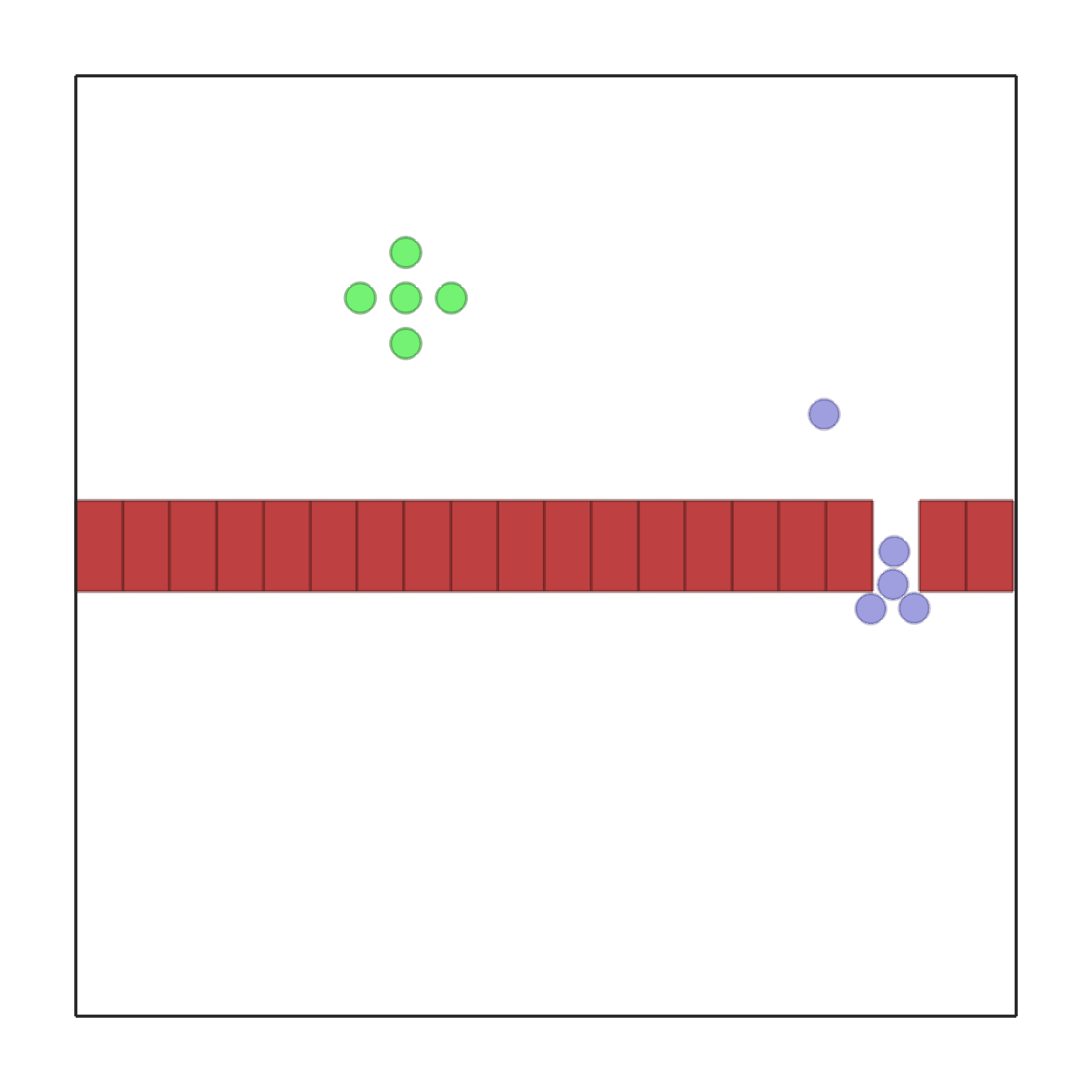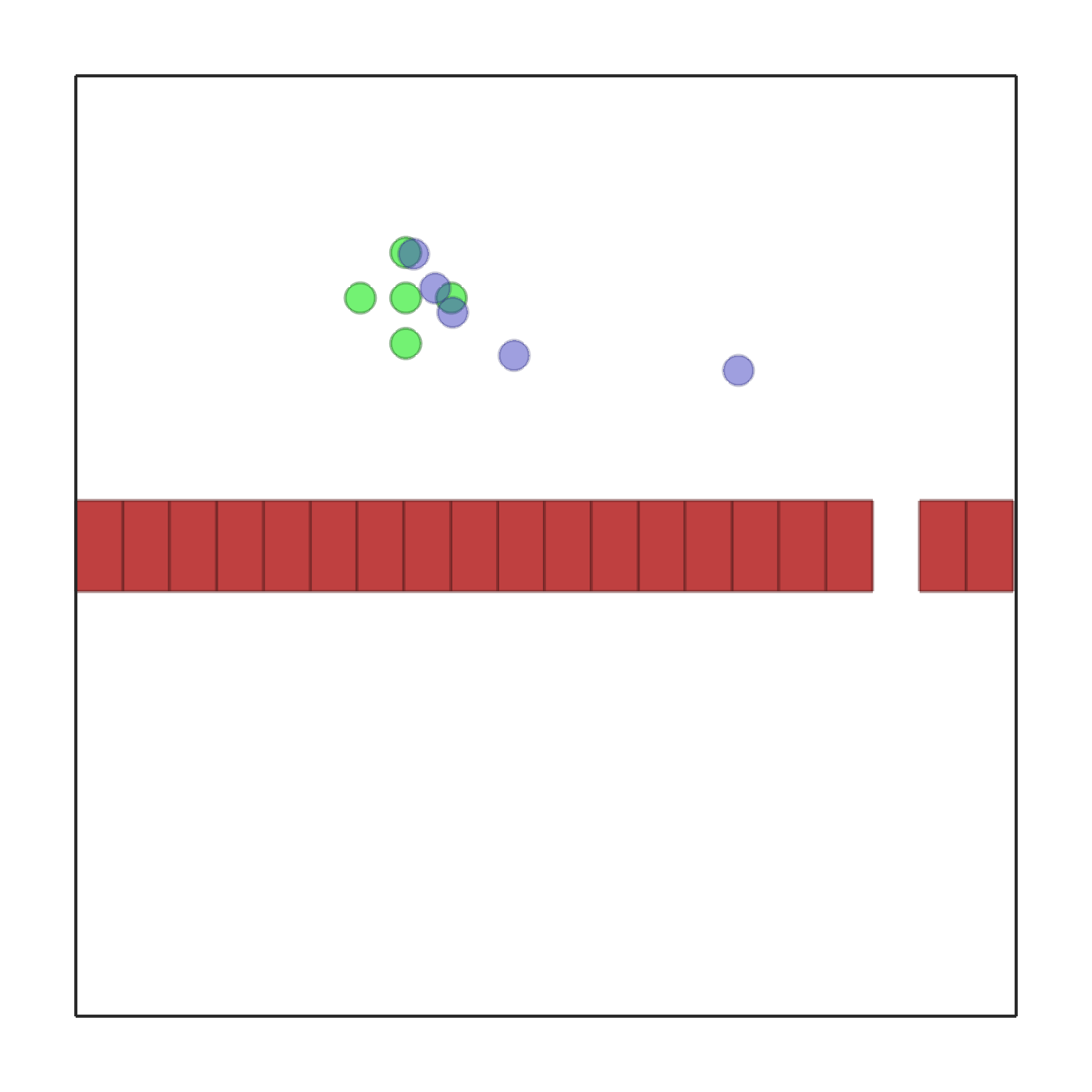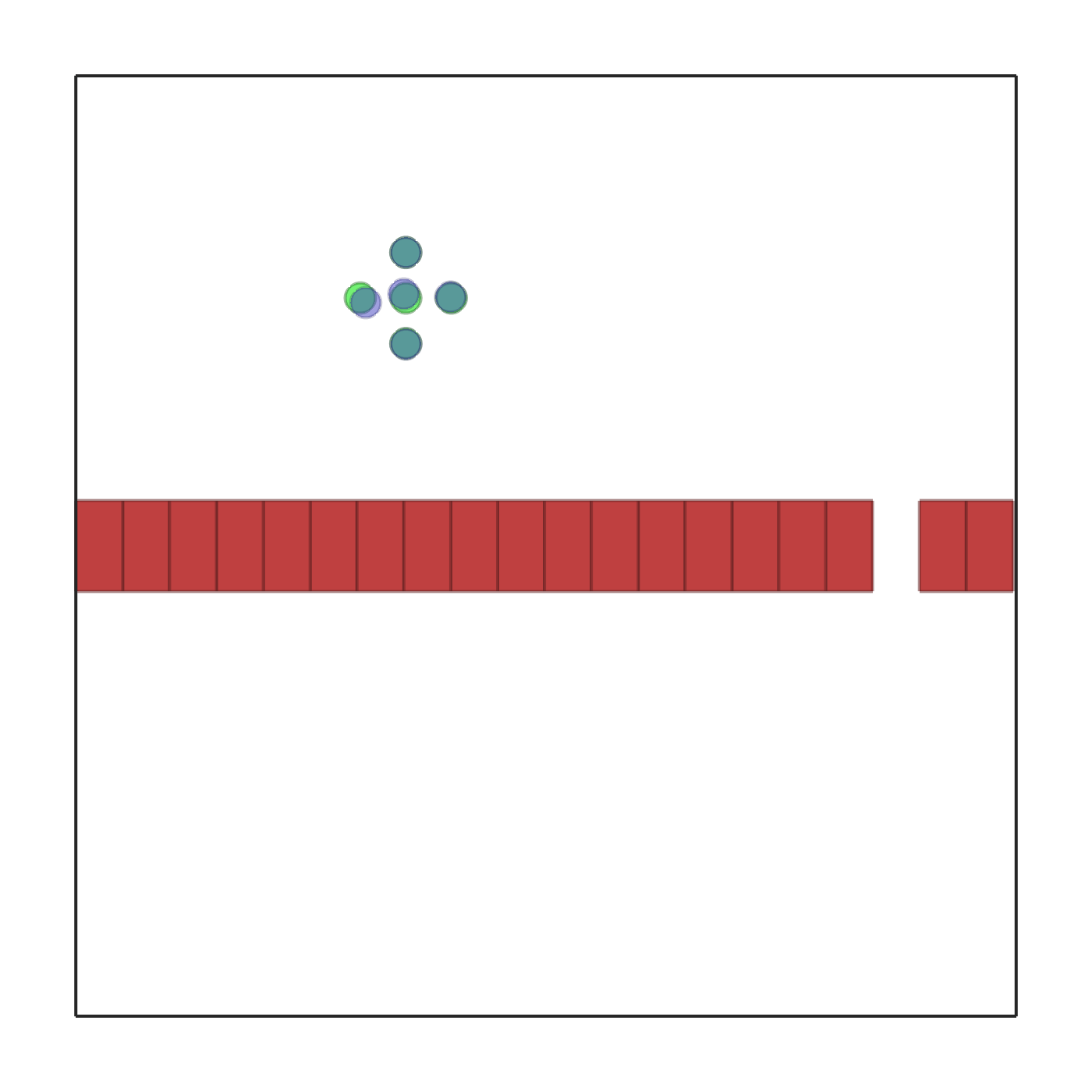dispersion
joint_passage_size	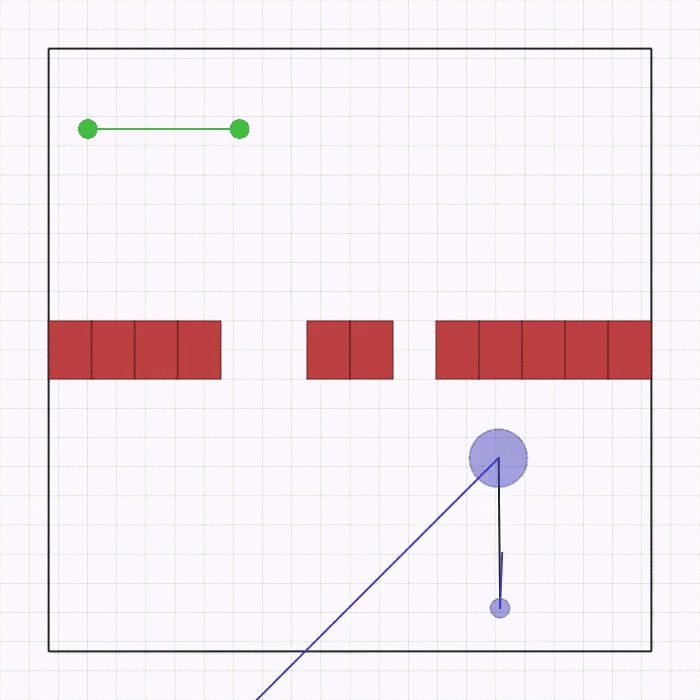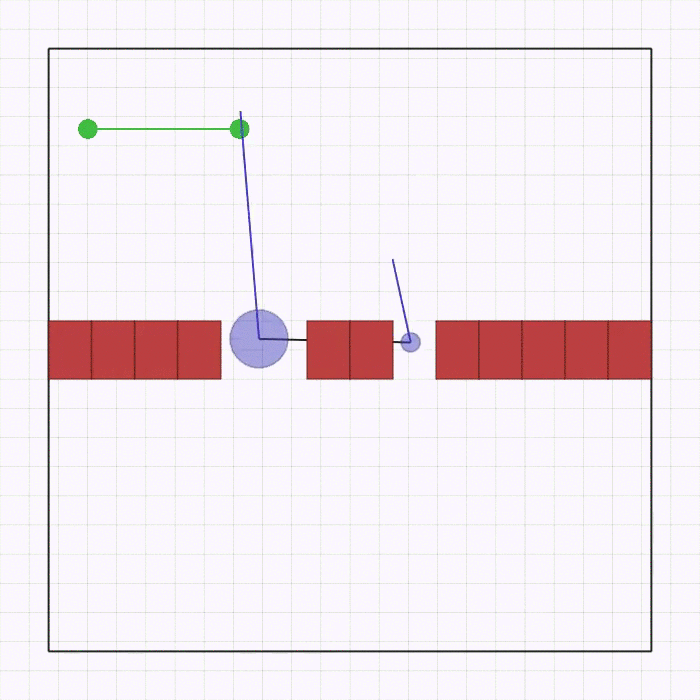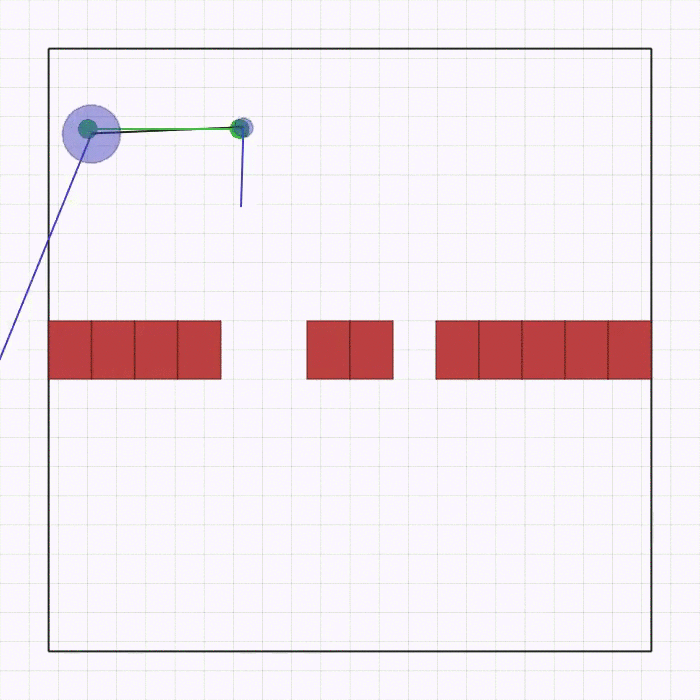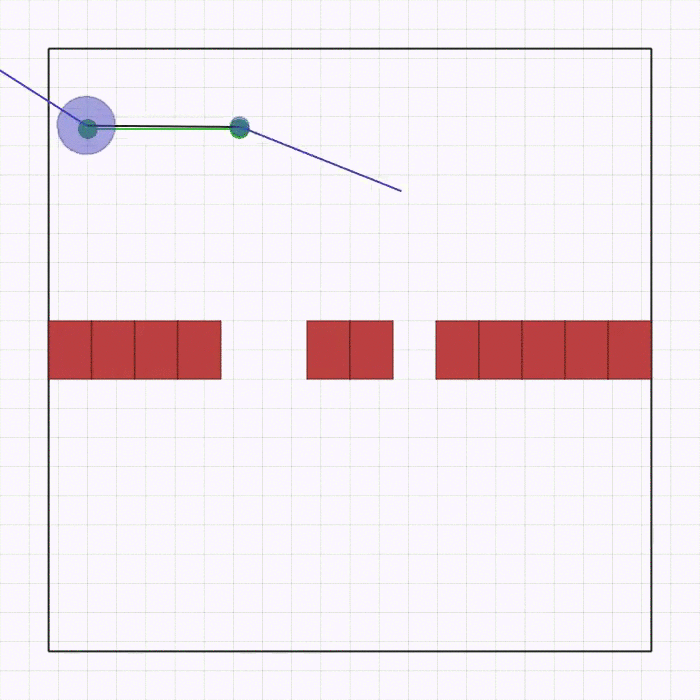flocking	discovery
joint_passage	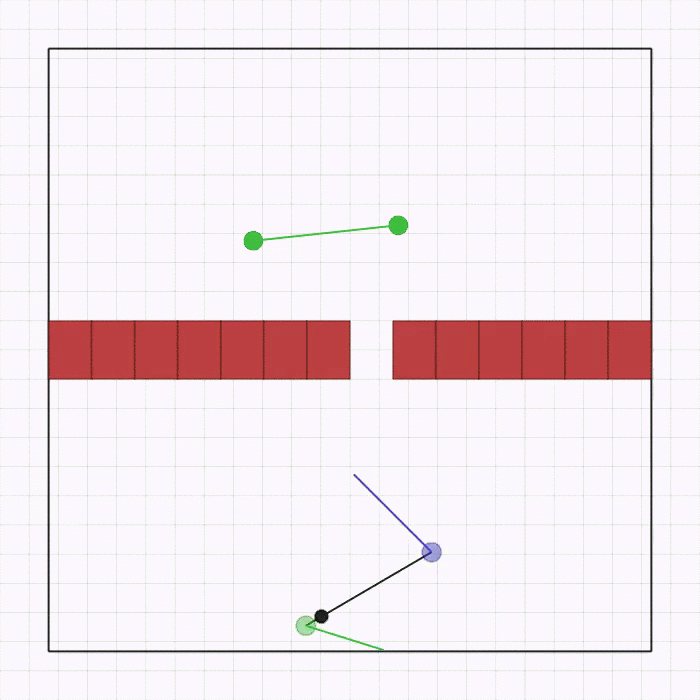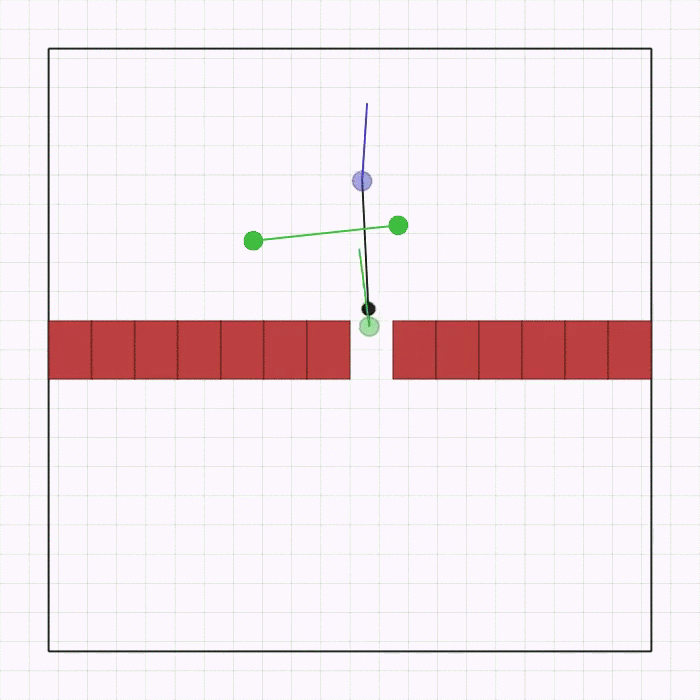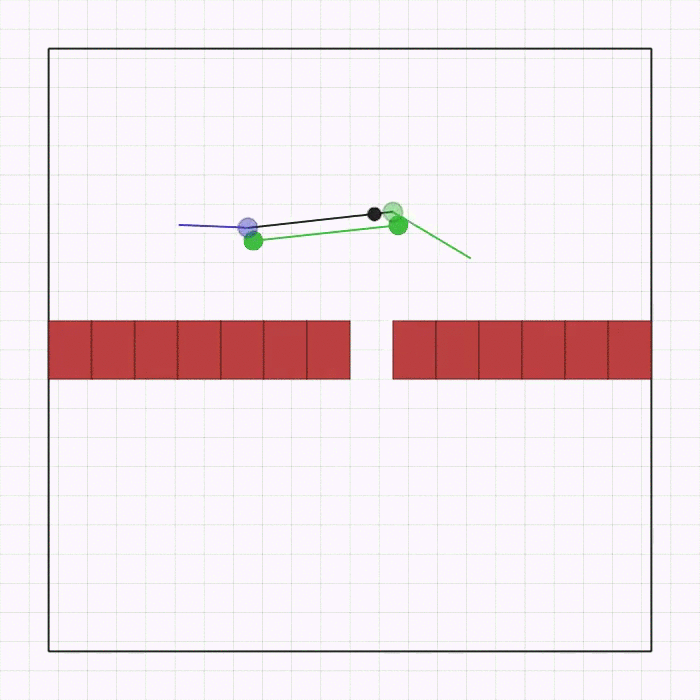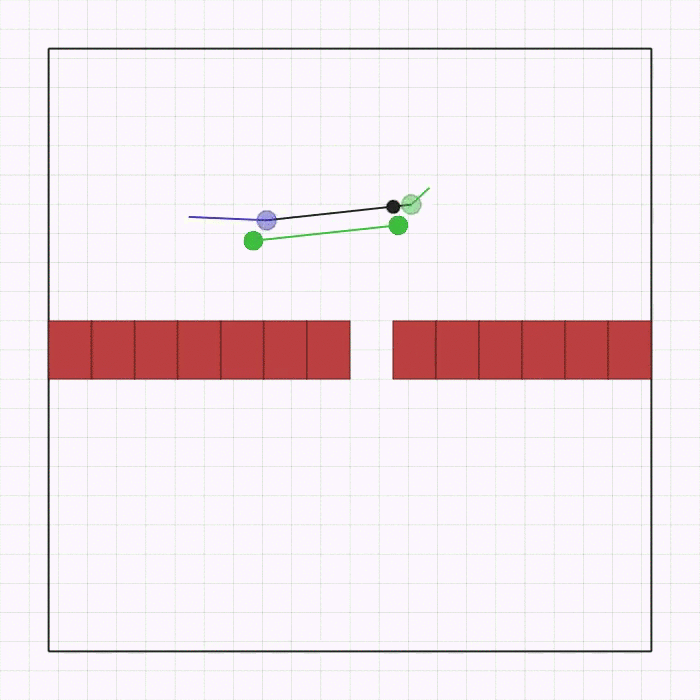ball_passage	ball_trajectory
buzz_wire	multi_give_way	navigation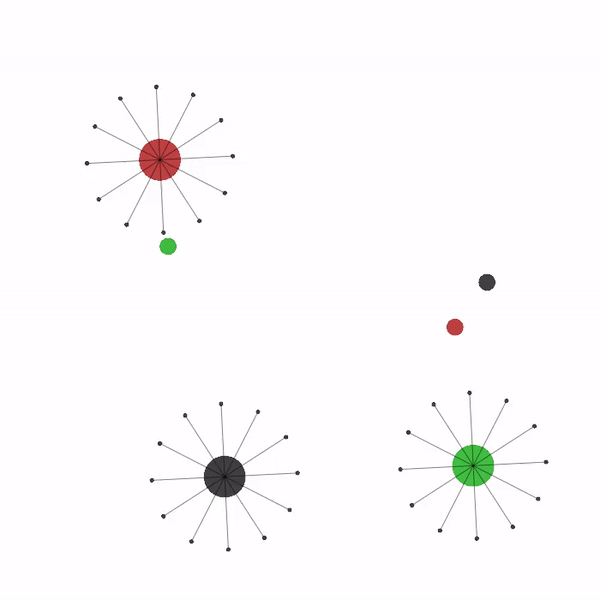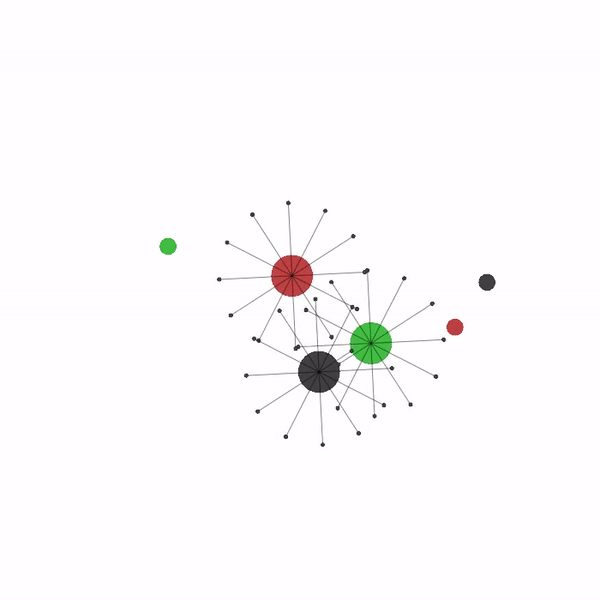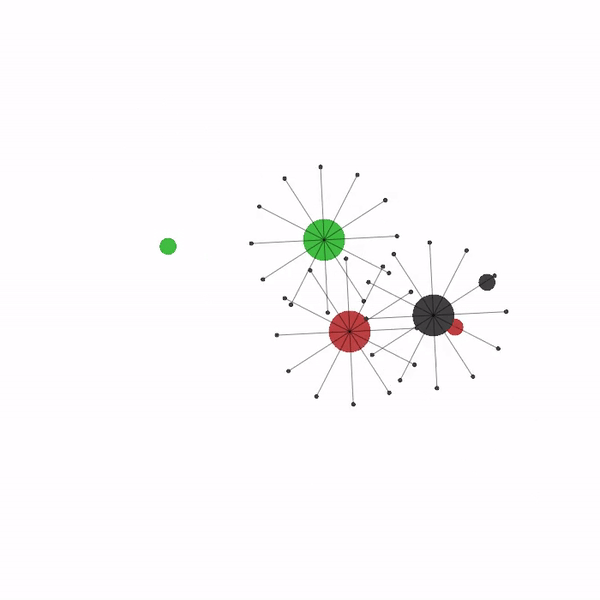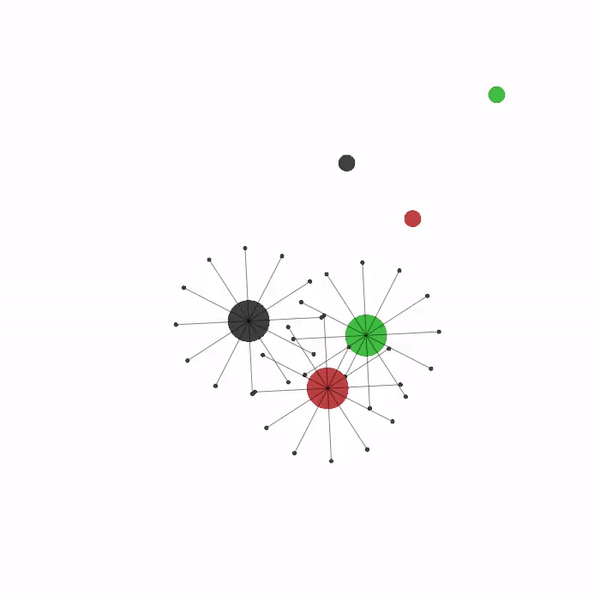
sampling	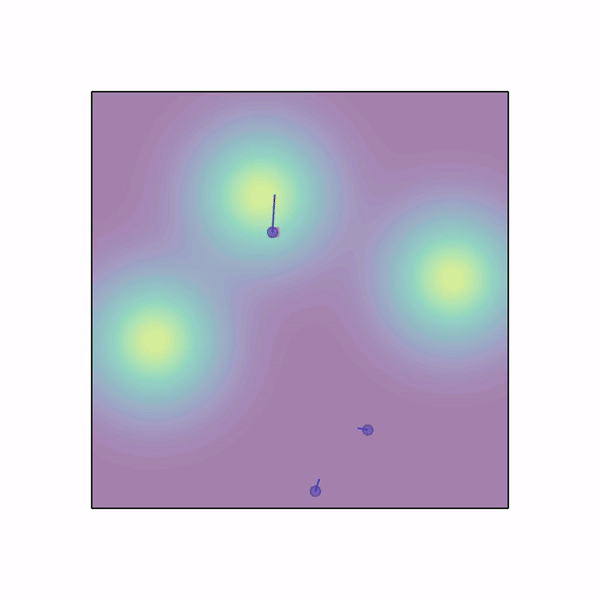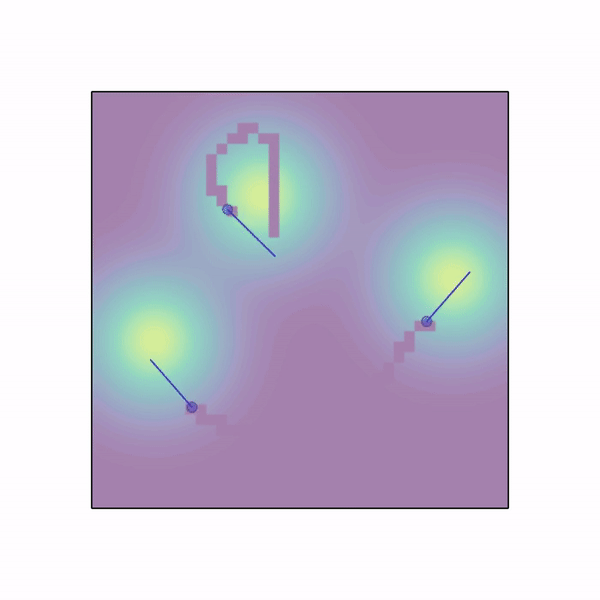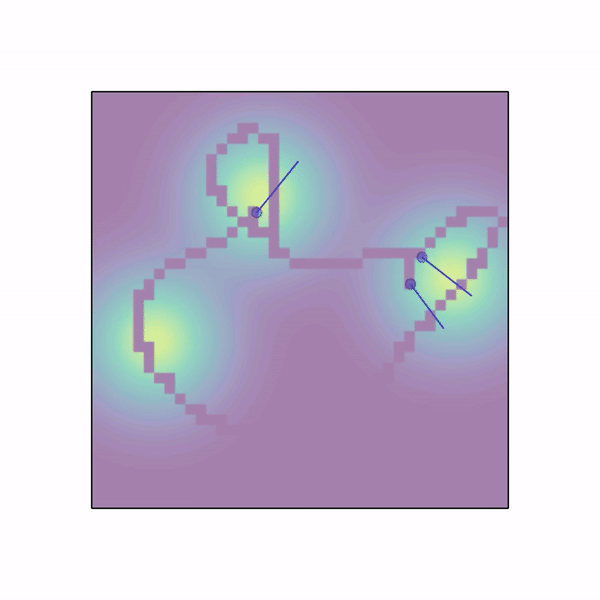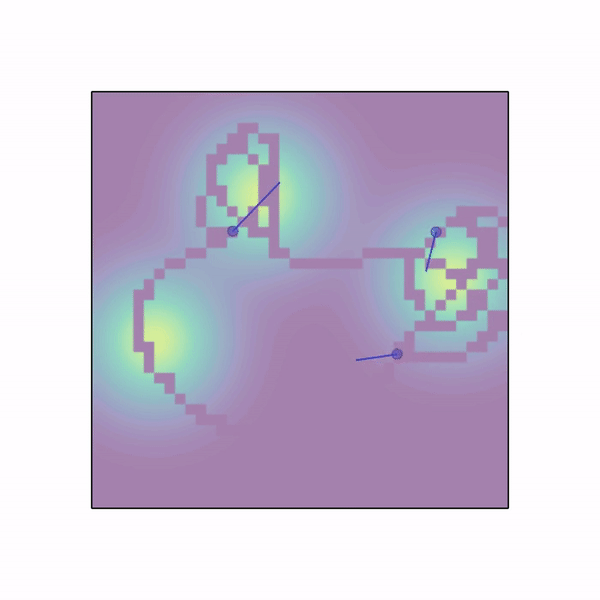wind_flocking	road_traffic

Main scenarios

Env name	Description	GIF
dropout.py	In this scenario, n_agents and a goal are spawned at random positions between -1 and 1. Agents cannot collide with each other and with the goal. The reward is shared among all agents. The team receives a reward of 1 when at least one agent reaches the goal. A penalty is given to the team proportional to the sum of the magnitude of actions of every agent. This penalises agents for moving. The impact of the energy reward can be tuned by setting energy_coeff. The default coefficient is 0.02 makes it so that for one agent it is always worth reaching the goal. The optimal policy consists in agents sending only the closest agent to the goal and thus saving as much energy as possible. Every agent observes its position, velocity, relative position to the goal and a flag that is set when someone reaches the goal. The environment terminates when when someone reaches the goal. To solve this environment, communication is needed.
dispersion.py	In this scenario, n_agents agents and goals are spawned. All agents spawn in [0,0] and goals spawn at random positions between -1 and 1. Agents cannot collide with each other and with the goals. Agents are tasked with reaching the goals. When a goal is reached, the team gets a reward of 1 if share_reward is true, otherwise the agents which reach that goal in the same step split the reward of 1. If penalise_by_time is true, every agent gets an additional reward of -0.01 at each step. The optimal policy is for agents to disperse and each tackle a different goal. This requires high coordination and diversity. Every agent observes its position and velocity. For every goal it also observes the relative position and a flag indicating if the goal has been already reached by someone or not. The environment terminates when all the goals are reached.
transport.py	In this scenario, n_agents, n_packages (default 1) and a goal are spawned at random positions between -1 and 1. Packages are boxes with package_mass mass (default 50 times agent mass) and package_width and package_length as sizes. The goal is for agents to push all packages to the goal. When all packages overlap with the goal, the scenario ends. Each agent receives the same reward which is proportional to the sum of the distance variations between the packages and the goal. In other words, pushing a package towards the goal will give a positive reward, while pushing it away, a negative one. Once a package overlaps with the goal, it becomes green and its contribution to the reward becomes 0. Each agent observes its position, velocity, relative position to packages, package velocities, relative positions between packages and the goal and a flag for each package indicating if it is on the goal. By default packages are very heavy and one agent is barely able to push them. Agents need to collaborate and push packages together to be able to move them faster.
reverse_transport.py	This is exactly the same of transport except with n_agents spawned inside a single package. All the rest is the same.
give_way.py	In this scenario, two agents and two goals are spawned in a narrow corridor. The agents need to reach the goal with their color. The agents are standing in front of each other's goal and thus need to swap places. In the middle of the corridor there is an asymmetric opening which fits one agent only. Therefore the optimal policy is for one agent to give way to the other. This requires heterogeneous behaviour. Each agent observes its position, velocity and the relative position to its goal. The scenario terminates when both agents reach their goals.
wheel.py	In this scenario, n_agents are spawned at random positions between -1 and 1. One line with line_length and line_mass is spawned in the middle. The line is constrained in the origin and can rotate. The goal of the agents is to make the absolute angular velocity of the line match desired_velocity. Therefore, it is not sufficient for the agents to all push in the extrema of the line, but they need to organize to achieve, and not exceed, the desired velocity. Each agent observes its position, velocity, the current angle of the line module pi, the absolute difference between the current angular velocity of the line and the desired one, and the relative position to the two line extrema. The reward is shared and it is the absolute difference between the current angular velocity of the line and the desired one.
balance.py	In this scenario, n_agents are spawned uniformly spaced out under a line upon which lies a spherical package of mass package_mass. The team and the line are spawned at a random X position at the bottom of the environment. The environment has vertical gravity. If random_package_pos_on_line is True (default), the relative X position of the package on the line is random. In the top half of the environment a goal is spawned. The agents have to carry the package to the goal. Each agent receives the same reward which is proportional to the distance variation between the package and the goal. In other words, getting the package closer to the goal will give a positive reward, while moving it away, a negative one. The team receives a negative reward of -10 for making the package or the line fall to the floor. The observations for each agent are: its position, velocity, relative position to the package, relative position to the line, relative position between package and goal, package velocity, line velocity, line angular velocity, and line rotation mod pi. The environment is done either when the package or the line fall or when the package touches the goal.
football.py	In this scenario, a team of n_blue_agents play football against a team of n_red_agents. The boolean parameters ai_blue_agents and ai_red_agents specify whether each team is controlled by action inputs or a programmed AI. Consequently, football can be treated as either a cooperative or competitive task. The reward in this scenario can be tuned with dense_reward_ratio, where a value of 0 denotes a fully sparse reward (1 for a goal scored, -1 for a goal conceded), and 1 denotes a fully dense reward (based on the the difference of the "attacking value" of each team, which considers the distance from the ball to the goal and the presence of open dribbling/shooting lanes to the goal). Every agent observes its position, velocity, relative position to the ball, and relative velocity to the ball. The episode terminates when one team scores a goal.
discovery.py	In this scenario, a team of n_agents has to coordinate to cover n_targets targets as quickly as possible while avoiding collisions. A target is considered covered if agents_per_target agents have approached a target at a distance of at least covering_range. After a target is covered, the agents_per_target each receive a reward and the target is respawned to a new random position. Agents receive a penalty if they collide with each other. Every agent observes its position, velocity, LIDAR range measurements to other agents and targets (independently). The episode terminates after a fixed number of time steps.
flocking.py	In this scenario, a team of n_agents has to flock around a target while staying together and maximising their velocity without colliding with each other and a number of n_obstacles obstacles. Agents are penalized for colliding with each other and with obstacles, and are rewarded for maximising velocity and minimising the span of the flock (cohesion). Every agent observes its position, velocity, and LIDAR range measurements to other agents. The episode terminates after a fixed number of time steps.
passage.py	In this scenario, a team of 5 robots is spawned in formation at a random location in the bottom part of the environment. A simular formation of goals is spawned at random in the top part. Each robot has to reach its corresponding goal. In the middle of the environment there is a wall with n_passages. Each passage is large enough to fit one robot at a time. Each agent receives a reward which is proportional to the distance variation between itself and the goal. In other words, getting closer to the goal will give a positive reward, while moving it away, a negative one. This reward will be shared in case shared_reward is true. If collisions among robots occur, each robot involved will get a reward of -10. Each agent observes: its position, velocity, relative position to the goal and relative position to the center of each passage. The environment terminates when all the robots reach their goal.
joint_passage_size.py	Here, two robots of different sizes (blue circles),connected by a linkage through two revolute joints, need to cross a passage while keeping the linkage parallel to it and then match the desired goal position (green circles) on the other side. The passage is comprised of a bigger and a smaller gap, which are spawned in a random position and order on the wall, but always at the same distance between each other. The team is spawned in a random order and position on the lower side with the linkage always perpendicular to the passage. The goal is spawned horizontally in a random position on the upper side. Each robot observes its velocity, relative position to each gap, and relative position to the goal center. The robots receive a shaped global reward that guides them to the goal without colliding with the passage.
joint_passage.py	This is the same as joint_passage_size.py with the difference that the robots are now physically identical, but the linkage has an asymmetric mass (black circle). The passage is a single gap, positioned randomly on the wall. The agents need to cross it while keeping the linkage perpendicular to the wall and avoiding collisions. The team and the goal are spawned in a random position, order, and rotation on opposite sides of the passage.
ball_passage.py	This is the same as joint_passage.py, except now the agents are not connected by linkages and need to push a ball through the passage. The reward is only dependent on the ball and it's shaped to guide it through the passage.
ball_trajectory.py	This is the same as circle_trajectory.py except the trajectory reward is now dependent on a ball object. Two agents need to drive the ball in a circular trajectory. If joints=True the agents are connected to the ball with linkages.
buzz_wire.py	Two agents are connected to a mass through linkages and need to play the Buzz Wire game in a straight corridor. Be careful not to touch the borders, or the episode ends!
multi_give_way.py	This scenario is an extension of give_way.py where four agents have to reach their goal by giving way to each other.
navigation.py	Randomly spawned agents need to navigate to their goal. Collisions can be turned on and agents can use LIDARs to avoid running into each other. Rewards can be shared or individual. Apart from position, velocity, and lidar readings, each agent can be set up to observe just the relative distance to its goal, or its relative distance to all goals (in this case the task needs heterogeneous behavior to be solved). The scenario can also be set up so that multiple agents share the same goal.
sampling.py	n_agents are spawned randomly in a workspace with an underlying gaussian density function composed of n_gaussians modes. Agents need to collect samples by moving in this field. The field is discretized to a grid and once an agent visits a cell its sample is collected without replacement and given as reward to the whole team (or just to the agent if shared_rew=False). Agents can use a lidar to sens each other. Apart from lidar, position and velocity observations, each agent observes the values of samples in the 3x3 grid around it.
wind_flocking.py	Two agents need to flock at a specified distance northwards. They are rewarded for their distance and the alignment of their velocity vectors to the reference. The scenario presents wind from north to south. The agents present physical heterogeneity: the smaller one has some aerodynamical properties and can shield the bigger one from wind, thus optimizing the flocking performance. Thus, the optimal solution to this task consists in the agents performing heterogeneous wind shielding. See the SND paper for more info.
road_traffic.py	This scenario provides a MARL benchmark for Connected and Automated Vehicles (CAVs) using a High-Definition (HD) map from the Cyber-Physical Mobility Lab (CPM Lab), an open-source testbed for CAVs. The map features an eight-lane intersection and a loop-shaped highway with multiple merge-in and -outs, offering a range of challenging traffic conditions. Forty loop-shaped reference paths are predefined, allowing for simulations with infinite durations. You can initialize up to 100 agents, with a default number of 20. In the event of collisions during training, the scenario reinitializes all agents, randomly assigning them new reference paths, initial positions, and speeds. This setup is designed to simulate the unpredictability of real-world driving. Besides, the observations are designed to promote sample efficiency and generalization (i.e., agents' ability to generalize to unseen scenarios). In addition, both ego view and bird's-eye view are implemented; partial observation is also supported to simulate partially observable Markov Decision Processes. See this paper for more info.

Debug scenarios

Env name	Description	GIF
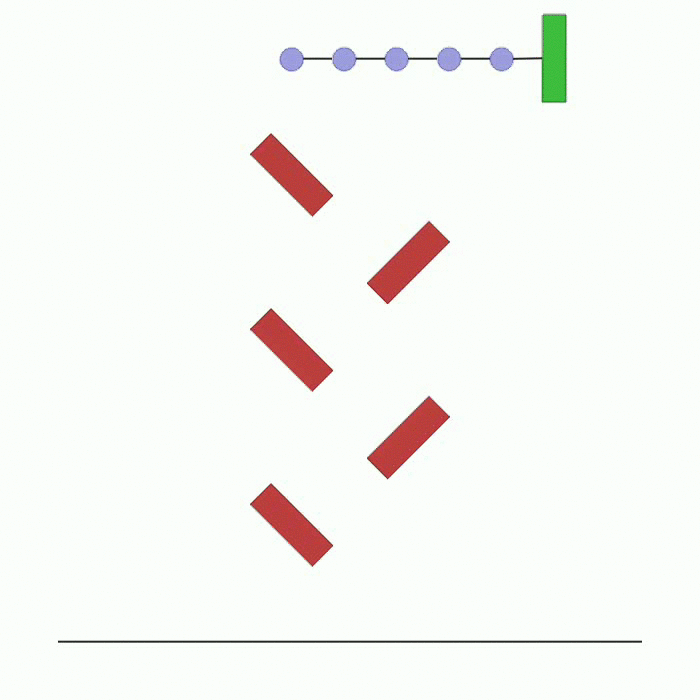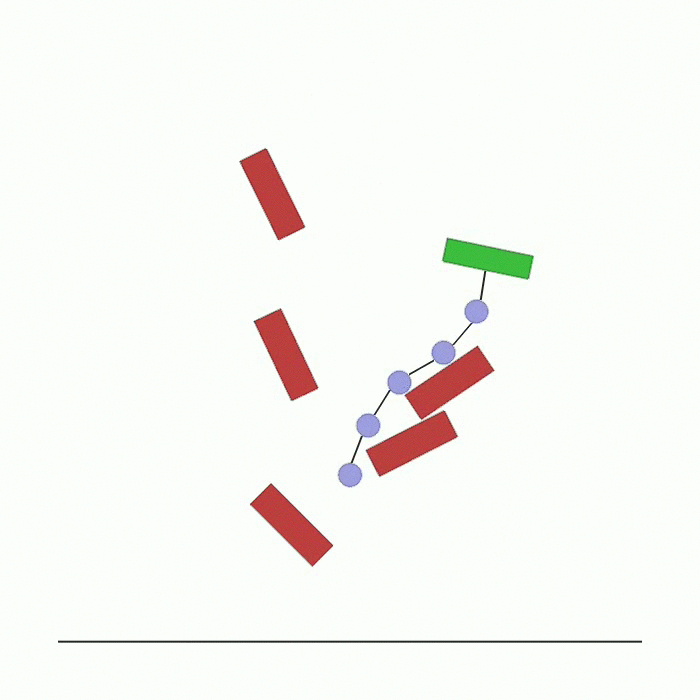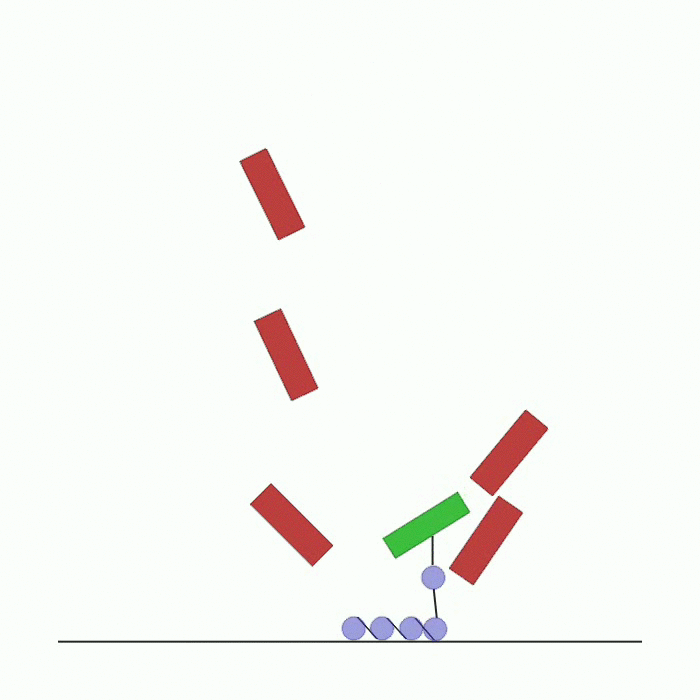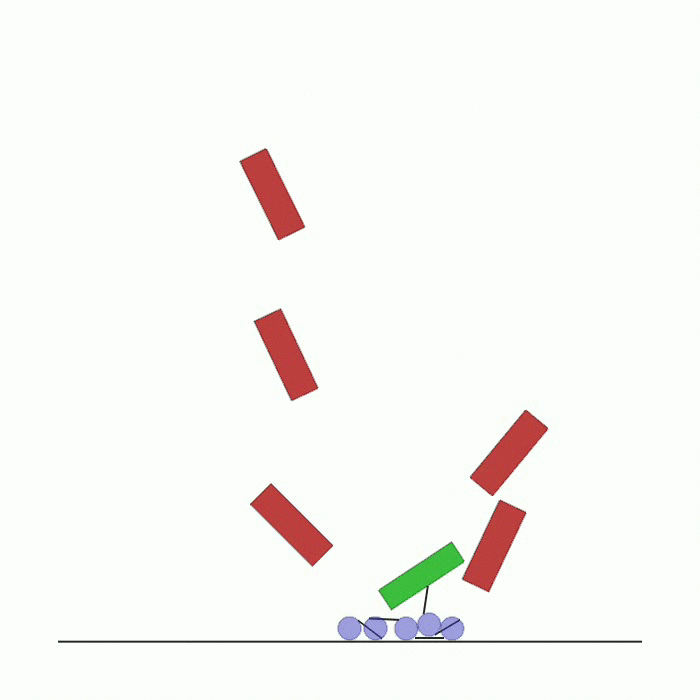
waterfall.py	n_agents agents are spawned in the top of the environment. They are all connected to each other through collidable linkages. The last agent is connected to a box. Each agent is rewarded based on how close it is to the center of the black line at the bottom. Agents have to reach the line and in doing so they might collide with each other and with boxes in the environment.
asym_joint.py	Two agents are connected by a linkage with an asymmetric mass. The agents are rewarded for bringing the linkage to a vertical position while consuming the least team energy possible.
vel_control.py	Example scenario where three agents have velocity controllers with different acceleration constraints
goal.py	An agent with a velocity controller is spawned at random in the workspace. It is rewarded for moving to a randomly initialised goal while consuming the least energy. The agent observes its velocity and the relative position to the goal.
het_mass.py	Two agents with different masses are spawned randomly in the workspace. They are rewarded for maximising the team maximum speed while minimizing the team energy expenditure. The optimal policy requires the heavy agent to stay still while the light agent moves at maximum speed.
line_trajectory.py	One agent is rewarded to move in a line trajectory.
circle_trajectory.py	One agent is rewarded to move in a circle trajectory at the desired_radius.
diff_drive.py	An example of the diff_drive dynamic model constraint. Both agents have rotational actions which can be controlled interactively. The first agent has differential drive dynamics. The second agent has standard vmas holonomic dynamics.
kinematic_bicycle.py	An example of kinematic_bicycle dynamic model constraint. Both agents have rotational actions which can be controlled interactively. The first agent has kinematic bicycle model dynamics. The second agent has standard vmas holonomic dynamics.
drone.py	An example of the drone dynamic model.

MPE

Our papers using VMAS

• VMAS features training of balance, transport, give_way, wheel
• HetGPPO features training of het_mass, give_way, joint_passage, joint_passage_size
• SND features training of navigation, joint_passage, joint_passage_size, wind
• TorchRL features training of navigation, sampling, balance
• BenchMARL features training of navigation, sampling, balance
• The Cambridge RoboMaster features training of navigation
• DiversityControl (DiCo) features training of navigation, sampling, dispersion, simple_tag

TODOS

TODOs are now listed here.

• [X] Improve test efficiency and add new tests
• [X] Implement 2D drone dynamics
• [X] Allow any number of actions
• [X] Improve VMAS performance
• [X] Dict obs support in torchrl
• [X] Make TextLine a Geom usable in a scenario
• [X] Notebook on how to use torch rl with vmas
• [X] Allow dict obs spaces and multidim obs
• [X] Talk about action preprocessing and velocity controller
• [X] New envs from joint project with their descriptions
• [X] Talk about navigation / multi_goal
• [X] Link video of experiments
• [X] Add LIDAR section
• [X] Implement LIDAR
• [X] Rewrite all MPE scenarios
  • [X] simple
  • [x] simple_adversary
  • [X] simple_crypto
  • [X] simple_push
  • [X] simple_reference
  • [X] simple_speaker_listener
  • [X] simple_spread
  • [X] simple_tag
  • [X] simple_world_comm